MATH1851 Ordinary differential equations
课程内容笔记，自用，不涉及任何 assignment，exam 答案
Notes for self-use, do not include any assignments or exams
MATH1851 的第二节：主要学习 常微分方程 ODE: Ordinary differential equation
常见 ODEs 的求解方法
-
常微分方程 Ordinary differential equation
微分方程 (Differential equation) 顾名思义，是含有函数微分的方程：即，其描述的是某一类函数与其导数之间的关系、
微分方程的解是一个函数
对于牛顿第二定律 \(F=mv\)，可以用微分方程进行表示 \(f(s)=m\frac{d^2 s}{ds^2}\)，未知数是 \(f(s)\)：一个关于 \(s\) 的函数，用来描述力
常 (ordinary) 微分方程是最简单的微分方程：即未知函数只含一个自变量 -
常微分方程的 Order
常微分方程的 order 是指方程中导数的最高次数
如对于 \(f(s)=f''(s)+c\)，这是一个 second order equation -
线性常微分方程 linear ODEs
微分方程可以分为线性常微分方程 (linear) 与非线性常微分方程 (non-linear)
一般来说，若因变量 (其他无关的变量可以是非线性的)都是线性的，则微分方程是线性的 (\(y^2, \log y, e^y, \sin y\) 这些都是非线性的因变量算子)
叠加原理 (Superposition Principle)：
若 ODE 的任意两个解相加仍然是 ODE 的解，则该 ODE 是 linear ODE
(判断 Order 与 linear 的一些例子)
-
微分方程的解的情况
ODE 的 order 越大，就越难得到确切解
非线性 ODE 求解很困难，甚至 impossible
First-Order linear ODE (一阶线性 ODE) 一定可解，通过 Integration Factor (积分因子) 解方程
具体方法是 \(\frac{d(\mathtt{expressions(x, y)})}{dx}=\) some functions of \(x\) alone
将微分方程整理成这种方式后，再对两边积分 \(\int\) -
积分因子法 Integration Factor
积分因子法适合解决 First order linear ODE
\(\frac{dy}{dx}+p(x)y=q(x)\)
(1) \(\frac{dy}{dx}\) 的系数 (coefficient) 是 \(1\)
(2) \(y\) 仅出现一次，且与 \(\frac{dx}{dy}\) 在方程的同一侧
在方程两边乘上积分因子 \(M(x)=e^{\int p(x)dx}\) 即可将左边化成 \(\frac{d(M(x)y)}{dx}\) 的形式
最后对方程两边求积分，整理后即可解出 \(y\)这里我们给出积分因子的推导：
\(y'+p(x)y=q(x)\)
两边同时乘上积分因子 \(M(x)\)：\(M(x)y'+p(x)M(x)y=q(x)M(x)\)
左边的形式很像导数的乘法，于是：\((M(x)y)'=q(x)M(x)\)
然而 \((M(x)y)'=M'(x)y+M(x)y'\)，对比可知 \(M'(x)=p(x)M(x)\)，即 \(\frac{M'(x)}{M(x)}=p(x)\)
这是个质数形式的微分方程：最后可得出 \(M(x)=\int p(x)dx\) -
伯努利方程 Bernoulli's equations (-> to linear ODE)
伯努利方程是一种特殊的 First order nonlinear equation：然而，我们可以将其转化为 first order linear equation 进行求解
伯努利方程的形式如下：\(\frac{dy}{dx}+p(x)y=q(x)y^n\)
可以看出，除了 \(q(x)\) 后有一个 \(y^n\) 外其余都与 First order linear ODE 没有区别
转化伯努利方程的方法是，将 \(y\) 换元为 \(w=y^{1-n}\)
\(dw=d(y^{1-n})=(1-n)y^{-n}dy\)
伯努利方程又可写为 \(\frac{dy}{dx}y^{-n}+p(x)y^{1-n}=q(x)\)，此时我们再将 \(w\) 与 \(dw\) 代入进行替换
得到 \(\frac{1}{1-n}\frac{dw}{dx}+p(x)w=q(x)\) -
Riccati's equations
Riccati 方程也是一种特殊的 First order nonlinear equation
Riccati 方程的形式如下: \(\frac{dy}{dx}=p(x)y^2+q(x)y+r(x)\)
若已知某特解 (particular solution) \(Y(x)\)，我们令 \(y=Y-\frac{1}{u}\)
可以列出以下两方程:
\(Y'=p(x)Y^2+q(x)Y+r(x)\)
\(y'=Y'+(-\frac{1}{u^2})\frac{du}{dx}\)
将两方程代入原式 \(y'=p(x)y^2+q(x)y+r(x)\) 经过变换得到 first order linear equation:
\(u'+(2pY+q)u=-p\) -
Separable equations
Separable equations 指的是形如 \(\frac{dy}{dx}=X(x)Y(y)\) 的 first order equations
Separable 的含义是，可以将方程整理成这样的形式 \(\frac{dy}{Y(y)}=X(x)dx\)
再对两边进行积分 \(\int \frac{1}{Y(y)}dy=\int X(x)dx\)，这样就可以解出微分方程 -
Homogeneous equations 齐次方程 (-> to separable equations)
若方程可以化为这样一种形式：除 \(\frac{dx}{dy}\) 外，所有项都能化成 \(c\frac{y}{x}\) 的形式，那么该微分方程是一个 homogenous equation
(常数\(=c(\frac{y}{x})^0\), \(\frac{x}{y}=(\frac{y}{x})^{-1}\)，这些都可以用 \(c\frac{y}{x}\) 进行表示)
齐次方程的解法：令 \(w=\frac{y}{x}\) 并将用 \(w\) 对方程进行换元 (substitute \(y\) by \(w\))，最后能得到一个 separable equation
按 separable 方程的方法求解之后代回 \(y\) 即可上面对 homogeneous equations 的定义是非正式的实用形式，下面补充以下 homogeneous equations 的正式定义
对于一个度数为 \(N\) 的 homogeneous function \(f\)，我们有 \(f(kx, ky)=k^{N} f(x,y)\) (例，\(x^2+3xy+y^2\) 就是一个 homogeneous function)
homogeneous equation 表现为该形式 \(\frac{dy}{dx}=f(x, y)\), 其中 \(f\) 是一个 homogeneous function
求解 Exact ODEs
-
Partial Derivatives 偏导数
对于一个含有两个以上 independent variables 的函数 \(F\)
求 \(\frac{\partial F}{\partial x}\) \(F\) 对变量 \(x\) 的偏导时，将除了 \(x\) 以外的变量视为常数
例：对于 \(F(x,y)=x^2 y\)，\(\frac{\partial F}{\partial x}=2xy\)，而 \(\frac{\partial F}{\partial y}=x^2\)
\(F\) 的 total differential 全微分等于分别对所有变量分别求偏导的和，即：
\(dF=\frac{\partial F}{\partial x}dx+\frac{\partial F}{\partial y}dy+...\) (很好理解，总 \(F\) 的微小变化量 \(=\) 在各个方向上的微小变化量之和)
注意，\(F\) 先对 \(x\) 求偏导再对 \(y\) 求偏导的结果与先对 \(y\) 求偏导再对 \(x\) 求偏导的结果是一样的 (mixed partial derivatives 与顺序无关) -
Exact ODEs 全微分方程式
我们说一个 ODE 是 exact 的，代表其能写成 exact differential 的形式：
对于 \(M(x,y)dx+N(x,y)dy=0\)
若存在一个 scalar function \(F\) 使得 \(\frac{\partial F}{\partial x}=M\) 且 \(\frac{\partial F}{\partial y}=N\)
则 ODE 可以写成这种形式：\(\frac{\partial F}{\partial x}dx+\frac{\partial F}{\partial y}dy=0\) 即 \(dF=0\)，\(F=\mathtt{constant}\)
这样的 ODEs 被称为 exact ODEs(注意，在解 ODEs 时，我们将 \(y\) 视为 \(x\) 的 implicit function；而在判断 exact ODEs 时，我们又将 \(y\) 与 \(x\) 视为 independent variable)
-
全微分方程式的判断
对于 ODE \(M(x,y)dx+N(x,y)dy=0\)
若 ODE 是 exact 的，则存在 \(\frac{\partial F}{\partial x}=M(x,y), \frac{\partial F}{\partial y}=N(x,y)\)
由于交换偏导顺序不影响求偏导结果，则有 \(\frac{\partial}{\partial x}\frac{\partial F}{\partial y}=\frac{\partial}{\partial y}\frac{\partial F}{\partial x}\)，即
\(\partial(M)/\partial y=\partial (N)/\partial x\) (重要！！！)
对于不 exact 的方程 \(M(x,y)dx+N(x,y)dy=0\)，有可能找到一个 multiplicative factor \(\epsilon(x,y)\) 使得 \(\epsilon(x,y)M(x,y)dx+\epsilon(x,y)N(x,y)dy=0\) 是全微分方程
这个 multiplicative factor 可通过计算式子 \(\partial (\epsilon(x,y)M)/\partial y=\partial (\epsilon(x,y)N)/\partial x\) 得出
-
求解 Exact ODEs
当题目要求解一个形如 \(M(x)dx+N(x)dy=0\) 的 ODE 时，我们猜测其为 Exact ODEs 并按照以下方式求解
(1) 判断方程是否满足 \(\partial (M)/\partial y=\partial (N)/\partial x\)，若满足，证明其为 exact ODE
(2) 计算 \(F=\int M(x,y)dx+g_1(y)\)，其中 \(g_1(y)\) 代表任意与 \(y\) 相关的函数
(3) 计算 \(F=\int N(x,y)dy+g_2(x)\)，其中 \(g_2(x)\) 代表任意与 \(x\) 相关的函数
(4) 对比两式，得到一个同时满足该两个式子的结果 \(F\) (\(F\) 中不应再含有 \(g_1(y)\) 与 \(g_2(x)\))
(5) 此时我们将 Exact ODE 的解转化为了隐函数 \(F\) 在 \(F=c\) 时的结果，将 \(F=c\) 整理后即可得到原 exact ODE 的解
高阶齐次 ODE 的解: Homogeneous Higher-Order ODEs
-
Linear Independence 线性无关
对于二阶 ODE \(y''-y'=0\)，我们有解 \(y=e^x\) 与 \(y=2e^x\) 与 \(y=e^{-x}\)
然而，这两个解很明显是等价的，我们只需要留下其中一个
而 \(y=e^x\) 与 \(y=e^{-x}\) 则是不等价的解
我们将 "等价" 定义为 线性相关 (linearly dependent)，"不等价" 定义为 线性无关 (linearly independent)
若两个解 \(y_1, y_2\) 是线性相关的，则 \(\alpha y_1+\beta y_2=0\) 存在非平凡解 (\(\alpha, \beta\) 不是全 \(0\))；若其是线性无关的，则 \(\alpha y_1+\beta y_2=0\) 仅有在 \(\alpha=\beta=0\) 时成立 -
Wronskian determinant 朗斯基行列式
引入 Weonskian determinant 来快速判断 \(n\) 个函数 \(u_1(x), u_2(x), ..., u_n(x)\) 的线性相关性- 对于 \(n=2\)，即对于 \(u(x), v(x)\)
若对于所有 \(x\)，都有 \(u(x)v'(x)-u'(x)v(x)=0\) (这是 \(2\) 阶朗斯基行列式的展开)
则 \(u(x), v(x)\) 是 linearly dependent 的 (这是充要条件 sufficient condition) - 对于 \(n>2\)，我们计算朗斯基行列式 \(W[u_1, u_2,..., u_n](x)\)
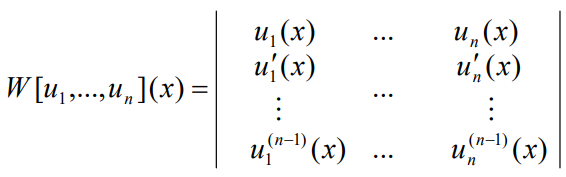
若对于所有 \(x\)，\(W=0\)，则 \(\{u_1,u_2,...,u_n\}\) 是 linearly dependent 的
- 对于 \(n=2\)，即对于 \(u(x), v(x)\)
-
常数系数的二阶齐次线性 ODEs (Homogeneous second-order linear equations with constant coefficients)
注意，这里的 homogeneous 含义与之前的 homogeneous function 有不同！！！
对于形如 \(y''+a_1 y'+a_2 y=0\) 且 \(a_1, a_2\) 均为常数的微分方程，我们称其为 homogeneous second-order linear ODE with constant coefficient- Linear 线性：\(y''\) 项的系数是 \(0\)
- Homogeneous 齐次：等式右边是 \(0\)；除了 \(y'',y',y\) 之外的项数均是 \(0\)
- With constant coefficients: \(a_1, a_2\) 均为常数
对于这一类微分方程，我们采用解特征方程 (characteristic equation)的方法进行求解
-
特征方程 characteristic equations
令 \(y=e^{\lambda x}\)，可求出方程 \(y''+a_1 y'+a_2 y=0\) 的特征方程 (characteristic/polynomial) \(\lambda^2+a_1 \lambda+a_2=0\)
解得 \(\lambda\) 之后，我们求 \(y\) 的通解 (显然，若 \(\lambda\) 存在，\(y\) 有无数个解：对于任意 \(C\)，\(Ce^{\lambda x}\) 都是一个解)- 特征方程有两实根 (distinct real roots) \(m,n \ (m\neq n)\)
\(y\) 的通解为 \(y=C_1 e^{mx}+C_2 e^{nx}\) - 特征方程有重根 (repeated roots) \(m\)
\(y\) 的通解为 \(y=C_1 e^{mx}+C_2 xe^{nx}\) (这个结果有点反直觉，我们用 reduction of order 进行证明，见下例证 \(1\))
Reduction of Order (降次法)：若已知 ODE 的一个解，则其 order 能 reduce 1
具体来说，求出一个已知解后，我们令 \(y=(\mathtt{known \ solution})u\) 且定义 \(w=u'\)，即可得到一个关于 \(w\) 的降 \(1\) 次 ODE - 复数根 (complex roots)
一元二次方程若 \(\Delta <0\)，则会产生一对共轭虚根 (conjugate pair) \(a+bi, a-bi\). 这是公式 \((\frac{-b\pm \sqrt{\Delta}}{2a}\) 这里的 \(a,b\) 指的是特征方程中的系数)
\(y\) 的通解为 \(y=C_1 e^{(a+bi)x}+C_2 e^{(a-bi)x}\)
或写成这种形式 \(y=e^{ax}(A\cos bx+B\sin bx)\)，其中 \(A=C_1+C_2, B=i(C_1-C_2)\) (利用欧拉公式 \(e^{ix}=\cos x +i\sin x\)，见下证明 \(2\))
证明 \(1\) (重根时的通解):
关于 Reduction of Order (这是一个拟设 (ansatz)):
对于二阶 ODE，在已知一个解 \(y_1(x)\) 的情况下，通过 Reduction of Order \(u=y/y_1\) 能够生成另一个线性无关的解 \(y_2(x)\). 对于 \(n\) 阶 ODE，在已知一个解的情况下，通过 Reduction of Order \(u=y/y_1\) 能够得到一个 关于 \(u\) 的 \((n-1)\) 阶的 ODE 实现降阶
这建立在方程的通解 \(y\) 一定能表示成某特解 \(y_1(x)\) 与某个函数 \(u(x)\) 之积的形式 \(y=y_1(x)u(x)\)
证明 \(2\) (虚根通解的三角函数写法):
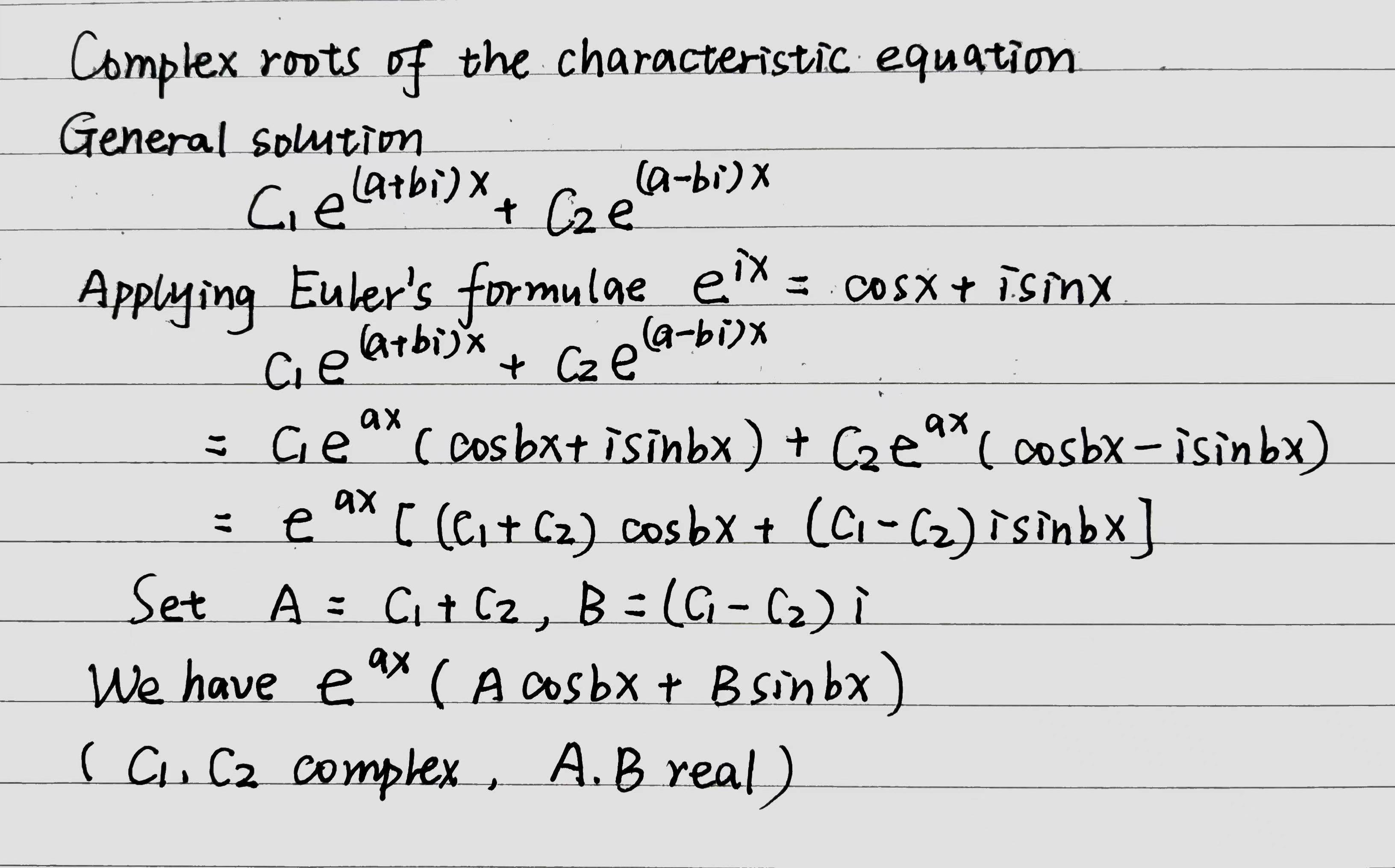
注意，\(C_1,C_2\) 是复数，而 \(A,B\) 是实数 - 特征方程有两实根 (distinct real roots) \(m,n \ (m\neq n)\)
-
Expansion to homogeneous higher-order equations & repeated complex roots
高阶齐次 ODE 的特征方程解基本上是以上三种情况的复合；对于每一种情况采用对应的解法即可，较为直接
但是，这一种情况比较特殊，那就是重\(\cdot\)复数根 (repeated complex roots)，这种情况是不可能在二阶特征方程里出现的 (二阶特征方程涉及复数根一定是一对共轭复数)
对于解 \(a+bi, a+bi, a-bi, a-bi\)，我们有 \(y\) 的通解为
\(y=Ae^{(a+bi)x}+Be^{(a-bi)x}+Cxe^{(a+bi)x}+Dxe^{(a-bi)x}\)
即 \(y=e^{(a+bi)x}(A+Cx)+e^{(a-bi)x}(B+Dx)\)
或 \(y=e^{ax}[A\cos bx+b\sin bx+x(C\cos bx+D\sin bx)]\) -
Application to the simple harmonic oscillator: Free oscillation
自由震荡 (free oscillation) 指的是这样一个物理模型：质量为 \(m\) 的物体连接着系数为 \(k\) 的弹簧
阻尼 (damping) 与速度成比例 \(c\); 根据牛顿运动定律有
\(m \frac{d^2 x}{dt^2}=-kx-c\frac{dx}{dt}\)
可以发现这是一个二阶 ODE：\(mx''+cx'+kx=0\)
其特征方程为 \(m\lambda^2+c\lambda+k=0\)，根可以表示为 \(\lambda = (-c \pm \sqrt{c^2-4mk})/2a\)- 若 \(c^2<4mk\)
此时的 free oscillation 被称为 underdamped vibration (小于，所以是 underdamped)
ODE 有两复数解 - 若 \(c^2=4mk\)
此时的 free oscillation 被称为 critically damped vibration (等于，所以是 critically damped)
ODE 有重根 - 若 \(c^2>4mk\)
此时的 free oscillation 被称为 overdamped vibration (大于，所以是 overdamped)
ODE 有 distinct 的两实根
- 若 \(c^2<4mk\)
-
Cauchy-Euler Equations
Cauchy-Euler Equations 是一种特殊的微分方程，同样使用特征方程法求解
与二阶齐次线性 ODE 的特征方程不同，我们使用 \(y=x^\lambda\) 而不是 \(y=e^{\lambda x}\) 来进行转换
Cauchy-Euler 方程的形式如下：
\(x^n y^{(n)}+c_1 x^{n-1}y^{(n-1)}+...+c_{n-1}xy'+c_n y=0\)- \(x\) 的指数与 \(y\) 的导数阶数相同
- \(c_1,c_2,...,c_n\) 是常数，但是第一项 \(x^n y^{(n)}\) 的系数是 \(1\)
对于 \(x^n y^{(n)}\)，我们代入 \(y=x^{\lambda}\) 得到的特征方程项是 \(\lambda (\lambda-1)...(\lambda-n)x^{\lambda}\) ("compensate" for the loss of exponent)
接下来我们研究二阶的 Cauchy-Euler Equation 的特征方程 \(x^2y''+c_1 xy'+c_2\)
代入 \(y=x^{\lambda}\)，可得到特征方程 \(\lambda^2+(c_1-1)\lambda+c_2=0\)- \(\Delta>0\)
此时特征方程有两 distinct 实根 \(\lambda_1\) 与 \(\lambda_2\)
方程的通解为 \(Ax^{\lambda_1}+Bx^{\lambda_2}\) - \(\Delta=0\)
此时特征方程有重根 \(\lambda_1\) 与 \(\lambda_1\)
方程的通解为 \(Ax^{\lambda_1}+B\ln x x^{\lambda_1}\) (联想二阶 ODE 特征方程重根解情况 \(Ae^{\lambda x}+Bxe^{\lambda x}\)) - \(\Delta<0\)
此时特征方程有复数根 \(\lambda =\alpha\pm\beta i\)
方程的通解为 \(Ax^{\alpha+\beta i}+Bx^{\alpha-\beta i}\)
利用欧拉公式，我们化简 \(x^{\beta i}=e^{\ln x^{\beta i}}=e^{(\beta \ln x)i}=\cos(\beta \ln x)+i\sin (\beta \ln x)\)
方程的通解也可写成 \(x^{\alpha}(Ax^{\beta i}+Bx^{-\beta i})=x^{\alpha}[(A+B)\cos(\beta \ln x)+(A-B)\sin (\beta \ln x)]=x^{\alpha}(C\cos(\beta \ln x)+D\sin(\beta \ln x))\)
多重根(例 \(3\) 个): \(\lambda, \lambda, \lambda\)，\(C_1 x^{\lambda}+C_2 (\ln x) x^{\lambda}+C_3 (\ln x)^2 x^{\lambda}\)
Inhomogeneous equations with constant coefficients
之前我们讨论的 homogeneous 指的是：除与 \(y\) 有关的项 (例，\(y, y', y''...\)) 之外都是 \(0\)
这里我们来解 inhomogeneous equations：是更 general 的状况
(简单判断的方法：homogeneous \(\to\) 等式右边为 \(0\)，inhomogeneous \(\to\) 等式右边非 \(0\))
以二阶 inhomogeneous equations 为例: \(y''+a_1 y'+a_2 y=f(x)\)
-
解 Inhomogeneous 的基本原则 (重要!!!)
inhomogeneous equations 的通解:
General Solution \(=\) Complementary Function (CF) \(+\) Particular Solution/Integral (PS/PI)
补充方程 (CF) 指的是对应的 homogeneous equation 的解；本质上是任意两解间的差
下面，我们以一个例子来进行说明：
对于 inhomogeneous equation \(y''+k^2 y=f(x)\neq 0\)，有两个解 \(y_1, y_2\)，因此
\(y_1''+k^2 y_1=f(x)\)
\(y_2''+k^2 y_2=f(x)\)
两式相减有 \((y_1''-y_2'')+k^2(y_1-y_2)=0\)
补充函数 Complementary Function \(y_c=y_1-y_2\)，因此 \(y_c''+k^2 y_c=0\) (所以可以看出 \(y_c\) 是两解之间的差且是对应 homogeneous 的解)
因此该方程的任何一个解都能这样表达 \(y=y_c+y_1\) (例: y_2=y_c+y_1) -
找特解: 待定系数法 undetermined coefficient
实际上是进行一个 educated guess，可以用来获得简单的特解
对于等式右边的 inhomogeneous terms，每一项所对应的特解可以这样猜测
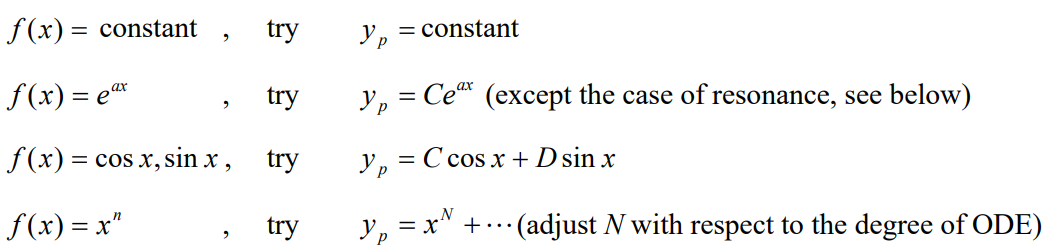
注意，我们猜测的特解的项中若与补充函数有重合，则那些项可舍弃
(解释一下 \(x^n\) 项：若该方程为 \(N\) 阶 ODE，则特解可猜测为 \(C_1 x^N+C_2 x^{N-1}+...C_N x\))
若等式的右边十分复杂，无法看出特解，我们将采用 variation of parameter 方法 (下面会介绍) -
Special case: Resonance 共振
解 inhomogeneous equation 时，当我们发现 inhomogeneous term (非齐次项，即方程的右边) 与补充函数 CF 产生了重合 (overlapping) 时，需要采取其他方法来找特解
(即，对于 \(y''+a_1 y'+a_2 y=f(x)\)，等式右边的 \(f(x)\) 是 homogeneous equation \(y''+a_1 y'+a_2 y=0\) 的解)
例：对于 inhomogeneous equation \(y''-3y'+2y=e^x\)，我们尝试采用传统的找特解方法
令 \(y=\lambda e^x\)，代入得 \(\lambda e^x-3\lambda e^x+2\lambda e^x=e^x\)，化简后有 \(e^x=0\)，这明显不成立
出现这种情况的原因是 \(e^x\) 本身就是 \(y''-3y'+2y=0\) 的一个解，产生了 resonance- Try another guess
我们对传统的猜特解进行修改：当 \(\lambda e^x\) 不能作为等式右边为 \(e^x\) 的特解时，我们尝试 \(\lambda xe^x\) - D operator method
对于存在共振的 inhomogeneous equation，我们可以采用 D operator method 寻找特解
D operator 指的是令 \(D=\frac{d}{dx}\) 并将 \(D\) 视作一个数
任意一个 homogeneous term \(a_n y^{(n)}\)，都可以用 \(D\) 来表达：\(a_n y^{(n)}=a_n \frac{d^n y}{dx^n}=a_n (\frac{d}{dx})^n y =a_n D^n y\)
我们也可以通过 D operator 来快速找到一个 homogeneous equation 的特征方程：例，对于 \(y''-3y'+2y=0\)，可以写成 \((D^2-3D+2)y=0\)，从而得到特征方程 \(\lambda^2-3\lambda+2=0\)
接下来，我们通过例子 \(y''-3y'+2y=e^x\) 来说明如何用 D operator 找到 inhomogeneous equation 的特解
重要：找到一个仅含有 \(D\) 与 inhomogeneous term 的式子来摧毁 (destroy) 等式的右侧: \((e^x)'-e^x=0\) 所以 \((D-1)e^x=0\)
又 \((D^2-3D+2)y=e^x\)
我们利用之前得到的式子"摧毁" \(e^x\)，将等式右边变为 \(0\): \((D^2-3D+2)(D-1)y=(D-1)e^x=0\)
由此，我们得到了一个关于 \(y\) 的新的 homogeneous equation，并且其特征方程就是 \(y\) 的系数 \((\lambda^2-3\lambda +2)(\lambda -1)=0\)
该方程有根 \(1, 1, 2\)，对应解 \(C_1 e^x, C_2 xe^x, C_3 e^{2x}\) 其中新 (NEW!!，即非 CF 的部分) 的解可以作为原 inhomogeneous equation 的特解 (这里是 \(C_2 xe^x\)) - Variation of Parameter 参数变换法
这是解 inhomogeneous ODE 最 general 的方法，本质上也是一种 Reduction of Order!
对于 inhomogeneous ODE \(y''+p(x)y'+q(x)y=f(x)\)，我们先求出其 homogeneous form 的两个解 \(y_1, y_2\) (即，\(C_1 y_1+C_2 y_2\) 是补充函数 CF)
Variation of Parameter 建立在方程的某个特解 \(y_p\) 一定能表示成 \(u_1(x) y_1(x)+u_2(x)y_2(x)\) 的假设上
我们求 \(y_p=u_1(x) y_1(x)+u_2(x)y_2(x)\) 的一阶导 \(y_p'\) 与二阶导 \(y_p''\) 并代入 \(y''+p(x)y'+q(x)y=f(x)\)
在求导过程中，为了不让情况变得更加复杂，我们令 \(u_1'(x)y_1(x)+u_2(x)'y_2(x)=0\) (不然最后的式子里会出现 \(u_1''\) 与 \(u_2''\))
最后我们会得到两个关于 \(u_1'(x)\) 与 \(u_2'(x)\) 的方程，分别是:
\(u_1'(x)y_1(x)+u_2'(x)y_2(x)=0, u_1'(x)y_1'(x)+u_2'(x)y_2'(x)=f(x)\)，解出 \(u_1'(x), u_2'(x)\) 积分后即可得到 \(u_1(x), u_2(x)\)
Tutorial Examples:
下面是一个用 D operator method 与 variation of parameter 解 inhomogeneous equations 的例子 (btw, tutorial 真的比 lecture 有用一万倍)
- Try another guess
