ENGG1310 P2.2 Data, Logic Gates & Binary Computation
课程内容笔记,自用,不涉及任何 assignment,exam 答案
Notes for self-use, do not include any assignments or exams
Data Representations
这里可以和前面介绍的数字信号/模拟信号进行联系
在这里我们将介绍数据的两种表征方式 (data representation): Analogue (模拟) 与 Digital (数字)
-
Analog Data
Analog Data 在时间轴上取值连续 (continuous)

现实生活中的大部分数据,例如气压,亮度,湿度,温度等等,都是 analog 的
Analog System 可以储存或处理 Analog Data -
Digital Data
Digital Data 在时间轴上取值离散 (discrete),且在不同的时间单元上取值不同
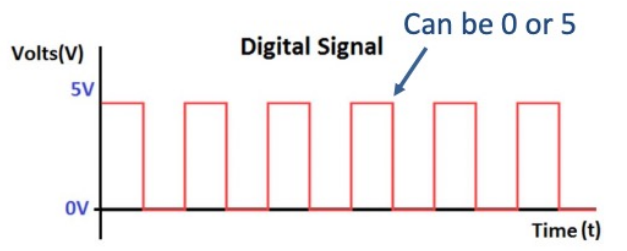
在电脑内部进行存储与处理的数据几乎都是 Digital Data (更具体的说,是 Binary Data) -
Digital Abstraction
Digital Abstraction 将所有的信号抽象成两个离散值 (2 discrete values),一般是 (True/False)
这样的好处是



-
Analog-to-Digital Conversion
实际中的数据大多是 Analog 的,然而电脑只能处理 Digital 的数据
为了令电脑能储存并处理 Analog 的数据,我们需要将 Analog Data 转为 Digital Data
我们通过 Sampling 与 Quantization 来实现这个过程
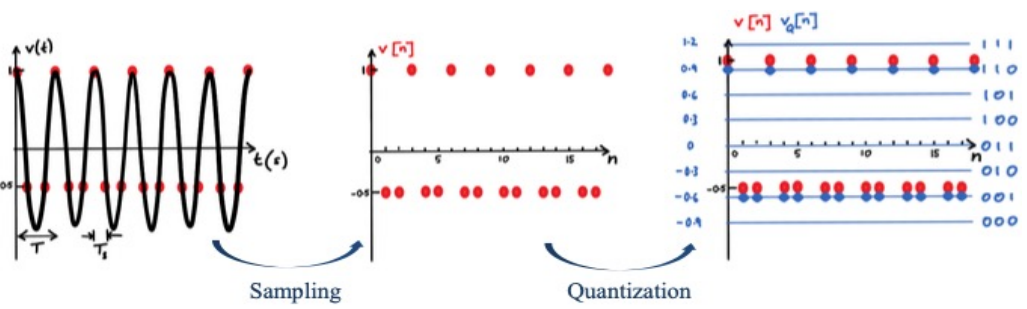
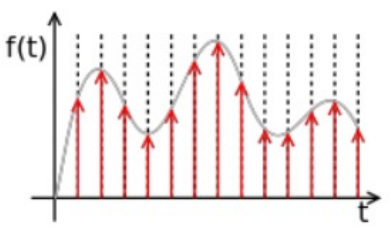
Sampling 是指,recording an analog signal at regular discrete units of time (例如,每 秒记录一次)
Quantization 是指,将所有的 analogue value 映射到一个有限的 digital value set 中去 -
Analog-to-Digital Converter (ADC)
一个能够对 Analog Data 进行 Sampling 与 Quantization,并将其转化为 Digital Data 的装置,被称为 Analog-to-Digital Converter (ADC)
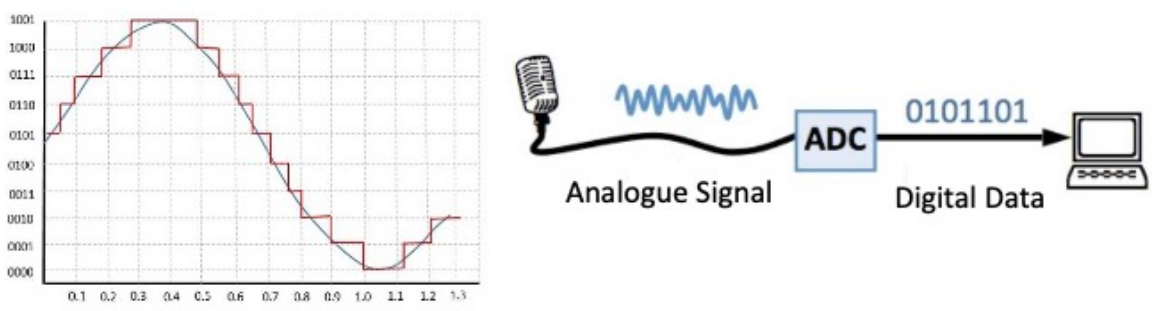
1-bit ADC 将 Analog Data 转化为 Binary Data
ADC 将决定 Binary Data 所代表的- logical states:例如 代表 高/低,冷/热,关/开
- output voltage:在实际的电路设计中, 将被两个不同的电压表示,一般来说, 与 的代表电压分别是 minimum/maximum allowable voltage

在 Analog-to-Digital 的转化过程中,无论是 sampling 还是 quantization 都会造成信息的错误与丢失 (errors & loss of information)
转换之后的信息与原信息的差异被称为 quantization error/noise (量化错误/量化噪声)
虽然 ADC 会导致 loss of information,但是 digital data processing 有其独特的优越性



-
Digital-to-Analog Converter (DAC)
DAC 将 Digital Data 转化为有着连续物理性质的 Analog Data
例如耳机:其接收到的数据是 Digital Data,但输出的是表现为 Analog Data 的声音
Binary Computation
-
Binary Representation
二进制数据 Binary Data 由若干个 与 表示:这些数字也被称为 比特 (bits) (bits 是 binary digits 的缩写)
binary/logic value 被 low voltage 所代表 ( 或接地)
binary/logic value 被 high voltage 所代表 () -
Binary Digits: Bits
一个二进制数 binary digits 被称为 比特 bits,它是电脑系统中最基础的信息单元
一个比特只能代表 ,其所对应的 electrical status 是开或者关 -
Binary numbers
binary numbers (二进制数) 以 比特串 (bit-string) 的形式表示
文本,图像这些数据类型均可用比特串进行表示,之后在计算机中进行存储与处理
一个长度为 的比特串可以表示 个不同的值
所有现代计算机均 work on binary numbers of data -
Binary Coding 二进制编码
一个二进制编码方案必须满足以下要求- Uniqueness:不同的值必须被不同的二进制编码表示
- Standardization:二进制编码方案必须是标准化的,这样才能在不同的环境下进行应用
- Compatibility
-
Representation of Decimal Numbers
公式
其中 被称为 base number,迭代的 被称为 的 position number,这种表达方式被称为 positional-value (PV) system
由 least significant digit (最右侧) 迭代到 most significant digit
任意 进制的数转换为十进制都遵循这一规律 -
Decimal to Binary/Hex
短除法,在 remainder < base 条件下结束
通过短除法得到的结果:所有的 remainder 由下至上写出来 -
Binary Hexadecinal
二进制数和十六进制数之间的转换遵循这样的规则:
由右到左 (即从 least significat digit 到 most significant digit) 分解,
若二进制转十六进制,则 四位一组,并将这四位二进制数写成对应的一位十六进制数 (若到左端的 MSD 凑不到四个,则补上前缀 )
若十六进制转二进制,则逐位将一位十六进制数写成对应的二进制数
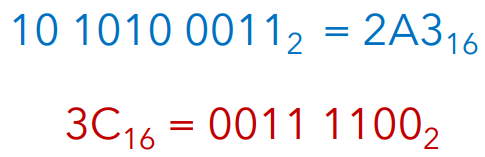
Number representation
感觉是这堂课中为数不多的干货内容,,,趁着机会好好了解下二进制数的负数表达
-
Unsigned number
一个 位的比特串可以表示 中的所有无符号整数 (unsigned number) -
Signed number
下面我们介绍三种计算机处理符号的方式,分别有- Sign-Magnitude 符号-大小法
- 1's complement 反码法
- 2's complement 补码法
其中,现代的所有计算机都是采用 补码法 2's complement 来表达负数
-
Sign-Magnitude 原码
将比特串的 Most Significant Bit (MSB) 作为符号位 (sign bit),负数取 ,整数取
例:
在 Sign-Magnitude 表示法下,一个 位的比特串可以表示数的范围是
这一表示法虽然最便于人类理解,但是对于机器而言,实现一些运算显得很复杂 (这是符号位的缘故),以加法为例
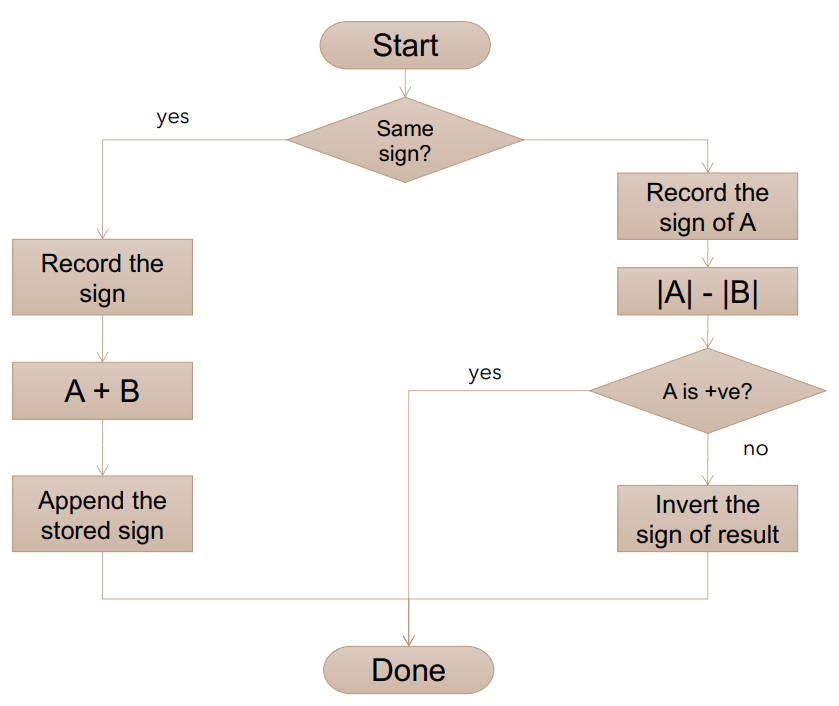
(当 符号不同时,考虑 种情况, ( 的正负号情况) ( 的相对大小情况))
并且对于 将会有两种表达: 与 -
1's complement 反码
为了将减法转化为加法,反码出现了:我们知道对于 位二进制数,减去某个数 等于加上
然而在计算 的过程中仍然要用到减法;幸运的是,对于二进制表示,对 取反码 实际上等于
反码表示法应运而生:对于正整数,其反码等于自身原码;对于负整数,其反码等于其原码除符号位以外的所有位数翻转
例:
同样,在 1's complement 表示法下,一个 位的比特串可以表示的数的范围是
反码表示法用来运算加法简单一些:

但是,这种方法对于 仍然有两种表达 与 -
2's complement 补码
在反码表示的加法中,我们仍然要通过讨论是否进位对结果进行修改 ;这是由于
那么如果我们定义补码 ,在进行加法时就无需修改结果了:因此
对于正整数,其补码等于自身原码;对于负整数,其补码等于其反码
例:对于 ,我们先写出它的原码 (4-bit 二进制表示) ,再对除了符号位外的所有位取反 获得
对于负整数补码,我们如何得到其原码:只要再进行一次求补 (取反 ) 即可
补码表示法可以直接将减法变为加法,其运算最简单 (减去一个数相当于,加上一个负数,相当于加上该负数的补码)

接下来我们对 位二进制补码表示法能表示的数的范围进行研究
在原码与反码表示中, 由于符号不同有两种表示 与 ,这明显很不自然
而在补码表示中,我们尝试求 与 :显然,
而对于 ,我们先写出其原码 ,在求反码 :此时我们发现会得到一个长度为 的串
由于二进制只有 位,MSB 将会被舍弃,于是我们又得到了 :补码完美解决了 有两种表示 , 的问题
那么, 的意义便产生了空缺
根据 (这里同样溢出了一位 )
我们规定 作为 的补码 (由于该补码原来是用来表示 的,我们指定其意义为 ,因此 在 位二进制下没有原码和反码,只有补码)
所以,在 2's complement 表示法下,一个 位的比特串可以表示的数的范围是 ,比原码或反码表示法多一个最小值 (这是由于 空出的位置) -
总结
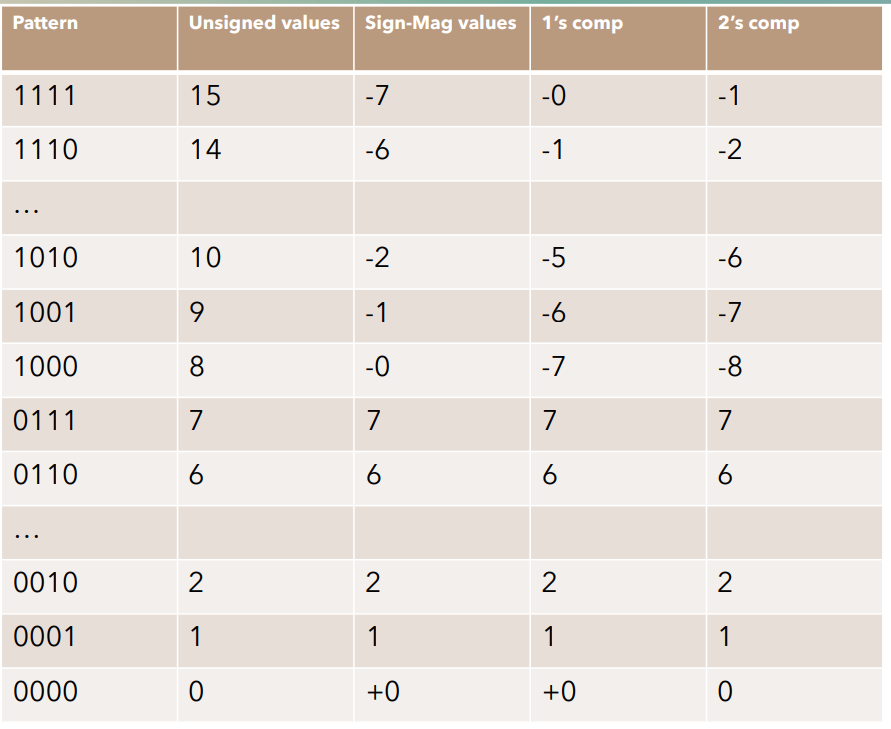
对于某一个 位二进制 pattern,若
求 unsigned values: base-position 法
是原码,求对应值:MSB 决定符号,剩余的 位进行 base-position 法
是反码,求对应值:MSB 决定符号,剩余的 位先取反,得到原码后再进行 base-position 法
是补码,求对应值:MSB 决定符号,剩余的 位先取补 (取反 ),得到原码后再进行 base-position 法;特殊的,若补码形式是 ,则对应值为
Logic Gate 逻辑门
同样也有很多干货,介绍了基础的逻辑门
-
The primitive - Logic Gate
逻辑门是对二进制数字信号的最基础控制
基础逻辑门接受 或 个信号,输出 个信号 (complex 逻辑门可接受 个信号,但输出信号只有 个)

所有的逻辑运算都能用三个特征表示:真值表 Truth Table,示意图 Schematics 与布尔表达式 Boolean Expression -
Truth Table 真值表
真值表描述对于所有输入,某个布尔函数的所有输出
All possible combinations of inputs are listed.
A truth table uniquely and completely describes a Boolean function. -
非门 NOT gate
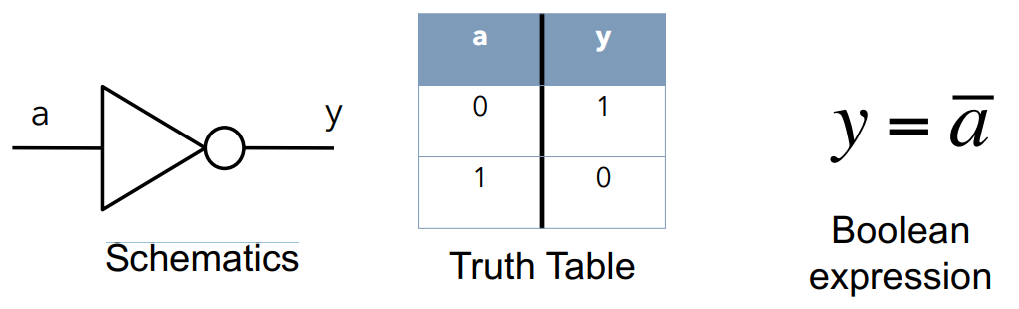
-
与门 AND gate
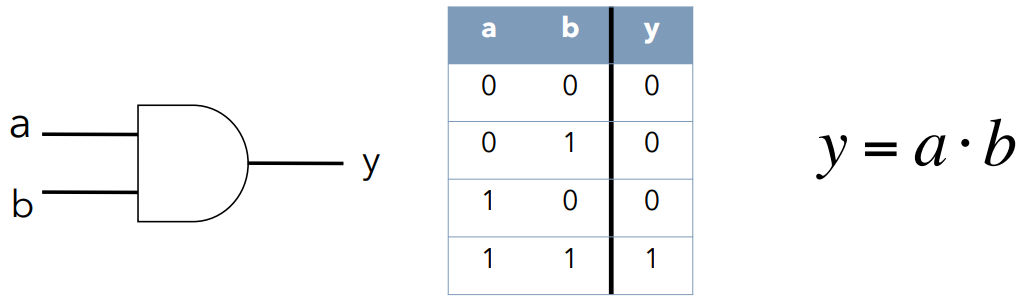
-
或门 OR gate

注意自然语言中的 "或" 与逻辑语言中的 "或" 的区别 -
Other Simple Gate
注意,所有的逻辑函数 (logic function),无论多复杂,都能被 非门,与门,或门 三个基本逻辑门进行表示- 异或门 XOR gate
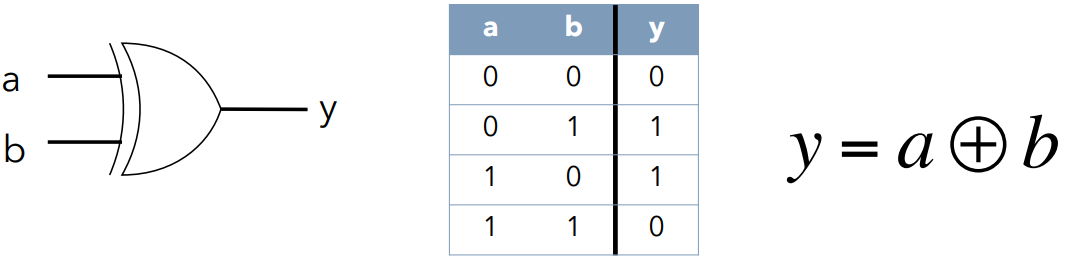
- 与非门,或非门 NAND,NOR
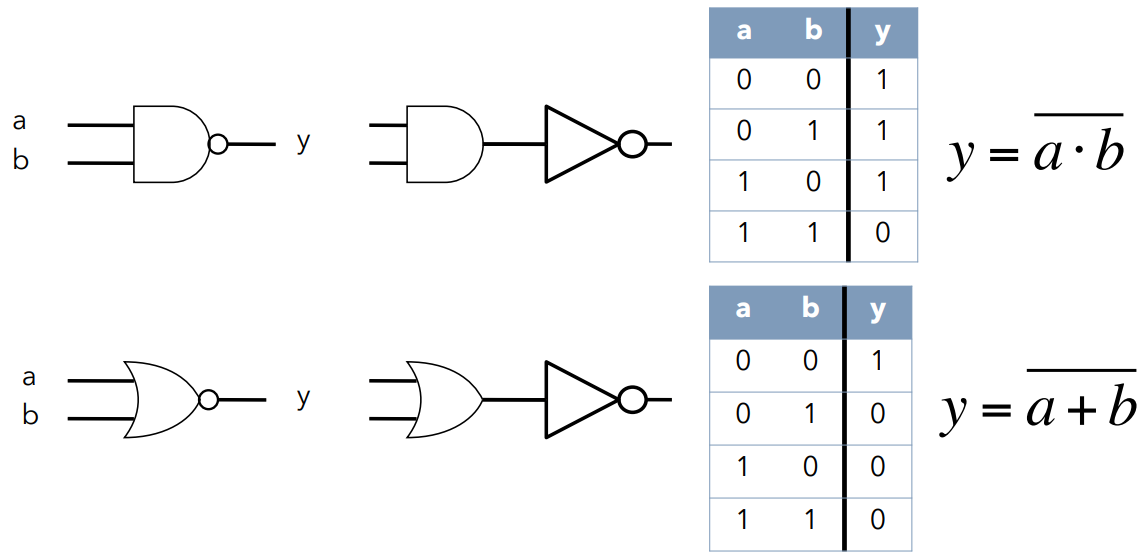
与门与非门结合,或门与非门结合
很好理解,与非门,或非门的真值表与与门,或门恰好相反;注意示意图中的泡泡 bubble 是非门的特征
- 异或门 XOR gate
-
Combinational Functions
复杂的函数能由简单的函数复合而成
我们定义一个函数是 可复合的 combinational 当且仅当它符合以下的条件- 所有组成它的函数是 combinational 的
- There is no loop in the combination
所谓 loop 循环,就是指某个输出的信号同时又作为输入产生它自身;下面的这个函数有 loop

- 任何一个输入信号只参与产生一个输出信号 (只能多对一,不能一对多)
下面的这个函数, 与 同时参与了两个信号的产生,因此不是 combinational 的

-
Hierarchy
直接当成程序里的函数就行了,很好理解:一个函数的输出可以作为另一个函数的输入
函数之间的依赖关系形成了一个 hierarchy
 、
、


-
Precedence 优先级
布尔运算中存在以下的优先级 非-与-或 (与对应乘法 ,或对应加法 )

非 NOT 的表示是上划线:例如 表示非 ;且,上划线隐式的携带一个括号,例如 实际上代表的是 即,先计算 或 再对整体取非





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异