MATH1851 Trigonometric Formula Notes

大学里老师都默认我们学过 正割 \(\sec\)，余割 \(\csc\) 与余切 \(\cot\)
还有双曲函数 双曲正弦 \(\sinh\) 双曲余弦 \(\cosh\)
再加上高中的一些公式都有点遗忘，开个贴做个笔记

常规的 \(\sin x, \cos x, \tan x\) 以及之间的关系就不说了
可以发现 \(\tan x\) 与 \(\sec x\) 一组，\(\cot x\) 与 \(\csc x\) 一组

• 正弦 \(\tan x\) (tangent):
  \(\frac{d}{dx}\tan x=\sec^2 x\)
  \(\int \tan xdx=\int \frac{\sin x}{\cos x}dx=-\frac{d\cos x}{\cos x}-\ln |\cos x|+C\)

• 正割 \(\sec\) (secant)：
  
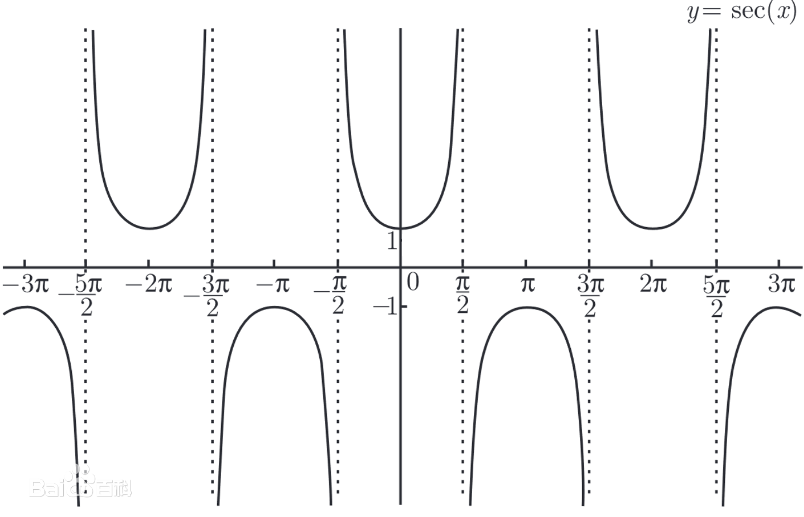
  \(\sec x = \frac{1}{\cos x}\)
  \(\frac{d}{dx}\sec x=\sec x\tan x\)
  \(\sec^2 x=\tan^2 x + 1\) (常用在三角换元解决 \(\int \sqrt{a+x^2}, x=c\tan \theta\))
  \(\int \sec x dx=\int \frac{\sec x(\sec x+\tan x)}{\sec x+\tan x}dx=\int \frac{d(\sec x+\tan x)}{\sec x+\tan x}=\ln |\sec x+\tan x|+C\)

• 余割 \(\csc\) (cosecant):
  
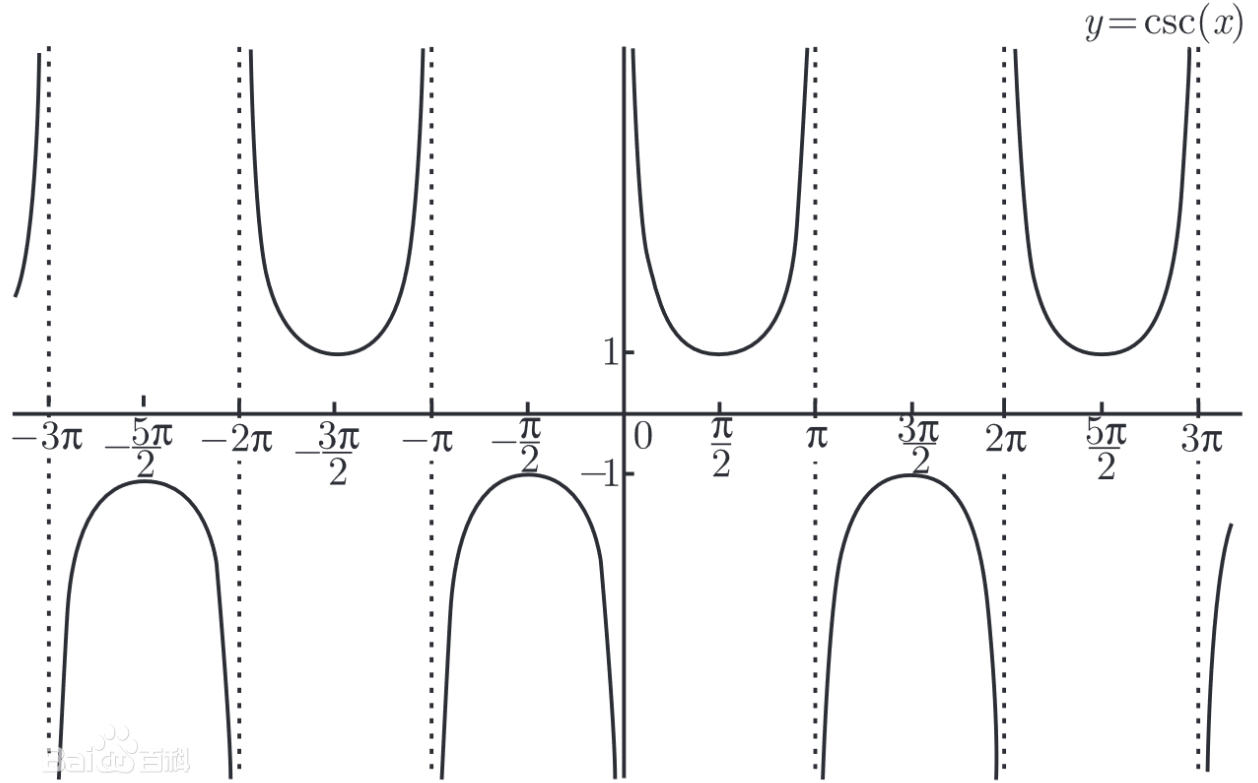
  \(\csc x=\frac{1}{\sin x}\)
  \(\frac{d}{dx} \csc x=-\csc x \cot x\)
  \(\csc^2 x=1+\cot^2 x\)

• 余切 \(\cot x\) (cotangent):
  
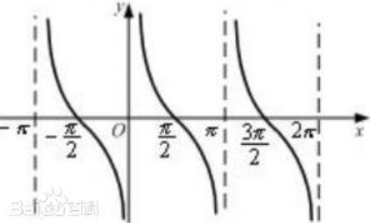
  \(\cot x=\frac{1}{\tan x}\)
  \(\frac{d}{dx} \cot x=-\csc^2 x\)

• 双曲正弦 \(\sinh\) 与 双曲余弦 \(\cosh\) 之间的关系
  \(\sinh x=\frac{e^x-e^{-x}}{2}\)
  \(\cosh x=\frac{e^x+e^{-x}}{2}\)
  \(\sinh' x=\cosh x\), \(\cosh'x=\sinh x\)
  \(\cosh^2 x-\sinh^2 x=1\)