ENGG1310 Electricity and electronics P1.3 Electromagnetic

课程内容笔记，自用，不涉及任何 assignment，exam 答案
Notes for self-use, do not include any assignments or exams

这一节主要介绍了电场理论及其应用 (Electric Field Theory and Applications)
涉及到了一部分高中知识，有点亲切

Basic Properties of Electric Charges 电荷的基本性质

• 分正负 (positive & negative)，异吸 (attract) 同斥 (repel)
• electrically neutral object 的正负电荷平衡
• 电荷守恒定律 (conservation of charge) ：在任何 isolated system 中，电荷总数 (the algebraic sum of the charges) 保持不变
• 电荷是 quantized (量子化) 的：电量的变化是分立 (discrete) 的；任何带电体的电量都是 元电荷 (basic charge) \(e\) 的整数倍

• 原子模型：带负电的 电子 (electrons) 围绕着带正电的 原子核 (nucleus) 旋转
• 原子核带正电是由于 质子 (protons) 的存在
• 自然界中几乎所有的电荷都来自于电子与质子
• 原子核中还有一种粒子 中子 (neutron)，其是中性的，不携带任何电荷 (carrying no charge)

• 在 SI 单位制 (SI unit) 中，电荷的单位是库伦 (coulomb, C)
• 元电荷/基本电荷 (basic charge) 的数值大小是 \(|Q_e|=1.60\times 10^{-19} C\)
• \(Q\) denotes for charge; \(e\) denotes for charge of a single electron/proton

Coulomb's Law 库伦定理

库伦定理是描述真空中静止点电荷之间的相互作用力的定理

注意：
r 是单位向量：若不乘上 r，公式计算的是 magnitude of \(F\)
\(\epsilon_0=8.854\times 10^{-12} \frac{C^2}{N \cdot m^2}\)：真空电容率 (the capability of a vacuum to permit electric fields)

Electric Field 电场

对于距离为 \(r\) 的点电荷 (point charge) \(Q\) 与 检验电荷 (test charge) \(q\)，它们之间的库伦力大小为

定义该点电荷 \(Q\) 的电场 \(E=\frac{F}{q}=\frac{1}{4\pi \epsilon_0} \frac{Q}{r^2}\)
电场只与点电荷 \(Q\) 与距离 \(r\) 相关，与检验电荷 \(q\) 无关

Field Lines 电场线

电场线是 虚构的，用于描述 电场强度 (Field Intensity) \(E\)

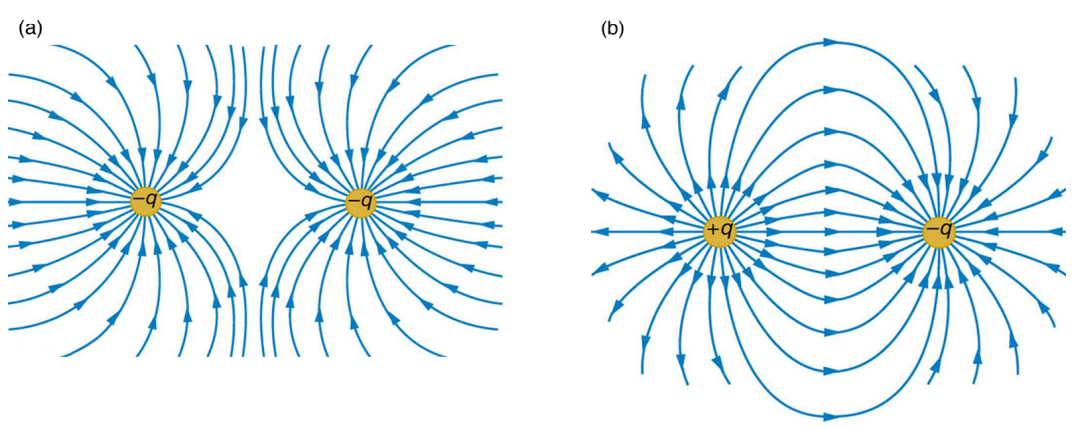
电场线上某点的电场方向：切线 (tangential to the field lines) 且指向箭头方向
电场强度：有多种表现方式：一般来说，电场线越密集 (dense) 的地方电场强度越大

Electric Flux 电通量

考虑一个球面 sphere

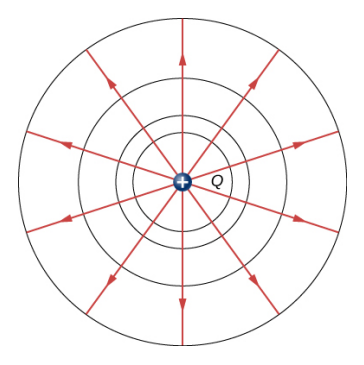
球心处的点电荷 \(+Q\) 总能引致 (by induction) 球面上产生 \(-Q\) 的电荷

我们引入电通量 (electric flux)/通量线 (flux line) 的概念
某点通量线的方向与场强 \(E\) 方向一致
且电通量与电荷量成比例 (the amount of flux is proportional to the charge)
在 SI 单位制中，\(\Psi=Q\) (即该比例的 proportion constant 为 \(1\))

与电场线相似，通量线 (flux line) 用来描述电通量的方向与大小

• 通量线由正电荷指向负电荷
• 通量线互相排斥，不会相交
• 电通量密度 (the density of electric flux) 与通量线密度成比例

根据电通量的定义不难看出，对任何闭合表面 (enclosed surface)而言
Total flux coming out \(=\) Total (+ve) charge enclosed (+ve means positive, -ve means negative)

Flux density D

电通量密度定义为

(注意：只计算垂直 perpendicular 通过该面积的电通量)
\(D\) 的方向与该点的场强 \(E\) 方向一致
\(\because D=\lim \limits_{s\to 0}\frac{\Psi}{s}\)
\(\therefore D \cdot \mathbf{ds} =d\Psi\) (ds 极小面积量: ds\(=ds \cdot\) n, n 为单位向量，方向向外垂直于该面积)
所以有高斯定律 (Gauss'Law)

(由于是对面积积分，因此这里是二重积分)

求 电通量密度 \(\mathbf{D}\)
在已知电荷分布 (charge distribution) 的情况下
找到这样一个闭合曲面 (closed surface) \(S\)，使得
在该曲面上，电通量密度 \(\mathbf{D}\) 方向要么垂直于曲面，要么是曲面的切线
这意味着在该曲面上，\(\mathbf{D} \cdot d\mathbf{s}\) 要么是 \(Dds\) 要么是 \(0\) (注意：有向与无向的区别)
在 \(\mathbf{D} \cdot d\mathbf{s}\) 不为 \(0\) 的部分上，\(D=\) constant
想要找到这样的曲面 \(S\)，需要利用电荷系统的对称性 (symmetry)

下面是几个常见的具有对称性的电荷系统

• 带电的球 (charged sphere) 或点电荷 (point charge)
• 无限长的均匀带电 line (infinite line with uniform line charge density)
• 无限大的均匀带电板 (infinite plane with uniform surface charge density)

Gauss's Law 高斯定理

• 通过点电荷 \(Q\) 在球面上的 Flux Density 推导
  
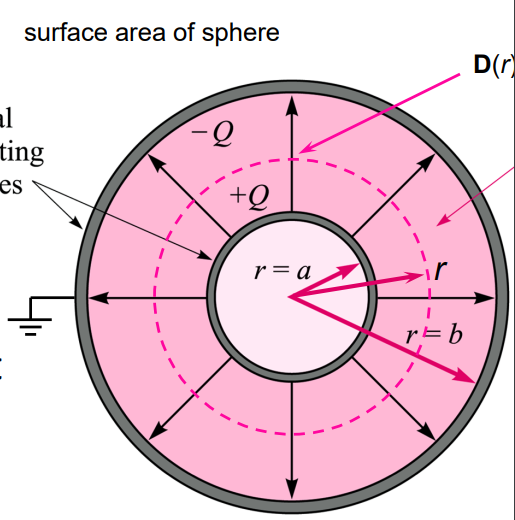
  根据对称性，点电荷在球面上的 Flux 是均匀分布的
  考虑距点电荷 \(Q\) \(r\) 处的某球面，其 Flux
  \(\Psi=Q=\iint \limits_{surface} D \cdot ds= D\cdot 4\pi r^2\) (这是因为 Flux 均匀分布)
  \(\therefore \mathbf{D}=\frac{Q}{4\pi r^2} \cdot \mathbf{a_r}\)
  与该点的电场强度进行对比
  \(\mathbf{E}=\frac{Q}{4 \pi \epsilon_{0} \cdot r^2} \cdot \mathbf{a_r}\)
  由此可得出结论 (重要！！)
  \(\mathbf{D}=\epsilon_{0} \mathbf{E}\)

• 高斯定理的积分形式 (integral form)
  
  因此
  Flux \(\Psi=\iint \epsilon \mathbf{E} \cdot d\mathbf{S}=Q\)
  这被称为高斯定理的积分形式
  此外，还有
  \(\iint \mathbf{E} \cdot d\mathbf{S}=\frac{Q}{\epsilon_0}\)
  这一形式的高斯定理 implies，在任何闭合空间 (closed space) 内，场强对面积的积分 \(=\) 该闭合空间内的净电荷量 (net charge) \(/\) 该空间的电容率 (permittivity, 即 \(\epsilon_0\))

• 高斯定理：Points to Note 1
  高斯定理是麦克斯韦方程 (Maxwell's equations) 之一
  麦克斯韦方程是四个电磁学基本方程之一

• 高斯定理：Points to Note 2
  高斯定理使得我们可以通过 电通量密度 \(\mathbf{D}\) 来计算 场强 \(\mathbf{E}\)
  (联想之前关于求电通量密度 \(\mathbf{D}\) 的对称系统)

Steady Magnetic Field 稳态磁场

• 任何磁体 (magnetic)，无论形状如何，都有南北两极
• Poles exert forces on each other (同极相斥，异极相吸)
• 单磁极 (single magnetic pole) 从未被分离出来：磁极总是成对出现
• 在永磁体 (permanent magnetic) 或 移动电荷 (moving electric charge) 周围存在
• 磁场是一个 vector (有向矢量)，某点磁场的方向即该点小磁针北极的指向
• 磁感线 (magnetic field line)
  

Magnetic Flux and Density

对比 电场强度 \(\mathbf{E}\) 与磁场强度 (magnetic field intensity) \(\mathbf{H}\)
我们提出几个相似的概念：磁通量 \(\phi\) (注意，是标量) 与 磁通量密度 \(\mathbf{B}\)
(与电通量 \(\Psi\), 电通量密度 \(\mathbf{D}\) 作比较)

由于磁极一定成对出现，所有由正极出发的磁感线 (magnetic flux line) 都将回到负极
因此，对任意闭合曲面 (closed surface)，其净磁通量 (net magnetic flux) 都为 \(0\)
(联想闭合曲面内的净电通量 net electric flux 为 \(Q\) : 这是因为正电荷可与负电荷分离，并不一定成对出现)
\(\phi=\int \limits_{S} \mathbf{B} \cdot d \mathbf{S}=0\)
这也是高斯定理应用在磁场上的表现形式

Maxwell's equation on static electric fields / steady magnetic fields

Electromagnetic Waves (EM) 电磁波

当电流变化时，相关的电场与磁场同样产生变化，并以波的形式在空气中传播
我们以这样的形式来 visualize EM：
一个交流发电机 (AC generator) 置于一条长且直的电路中央
交流发电机的运作会使电路中的电荷分布 (charge distribution) 产生变化，从而使电路周围电场强度 \(\mathbf{E}\) 发生变化
变化的电场以光速向外传播 (The changing field propogates outwards)

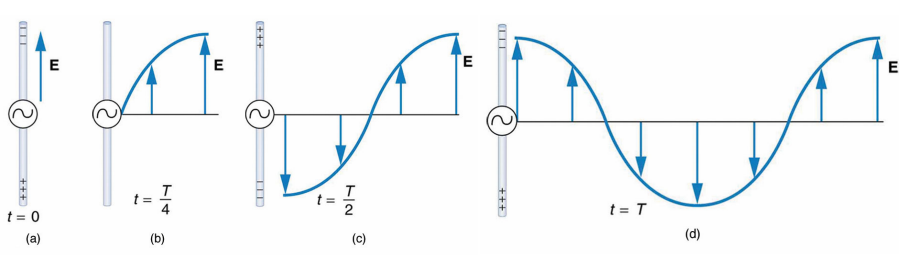
同样，周围的磁场强度 \(\mathbf{B}\) 同样会发生变化，且以光速向外传播

电场与磁场上是相互垂直 (perpendicular)的，且两者都与传播方向垂直，这样的波叫做横波 (traverse wave)

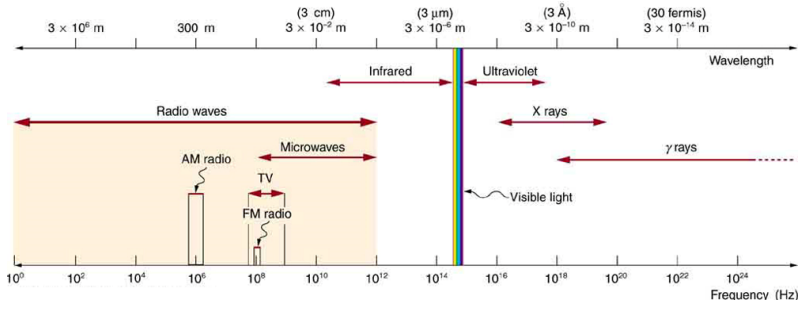
The Electromagnetic Spectrum 电磁波谱

电磁波谱根据电磁波的不同频率与波长进行分类