COMP3357 Cryptography (P1): Private-key Encryption, MAC & Hash Functions
课程内容笔记,自用,不涉及任何 assignment,exam 答案
Notes for self use, not included any assignments or exams
Course Overview
课程目标:了解现代加密学的基本原理,概念以及模型,基础的量子加密
-
Basic Principles:confidentiality (私密性),integrity (完整性), authentication (源认证)
-
Cryptographic Primitives:symmetric key encryption (对称加密),public key encryption (公钥加密),message authentication code (MAC, 消息认证码),hash functions (哈希函数),digital signatures (数字签名)
-
Basics of Quantum Cryptography:quantum key distribution, random number distribution
对称密钥加密
私钥加密 (private-key cryptography),又称 对称密钥加密 (symmetric-key cryptography), 单钥加密 (single-key cryptography), 共享密钥加密 (shared-key cryptography)
-
要求 The Task:两个诚实的用户 (honest users,与 恶意用户 malicious users 相对) Alice 与 Bob 想 communicate privately over an insecure communication chanel (例如:Internet 或 WLAN,不安全信道意味着敌手 adversary 能够窃听频道中传输的所有信息)
-
威胁 The Threat:恶意敌手 Eve 拥有频道访问权限,她能够窃听频道中传输的所有信息
-
加密目标 The Goal:Eve 无法理解 (interpret & understand) Alice 与 Bob 交流的信息
私钥 (对称密钥) 加密提供的解决办法:
- Alice 与 Bob 在某个 Secure channel (Eve 无法进行窃听) 上设立一个随机密钥
- Alice 使用该密钥 将明文 (plaintext) 加密成 密文 (ciphertext)
- Alice 将密文 通过之前的不安全信道传输给 Bob (在此过程中,Eve 只能获得于她而言无意义的密文信息)
- Bob 使用密钥 对密文解密得到明文
私钥加密除了可用于 在不安全信道上交流 (Communicate over an Insecure Channel) 之外,还可用于 数据的安全储存 (Secure Storage of Data)
此时将 Alice 与 Bob 视作不同时间段上的同一诚实用户,数据储存的设备视作不安全信道即可
私钥加密的正式定义:

私钥加密的正确性 (correctness):即
由此可以看出加密函数可能是一个随机函数 (即,对于确定的明文 与密钥 ,多次通过加密函数 加密后的密文有可能是不同的),而解密函数是一个确定函数

初探加密方法的安全性定义:关于柯克霍夫原则
- 柯克霍夫原则 Kerckhoff's principle
即使密码系统的任何细节已为人悉知,只要密钥未泄漏,它也应是安全的
- 科克霍夫原则是决定了算法公开、算法通用 (standardised encryption schemes)、加速密码算法互通的鼻祖原则
该原则也使得对密钥的储存和传输 (storage & transmission) 变得尤为重要
移位加密 (凯撒加密) 与 充足密钥空间原则
古老的对英语英语文本的加密方法,对明文中的每个字母移动 位进行加密
易证其正确性 (correctness)
由于 密钥空间 (key space) 太小,使用暴力 (brute-force) 枚举所有可能的 密钥 即可破解 ()
这就引出了加密方法的 充足密钥空间原则 (Sufficient Key Space Principle):也就是说,一个安全的加密方法应该有足够大的密钥空间以抵御暴力穷举密钥的破解法
Cryptanalysis 密码分析
- Classical attack (经典密码分析):Brute-Force & mathematical analysis
- Implementation attack (实施攻击):通过攻击特定的设施获取密钥,通常使用逆向工程 (reverse engineering)
- Social Engineering (社会工程学)
单字母替换加密 Mono-Alphabetic Substitutional Cipher
- 单字母替换加密中的密钥 是由随机的 字母排列 (arbitrary permutation of the alphabet) 所定义的
在单字母替换加密中,明文中的每一个字母在加密后都会被另一个固定的字母替代,替代的规则由密钥 代表的随机字母排列决定,而不是通过移位产生的
因此,密钥空间大小为 ,密钥长度为 。足够大的密钥空间使得暴力穷举密钥的方法对单字母替换加密无效 (infeasible) - 密钥空间大小-密钥长度与暴力穷举攻击所需时间的关系图

- 单字母替换加密的破解:频率攻击 (Frequency Attack)
如果取得了足够多的密文,通过统计每个字母出现的频率,我们就可以猜出密码中的一个字母对应于明码中哪个字母 (需要对语言中字母出现频率的先验知识)
类似的,利用语言的性质与模式 (properties and patterns of language) 进行破译也属于频率攻击
威胁模型 Threat Models
-
Ciphertext-only attack 唯密文攻击
敌手观察到若干条密文并尝试获得关于其明文的信息 -
Known-plaintext attack 已知明文攻击
敌手以某种方式得到了若干条使用同一密钥进行加密的 明文-密文对 (plaintext-ciphertext m/c pairs)。在此基础上,敌手尝试获得其他用同一密钥进行加密的密文的明文信息
已知明文攻击实例:某个机密文件若干年后公开,之前观察过密文的敌手即可获得明文-密文对。移位加密和替换加密都能够很轻易的用已知明文攻击进行破解 -
Chosen-plaintext attack (CPA) 选择明文攻击
敌手可以选择若干明文 ,并且以某种方式得到对应的明文-密文对
选择明文攻击实例:敌手给 Alice 发送了一封邮件,Alice 使用私人密钥 对该邮件进行了加密。敌手以某种方式取得了该封加密后的邮件 -
Chosen-ciphertext attack (CCA) 选择密文攻击
敌手可以选择若干密文 ,并且以某种方式得到解密后的明文
选择密文攻击实例:Alice 的电脑能对密文进行解密,敌手在 Alice 外出吃午饭的时候获得了电脑的使用权限
CCA 与 CPA 看起来相似,但实际上有能抵御 CPA 而不能抵御 CCA 的加密系统 (例 El Gamal 加密系统)
REVIEW: Basic Probablilty Theory
随机变量,概率分布,条件概率,全概率公式,贝叶斯定理
-
Probability distributions of the Key and Message

-
Probability distribution of Ciphertext
随机变量 和 是独立的: 由加密算法决定, 则与 Alice 选择发送的信息有关
我们认为 由密钥空间中随机独立的选取密钥

-
单钥加密公式 Private-key Encryption Formulae
在已知密文为 时,明文为 的概率:
(贝叶斯公式)
其中, (信息与密钥的概率分布)
(全概率公式,计算出任意特定密文的概率)
Perfect Secrecy 完美加密
-
威胁模型 Threat Model
敌手 Adversary 知道密钥函数 ,加密函数 ,解密函数 以及明文的概率分布 (特别注意,敌手是知道明文的概率分布的,这里可能与先入为主的窃听&解密印象不同)
敌手被动窃听通讯并且得到了一条 (只有一条,single) 密文
敌手并不知道 Alice 与 Bob 之间的密钥 -
完美加密:定义1

即, 的 先验概率 (apriori probability) 等于在观察某条密文后, 的 后验概率 (aposteriori probability)
也就是,密文不会向敌手泄露任何额外的关于明文的信息 (additional information about plaintext) -
等价定义2
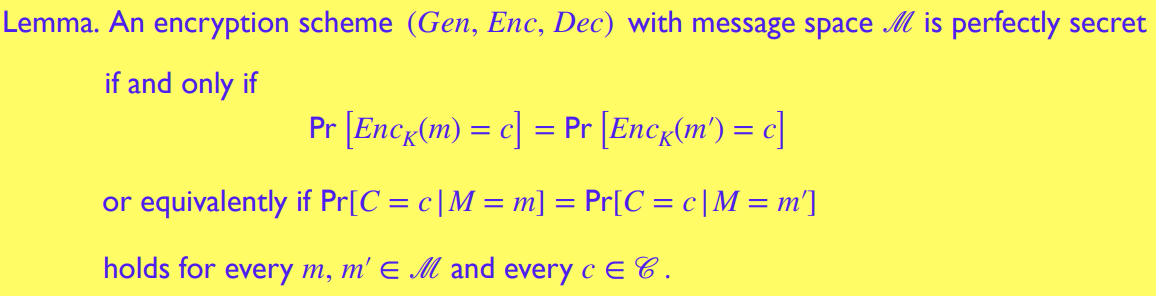
证明见 pdf:很好证,带上已知条件计算 即可发现等于 从而得证 -
等价定义3:Perfect indistinguishability 完美不可分辨性
完美不可分辨性的定义借助了一个实验:在此实验中,一个被动的敌手获得了单条密文,并尝试推测该条密文对应的明文

- 敌手选择两条明文
- 密钥函数 生成密钥 ,对应的加密函数 根据该密钥对随机对敌手选择的两条明文中的一条 进行加密,敌手获得该加密后的密文
- 敌手推测密文 对应的是原明文中的第 条
- 若敌手推测正确,则该实验的结果为 ,反之为
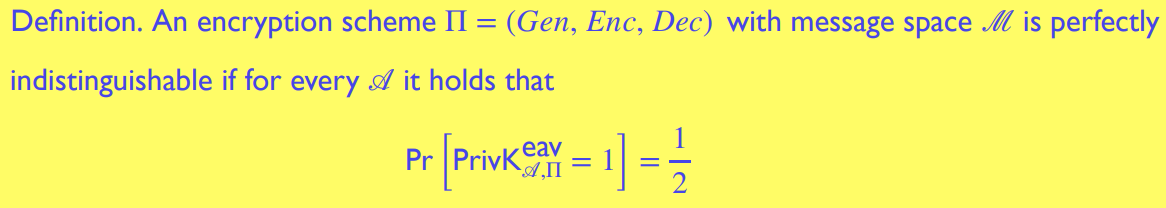
结果是 的原因:敌手随机猜测正确的概率也是
若敌手做到正确的概率超过 则该加密方案不是完美不可分辨 (即完美加密) 的
One-Time Pad Encryption Scheme 一次性密码本加密
-
Definition

- 在一次性密码本加密中,明文空间 ,密文空间 ,密钥空间 的大小是相同的 ()
(一般来说,在任何加密方案中密文空间的大小都要大于明文空间的大小 ,否则一个密文会对应多个明文,无法被解密) - 一次性密码本的加密函数是一个 确定函数 (deterministic Algorithm),即,确定的明文 与密钥 产生的密文 是唯一的 (即 )
- 在一次性密码本加密中,明文空间 ,密文空间 ,密钥空间 的大小是相同的 ()
-
正确性
一次性密码本加密是正确的:
-
一次性密码本加密是完美加密
对于确定的明文空间概率分布 ,随机确定明文 与密文
明文,密文,密钥的长度为
-
思考
这个公式我们很熟悉:
那为何 需要使用贝叶斯公式计算,而不能采用相同的逻辑?
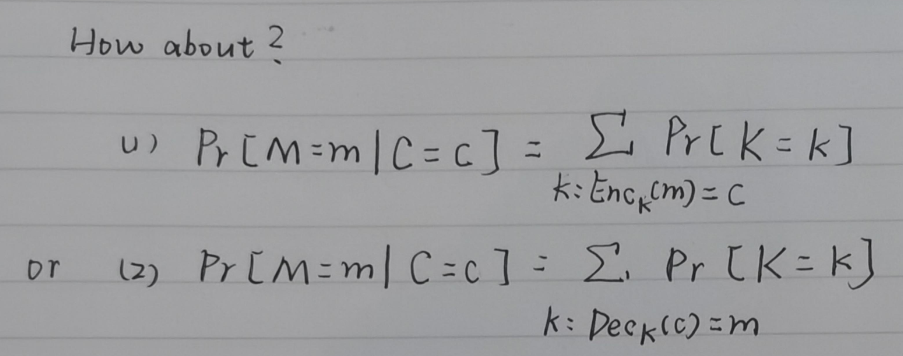
上图的 (1)(2) 两公式是等价的,同样也是错误的:举一个简单的例子
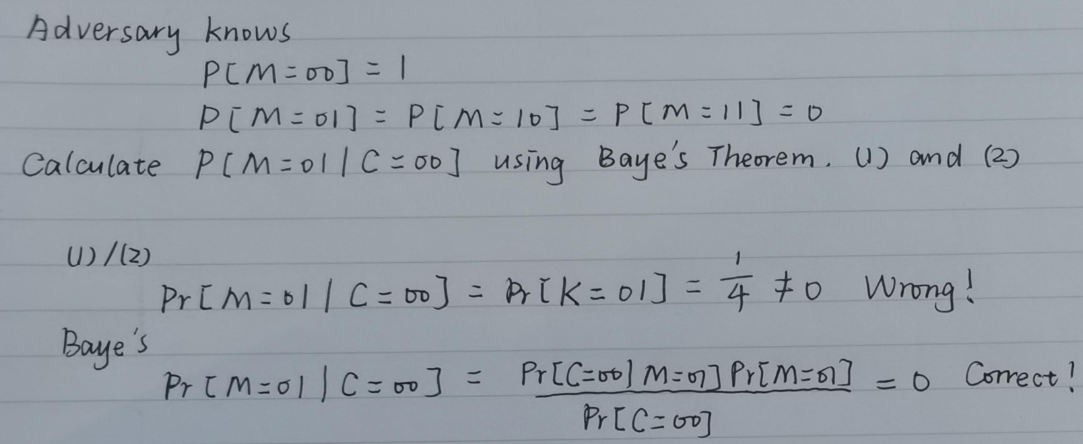
通过 (1)(2) 两公式得到的结果显然与敌手的先验知识不符
出现这样的结果,原因在于某个密文 可以有多对明文-密钥对 产生
明文空间 与密钥空间 的概率分布决定了密文空间 的分布,反之错误 (上文提到的两公式便是由 与 尝试反推 的分布) -
思考
一次性密码本加密可以完全抵挡暴力穷举的 BruteForce 攻击————即使敌手算力与时间无限,只要未获得密钥,也无法攻破一次性密码本加密

当密钥为全 串时,密文与原文一致:某人为了防止这种情况的发生,修改了密钥生成函数 ,使其不会生成全 的密钥。这种做法对吗?理论上来说,是错误的:这样做将会破坏一次性密码本的完美加密性,使得敌手可以通过密文得到关于明文的信息
-
思考 :一次性密码本的安全性在于一次性
One-Time Pad is secure only if the key is used exactly once.
若同一个密钥 加密了两组明文 ,,那么窃取到密文 , 的敌手可以得到关于明文的信息:

-
思考 :一次性密码本加密不提供消息认证 message authentication
若敌手得到了部分的明文,其可结合密文得到密钥片段
利用该密钥片段,敌手可篡改其他使用该密钥的明文片段
这进一步说明了一次性密码本加密中的密钥只能使用一次
一次性密码本加密的最优性 (Optimality) 与密码学中的香农定理
-
Optimality of the One-Time Pad
一次性密码本虽然具有完美加密性,但是其最大的短板在于密钥的长度必须大于等于明文的长度
那么存不存在这样一种加密算法,其具有完美加密性,但对密钥的长度没有限制?
很可惜,没有:可以证明,具有完美加密性的算法,其密钥空间的大小 必定 其明文空间的大小

证明如下:

-
密码学中的香农定理 Shannon's Theorem

证明见 pdf,多看几遍
计算安全 Computational Security - Relaxation of Perfect Secrecy
完美加密有固有的短板 (inherent drawbacks,即要求密钥空间大于等于明文空间),且实际生活中我们并不需要如此高强度的加密
从这个信息论上的概念出发,我们放宽限制 (relaxation),使得我们能在克服完美加密的诸多不便的同时,保证信息安全
这个概念就是计算安全 Computational Security
相比于完美加密,计算安全放宽了两个限制
- 敌手算力有限 (bounded computational power),攻击时间有限
- 加密能在极小 (tiny) 的概率下被攻破
计算安全的定义分为具体定义 (Concrete Version) 与渐进定义 (Asymptotic Version)
具体定义太过局限,因此我们主要介绍渐进定义
计算安全的渐进定义 Computational Security : Asymptotic Version
-
安全参数 Security Parameter

对每一种加密策略,我们引入安全参数
一般对应密钥的长度
根据复杂度理论 (complexity theory),我们可以用安全参数 表示加密方 (honest parties) 加密的实现时间,敌手的攻击时间 () 以及敌手攻破加密方案的概率 -
“高效”敌手:采用概率多项式时间算法攻击 Efficient (Probabilistic Polynomial Time, PPT) Adversary
引用自 这里,真的解释的很清楚
关于 Probabilistic (Randomized):意味着敌手拥有真随机数源,可获得足够长的均匀 比特串
关于 Polynomial Time:意味着算法复杂度是多项式级别的
关于高效 Efficient:在计算理论中多项式复杂度拥有特殊地位,其普遍被认为是高效的。扩展 Church-Turing 命题佐证了这一点 (见引用) -
可忽略成功概率 Negligible Success Probability
可忽略成功概率是用可忽略函数 Negligible function表示的:即在渐进意义上,比任意多项式函数的倒数小的函数
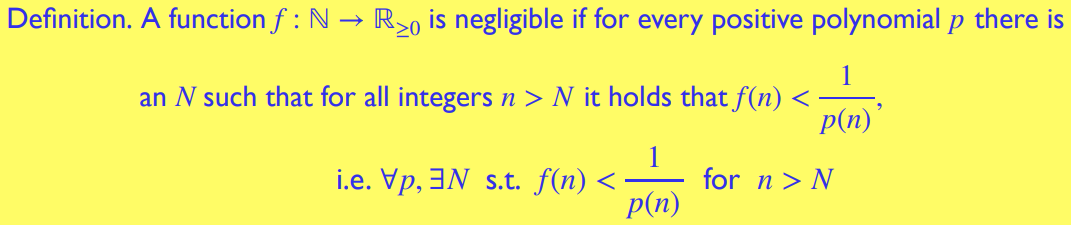
另外两种简洁一点的定义:


进行判断时用第三种很方便- 可忽略函数的闭包 (closure) 性质

- 可忽略函数的闭包 (closure) 性质
-
计算安全的渐进定义
有了上面这些概念,我们可以引出计算安全的渐进定义

当安全参数 时 ( 可视为是一个安全参数最低限制),任意的概率多项式时间算法 (relaxtion 1) 都不能以高于可忽略函数的概率 (relaxation 2) 破解该加密策略,我们说该加密策略是计算安全 (computational secure) 的 -
利用计算安全重定义 redefine单钥加密与敌手不可分辨实验
重定义的部分较好理解,回去看 pdf 即可 (注意重定义后 , , 函数的时间复杂度)
有一个点:

在完美加密中,敌手无法或者关于明文的任何信息,所以随意猜测正确的概率是
在计算安全中,由于放宽了限制,敌手尝试用 BF 来对密钥进行随机枚举从而破解加密。由于敌手的算力有限 (relaxation 1),BF 只能做到多项式级别复杂度的枚举,因此其随机枚举到正确密钥的概率是 ( 是某个多项式函数)。
因此最后敌手胜利的概率是
伪随机 Pseudorandomness
-
Intro
我们人类其实不知道如何用算法来产生真正的随机数。随机恐怕是个哲学概念,人类用概率论,随机变量来描述随机,但是真正的随机性的定义,包括概率的定义,都是高度值得怀疑的
伪随机数 (Pseudorandom numbers) 是计算安全的加密策略 (computationally secure encryption scheme) 中的重要组成部分
与真随机数不同,伪随机数是根据一系列的算法生成的:只要其通过了一系列的统计检验 (efficient statistical test),我们就视其为随机数

-
Statistical Test 统计检验

注意,所有的统计检验都是多项式级别复杂度的算法 (efficient)
下面是一些统计检验算法的例子:
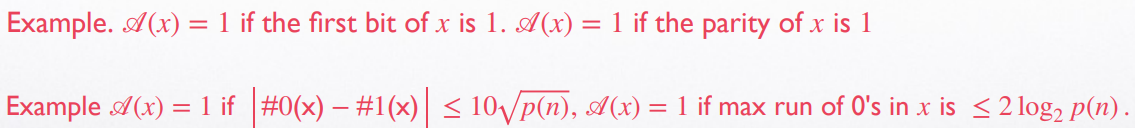
经过统计检验的伪随机数列将会被视作真随机数进行使用,由此可以看出Pseudorandomness is a relaxation of true randomness
-
Definition

先看前置定义:伪随机的概念是定义在一系列分布 上的

随着 增加,distinguishing probability 将会趋近于
Pseudorandom number generators (PRGs/PRNGs)
-
Intro
-
Prerequisite Definition
有许多前置定义:
:将短随机种子 (种子是由 uniform distribution 产生的真随机短串) 扩大为长的伪随机数串的函数

( 函数) 定义了一系列分布 :若这一系列 满足伪随机定义,则称 为伪随机数发生器 (Pseudorandom gernerator)

注意: 函数一定是 deterministic 的 :保证种子作为唯一的随机性来源

-
Formal Definition

注意,虽然种子 是真随机,均匀选取的,但是 并不是

由于 是 deterministic 的,所以一个种子对应一个扩大的伪随机数串:所有 输出的 长度的伪随机数串占所有该长度数串的 -
Example: PRG or not?

No.
Check parity of , if parity is , outputs
if , then
if , then (任意 串的 位是其前 位的校验码的概率为 )
is non-negligible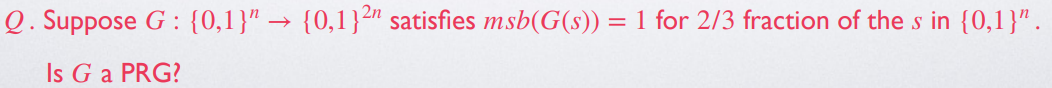
No.
Check msg of , if msg is , outputs
if , then (题目条件)
if , then (msb 为 的串占所有串的 )
is non-nengligible
(a)
(b) , A distinguisher for can output "not random/0" when the last bit is not
(c)
(d)
(e) , A distinguisher for can output "not random/0" when the first bits does not equal to the last bits -
Notes on PRG (1)
如果我们定义算法 为:判断当前数串是否是由某个 seed 经过函数 产生,若是,输出
那么最终的 distinguishing probability 为
可以发现,由于 远大于 ,这个概率其实是 non-negligible 的
那么岂不是说明任何函数 都不是 secure PRG 了?
这个误区是因为没有考虑到 的复杂度:实际上,对于所有的 secure PRG,算法 的复杂度是不能做到多项式级别的 -
Notes on PRG (2)
虽然有关于 secure PRG 的具体定义,但是遵照这一定义仍然很难判断某个算法 究竟是不是 secure PRG.


secure PRG 的存在可建立在另一个假设 :单向函数存在 (there exists one-way function),但同样这一假设也是未经验证的

Linear Congruential Generator (LCG, 线性同余发生器)
一种 PRG:注意,它是 not cryptographically secure 的


Blum Blum Shub Generator
一种 PRbG (pseudorandom bit generator):它是 cryptographically secure 的 (至少目前来说)


注: 与 是 relatively prime 的,意味着
其安全性在于 difficulty of factoring: 类似于单向函数 (one-way function) 的概念,两个大质数 与 的相乘 是很简单的,然而将 因式分解 (factoring) 比较困难
相关:二次剩余问题 Quadratic Residuosity Problem
Pseudo One-Time Pad / Stream Cipher
-
Intro
One-Time Pad 虽然具有完美加密性,但最致命的缺陷就是其密钥 的长度必须与明文 的长度相等
我们可以利用 PRG 来弥补这一缺陷
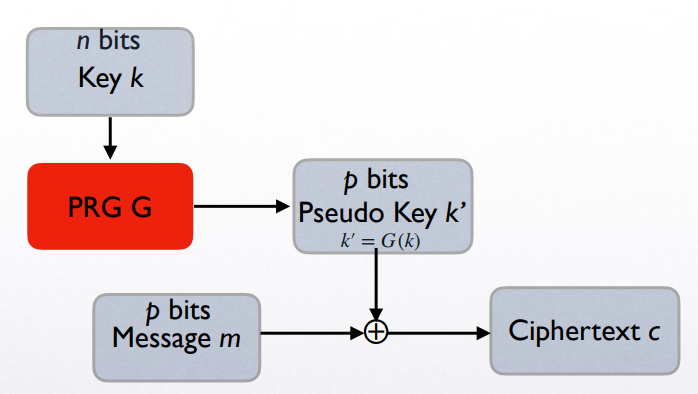
选取随机种子作为密钥 ,利用 PRG 产生与明文 长度相等的伪随机序列 :这样,the parties 在安全信道上只需传输长度较小的密钥 -
Definition
Pseudo One-Time Pad 可以建立在任意的 PRG 上;其仍是一种单钥加密方案 (private-key encryption)

与 OPT 类似,Pseudo OPT 的正确性 (Correctness) 易证 -
(重要) Pseudo One-Time Pad : Computational Security

我们将用 proofs of Reduction (归约法) 进行证明
关于归约法十分精彩的解释:我们假设存在PPT的敌手 (adversary) 可以以不可忽略 (non-negligible) 的优势 (advantage) 攻破此密码方案,那么通过归约 (reduction) ,就可以同样以不可忽略的优势破解该困难问题。这与我们对该困难问题已知的困难性 (hardness) 相互矛盾 (contradiction) ,所以不可能存在这样的敌手去攻破我们的密码方案,因此他是安全的。

Assumption:G 是 (secure) PRG
Protocal to be proved: Pseudo One-Time Pad/Stream Cipher 是 EAV-secure -
Proof : Pseudo One-Time Pad is EAV-secure
这里的逻辑有点难绕,具体的证明见 pdf:这里我主要梳理一下自己的逻辑已知: 是一个 secure PRG:即,任何敌手都无法以高于 的概率分辨 与
对于 true OTP,即使用真随机密钥的 OTP 方案,敌手是无法攻破的 (OTP 的 perfect secrecy)
对于 pseudo OTP,若敌手能在 EAV-secure 实验中取得胜利 (即,敌手以不可忽略的优势攻破了 pseudo OTP),意味着敌手能够以某种方式分辨密文 是由伪随机密钥 加密还是由真随机密钥 加密的求证:若敌手攻破了 pseudo OTP,则其亦可以攻破 secure PRG
(逻辑:这里的求证逻辑是这样的,已知 secure PRG 是一个难以攻破的 困难问题;若我们能求证敌手攻破了 pseudo OTP 代表攻破了 secure PRG,则其逆否命题 secure PRG 安全代表 pseudo OTP 安全也成立;结合 secure PRG 是一个难以攻破的困难问题,可推出 pseudo OTP 难以攻破,从而得证)
证明:

通过归约思想,我们构造一个 distinguisher ,其以尝试攻击 pseudo OTP 的敌手 作为子程序 (subroutine):这样成功将 pseudo OTP 的 EAV-security 与 secure PRG 联系起来。我们假设 以不可忽略的优势成功攻破了 pseudo OTP 的 EAV-security;此时, 可将 作为预言机 (oracle):若 在 EAV-secure 实验中成功分辨出正确的明文 ,代表其发现了密钥是伪随机的 (因为根据完美加密性,若密钥是真随机的, 无法分辨出正确的明文,即其成功的概率是 ), 从而输出 ;这就意味着若 pseudo OTP 被攻破,secure PRG 同样会被攻破。而这个结论与 secure PRG 问题的困难性矛盾,我们由此推出 pseudo OTP 是 EAV-secure 的 -
Pseudo One-Time Pad:Points to note

利用 PRG,我们得到了 EAV-secure 的改良 OTP 算法,从而解决了 OTP 算法密钥必须与明文等长的难题

但是,OTP 算法密钥只能使用一次的缺点并没有得到解决
接下来我们将会寻找密钥较短且可重复使用的安全加密方案 (CPA-security) -
Two-Time Pad is insecure

无论是同一密钥加密多次,还是密钥之间存在联系,都会大大降低安全性 -
OTP and pseudo OTP is malleable
当密钥只使用一次时,OTP 与 pseudo OTP 均提供私密性 (confidentiality),但不提供完整性 (message integrity)

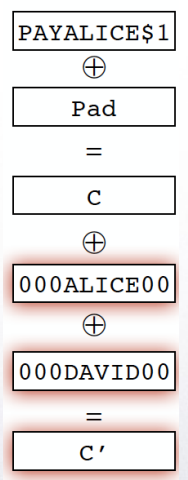
Multiple-message secrecy and CPA-secure
-
Mutiple-message secrecy
在不安全的信道上使用同一密钥 与加密策略加密 多条 消息
若这样的加密策略是安全的,则称其有 multiple-message secrecy
显然,OTP 是不具有 mutiple-message secrecy 的 -
Chosen-Plaintext Attacks 选择明文攻击
之前我们接触了唯密文攻击 ciphertext-only attacks:唯密文攻击是假定密码分析者拥有密码算法及明文统计特性,并截获一个或多个用同一密钥加密的密文,通过对这些密文进行分析求出明文或密钥
而选择明文攻击 CPA 给予敌手更多的优势:攻击者拥有加密机的访问权限 (oracle access),可构造任意明文所对应的密文
具体来说,敌手自主选择若干条明文 ,并通过加密机获取对应的密文 。此时敌手被挑战者给予用 同一密钥 加密 的密文 ,并尝试获取其明文 -
CPA security

一个加密方案是 CPA secure 的意味着其能抵抗 CPA 攻击
且,一个 CPA secure 的加密方案一定也是 multiple-message secure 的 -
CPA Indistinguishability Experiment : CPA 不可分辨实验

CPA 不可分辨实验与 EAV 不可分辨实验的区别在于:CPA 不可分辨实验中的敌手时刻拥有加密机的访问权限 (oracle access to )

-
CPA security : definition
定义在 CPA 不可分辨实验上的 CPA security

-
A CPA security encryption scheme must be RANDOMIZED

注意,由于敌手拥有对加密机的 oracle access,他可以对任意指定明文进行加密,包括 CPA 不可分辨实验中的

这意味着 CPA 安全的加密方案必须是一个随机算法 (randomized algorithm):也就是说,相同的明文 与密钥 可对应多个不同的密文
否则,敌手仅需要通过比对挑战者给出的密文 与通过 Oracle access 得到的结果 就能攻破 CPA security

-
CPA security 的衍生定义:CPA secure for multiple encryption
-
CPA security means CPA security for mutiple encryption

任意单钥加密方案是 CPA-secure 的,则其在多次加密中也是 CPA-secure 的
注意这与 EVA-secure 的不同:单次加密 EVA-secure 的某个单钥加密方案不一定是多次加密 EVA-secure 的,例如 OTP 与 stream cipher
Pseudorandom Functions and Permutations
-
Intro
之前我们提到,一个 CPA-secure 的单钥加密方案算法必须是 randomized 的:为了构建 CPA-secure 的单钥加密方案,我们引入伪随机函数的定义
Pseudorandom Functions (PRFs) 本质上是对于某 input,output 随机的函数 -
Random Functions 随机函数

对于输入有 种,输出有 种的函数集 ,其大小 ,因此上例中的

随机函数即在以上的函数集 中随机均匀抽取的某个函数
解释一下第二个 equivalence:一个随机函数对应一个长度为 的串。想象一下我们随机生成一个该长度的串,将其分为 份,每一份的长度为 ;这样,对于 种输入 都有其对应的长度为 的 -
Keyed Functions

在我们的研究中,keyed function 中的 key ,输入 与输出 长度一致,即
并且,函数 是一个 PPT 的算法

-
Pseudorandom Functions : definition 伪随机函数

几个注意:- 符号 与 代表 有对其的 Oracle access,即 可以对 Oracle 进行 PPT 次询问并得到对应的答案
- distinguisher 的任务是,判断预言机 是伪随机函数 还是真随机函数
- 为什么 获得的是 与 的 Oracle access 而不是整个算法:(注意,在之前的不可分辨实验中,敌手是知道具体的加密策略的) 这是因为,一个真随机函数 random function 要用 位表示,而 PPT 的 distinguisher is limited to polynomial time,无法得到该指数级的输入
- 重要!函数 与 都是 deterministic 的:虽然 是真随机函数 random function,但这一"随机"体现在它是在 中随机选取的;一旦选定,它就固定下来。同样,伪随机函数 一旦选定了 ,其对 的分布也随之固定。distinguisher 可以是 randomized 的
- 是不知道密钥 的!

-
Diagram intro:
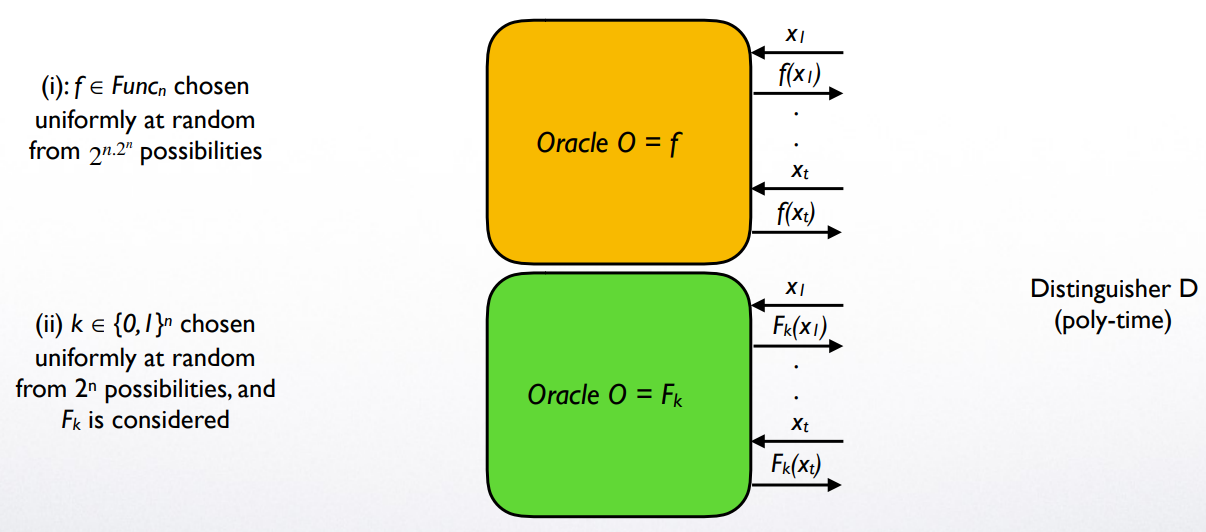
F is pseudorandom if the 2 diagrams above are indistinguishable for any efficient
例子:

当 oracle 是真随机函数 输出 概率是 的原因: 有 种取值 -
Random Permutations 真随机排列
定义真随机排列
中包含了所有长度为 的串到长度为 的串的排列,因此 -
Keyed Permutaions

我们只研究 length-preserving 的 Keyed Permutation,即
并且,Keyed Permutation 也必须是 efficient 的:即 与 对任意 polynomial 的 ,其算法都在 polynomial time 内
若一个 efficient, keyed permutation 是伪随机的,意味着任何 PPT 敌手都无法区分 与真随机排列 -
Strong pseudorandom permutations

对于一个强伪随机排列,PPT 敌手 将会被给予 的 oracle access
Block Ciphers (区块加密) 是应用强伪随机排列的一个实例 -
PRG from pseudorandom functions 用伪随机函数构造 PRG

将 视为 可能更好理解 (这里强调的主要是它们的两两不同)
由于 ,构建 PRG 的 expansion factor
可通过归约证明,安全的伪随机函数构造的 PRG 也一定是安全的,
且通过 Extended Church-Turing Thesis,PPT 的伪随机函数构造的 PRG 也一定是 PPT 的

-
pseudorandom function from PRG

利用 PRG,我们可以构造一个 block length 较小的 PRF
记得之前在介绍 Random Function 的时候提到过,random function 实际上就相当于生成一个长度为 的串
这里我们利用类似的思想,由于明文 长度定义为 ,因此明文空间大小为
我们利用 PRG 生成长度为 的串,分成 份,每份的长度都为 :选择第 份作为结果
这样就得到了一个 polynomial-time 的,用 PRG 来构造的 pseudorandom function
CPA-secure Encryption from Pseudorandom Functions
-
Definition

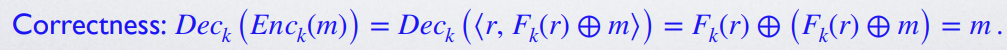
注意,密钥是 , 是加密 Enc 时产生的一个辅助随机量!也就是,对于每次加密,都会随机产生一个
且 是密文 中的一部分:这意味着敌手可以获取
与信息 等长 -
CPA-secure Encryption V.S. Pseudorandom OTP (stream ciphers)
我们会发现 CPA-secure Encryption 与 Pseudorandom OTP 很相似
它们采取的方案都是将某个 pseudorandom pad 与明文按位异或产生密文 (对于 CPA-secure Encryption,该 pad 是 ,对于 pseudorandom OTP,该 pad 是 )甚至可能我们会产生这样的疑问:既然 CPA-secure Enc 中的 能随机产生,我们为什么不直接将其与明文进行异或,或是采取 pOTP 中利用 PRG 扩展 的方案,而是大费周章的设计一个伪随机函数 和辅助随机量 来产生 pseudorandom pad 呢?
这就涉及到 CPA-secure 与 EAV-secure 的区别
我们可以发现,CPA-secure Enc 中的密钥 可以重复使用加密多条信息,而保证密钥复用安全的关键就在于随机的 :它确保了 是 randomized 的,对于相同的 与 , 的结果是随机的
而对于 pOTP,其加密方案是 deterministic 的,这也导致其不能多次使用同一密钥,不具有 CPA-secure -
Security of the CPA-secure encryption scheme : Designing proof of reduction

对这一套应该有点熟悉了:基于安全的 定义的 ,在证明 的安全性时使用归约证明
构建 PPT 敌手 尝试攻击 CPA-secure Enc;构建 distinguisher 尝试区分 random function 与 pseudorandom function,并将敌手 作为子程序 (subroutine)
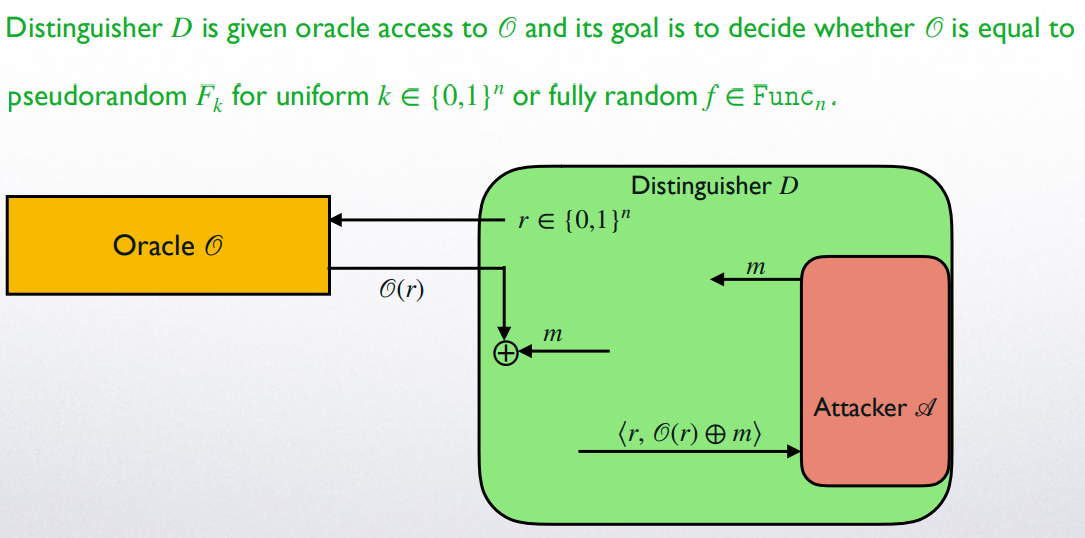
归约开始, 为敌手 模拟 (emulate) 实验环境- 执行 ,敌手输出两条文本
- 随机选择
- 模拟 加密方案:随机产生 ,询问 (query) 预言机得到 (这里不用提供 ! 见伪随机函数 的定义),在对 进行加密形成挑战文本 (challenge ciphertext) 并将其发回给敌手
- 敌手 在产生 之前,可能会对 模拟的预言机进行若干次询问 (这是 CPA 敌手 的能力):对于每次询问 , 随机产生 并向上级预言机询问得到 ,后以 作为对 的回答
- 敌手输出 :若 , 输出 (not random),反之输出
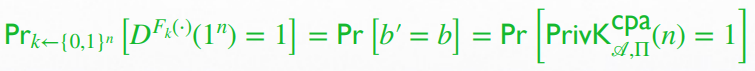
通过归约,我们将这两个概率关联在了一起:若某敌手以不可忽略的优势攻破了 EAV-secure,那么 pseudorandom function 也同样会被攻破
详细的概率证明见 PDF Lect 7,具体思路如下- 通过归约机,证明当 是真随机函数 时,敌手 赢得 CPA-secure 实验胜利的概率 (在此 EAV-secure 实验中使用的函数是真随机函数 ) 输出
not random的概率,记为 - 通过归约机,证明当 是伪随机函数 时,敌手 赢得 CPA-secure 实验胜利的概率 (在此 EAV-secure 实验中使用的函数是伪随机函数 ) 输出
not random的概率,记为 - 计算出当 是真随机函数 时敌手 胜利的概率 (分为 repeat 与未 repeat 两种情况)
- 根据伪随机函数的定义我们有
- 整理 (3)(4) 得 ,又 也是可忽略得,于是 CPA-secure 得证
Block Cipher Modes of Operations 区块加密法工作模式
-
Encrypting arbitrary length message

利用 CPA-secure 对多条信息加密保密的特点,我们可以将长信息分为若干条短信息进行加密
但是可以发现,由于密文是 形式,密文的长度是信息长度的两倍,也就是说,ciphertext expansion factor 是

-
Block Cipher Modes of Operations :区块加密法工作模式
应用 Block Cipher Modes of Operations,我们可以对长消息进行加密的同时将密文长度限制在一定范围内

注意:谈到 Block Cipher 时,运用较多的是 (伪)随机排列 (Pseudo)Random Permutations
我们将会介绍三种区块加密模式:CBC,ECB 与 CTR
Cipher Block Chaining mode (CBC)
-
CBC: Cipher Block Chaining mode

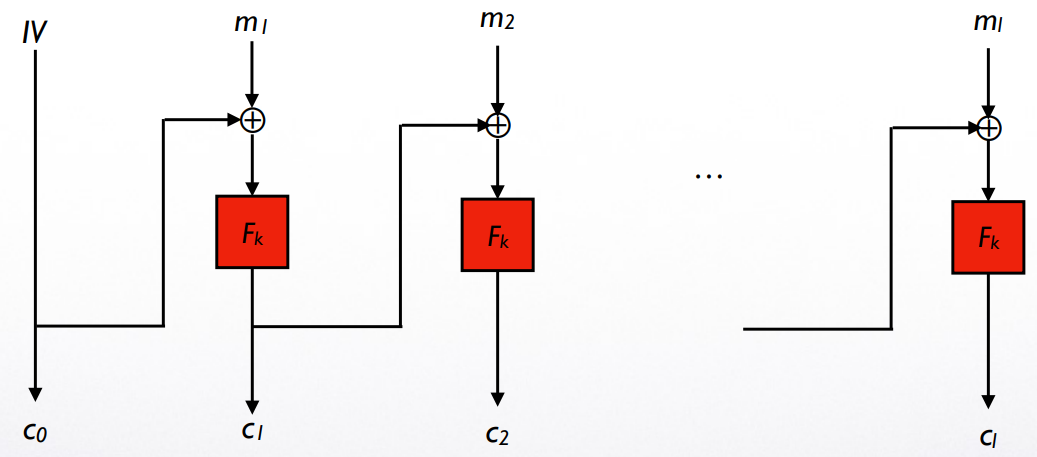
CBC 的加密过程不是 parallelizable 的,因此效率较低 (insufficient):想加密第 个 block 必须先完成前 个 block 的加密
但 CBC 的解密过程是 parallelizable 的:解密第 个 block 只需要第 个 block 的信息即可CBC 的加密同样是 randomized 的,这是由于 的选取是随机的 (与 CPA-secure encrypt scheme 中的 作用相同)
CBC 加密的 ciphertext expansion 仅有 1 block:长度增加了 (即 )
-
altering CBC scheme Version 1

这个问题中的算法甚至都不是 EAV-secure 的:
我们列出用该方法加密时的加密序列可以发现,当构造 的第一个 block 与第二个 block 相等时
其对应的密文的第二个 block 的结果即为 ,也就是第零个 block 的结果 (这是由于 是 deterministic 的)我们再构造一个不满足该特点的信息
这样,当检查 challenge text 时,若我们发现 的第零个 block 与第二个 block 相等,输出 ,否则输出 ,这样就破解了该算法的 EAV-secure
至于敌手更强的 CPA-secure 就更加不用说了 -
altering CBC scheme Version 2

这里的||代表或

(答案来自本课 TA : Zhang, C. )
思路是通过全 串得到一个与 无关的量 -
altering CBC scheme Version 3
若采用 CBC 加密时,每次加密时并不随机选取 ,而是将该次加密的 设为上次加密时的 加一 (即 )
这样的策略是 CPA-secure 的吗
已知上一次对信息 加密的结果 :
若我们构造一个 使得 ,即
即可在 加密后观察到
所以该策略甚至不是 EAV-secure 的 (思路很像版本 ,构造特殊的 ,该 可以使其对应的 展现出某些可预测的结果) -
Chained CBA mode & TLS-CBC-IV attack

Chained CBA mode 不是 CPA-secure 的:具体可看下面这个例子

Eletronic Code Book (EBA) mode
ECB mode 没有任何的 ciphertext expansion

简单粗暴,对每一个分组直接应用伪随机排列
然而,由于 ECB 的加密算法是 deterministic 的,所以其不可能是 CPA-secure 的
甚至,由于其用相同的密钥分组加密了多条信息,其连 EAV-secure 都无法做到

Counter mode (CTR)
-
Definition

最重要的概念是 counter (计数器),其初始值 随机指定,对每一组密码 ,并生成对应的 pseudorandom pad
同样,为了 decryption,该 ctr 的初始值需要作为密文进行传递
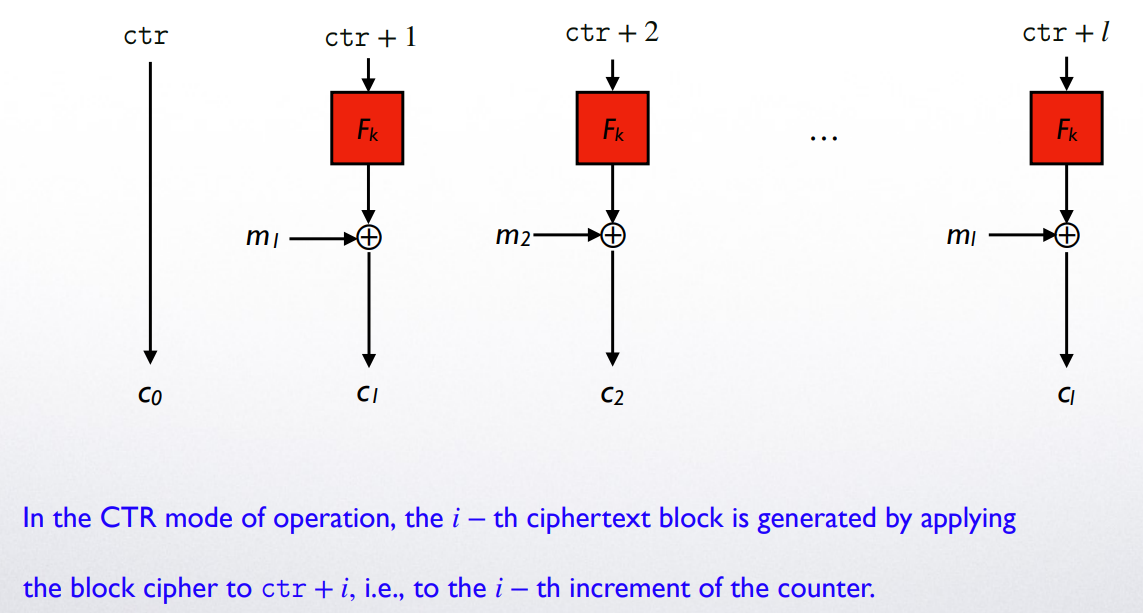
-
Points to Note
CTR 的 并不要求是伪随机排列,只规定是伪随机函数 (pseudorandom function)
注意:当我们使用伪随机函数 进行加密时,潜意识是想利用其的逆 进行解密
CTR 的解密 并不需要知道 (其利用的是求出 block 对应的 pseudorandom pad 并利用异或抵消)
注意,CBC 的解密 是需要知道 的,因此在其加密定义中 指的是伪随机排列对 pseudorandom pad 的处理甚至可以在收到信息 (message) 之前进行:这是因为其完全独立于明文的内容
CBC 则不行,因为其每一个 block 所对应的加密处理都依赖于上一个 block 密文的内容CTR 更为高效 (efficient):其加密与解密均是 parallelizable 的
如果 CTR 中的 counter 并非完全随机 (fully random) 的,那么其安全性将比 CBC 更低:若 ctr 被破解,则整个密文都有被解密的风险;而 CBC 中的 被破解并不会对整个密文造成这么大的威胁
-
CTR mode : security

Block cipher : Practical Issue
研究完这 CBC, EBA 与 CTR 三种加密方式后,我们来考虑 Block cipher 在使用时可能出现的实际问题
-
block length 太短
当 block length 过于短时,即使强伪随机函数也不能保证 block cipher 的安全性 -
初始化随机量的随机性
若 (即 CTR 中的 ) 随机性较弱,则 CBC 比 CTR 更为安全 -
Non-Adversarial Transmission Error 非敌手传输性错误
传输时可能出现错误,例如:丢包 (dropped packets),change bits 等等,这样接收方得到的密文解密后将会与明文有出入
不同的加密方式发生传输错误后的表现不同
存在 error correction,re-transmission 等机制进行纠正 -
关于 CBC 与 CTR 中的 single-bit error
CBC:
经过加密后
若 中有一位发生了 single-bit error 成为 ,考虑 Dec 还原出来的明文 会受到什么影响
(因此, 与正确的明文 完全无关)
(由于 ,所以 与正确的明文 相比只有一位是翻转的)
因此,CBC 中的某个 block 只会影响到密文中的第 与 第 个 blockCTR:
<m_0, m_1, m_2, ...> 经过加密后
同上,考虑 中有一位发生了 single-bit error
( 与正确的明文 相比只有一位是翻转的)
因此,CTR 中的某个 block 只会影响到密文中的第 个 block
Active Attacker : Chosen-Ciphertext Attack (CCA)
-
Intro
在 CCA 选择密文攻击中,敌手不仅能够进行 CPA,还允许敌手选择一系列密文并且得到它们解密后的原文
一个主动的敌手 (active adversary) 能够假装发送者,向接收者发送一系列密文,并观察解密后的原文 -
Definition : CCA 不可分辨实验 (CCA Indistinguishability experiment)

注意:
敌手同时拥有 与 的 oracle access
敌手不能用 Dec 的 oracle access 来解密 challenge ciphertext -
CCA Security


很明显不是,假设我们得到的 challenge ciphertext
则
我们构造密文 并输入 Dec 得到
于是我们将 得到
得到 后,使用 即可得到明文
(第二种利用 single-bit error 的方法见下面的 malleability 相关) -
CCA Security : Multiple Encryption


即,一个 CCA-secure 的加密方案,对多重加密一定也是 CCA-secure 的 -
Malleability

加密方案的 malleability 是指,若对密文进行修改,将观察到可预测的改变
完美加密 (prefect secrecy) 并不代表 non-malleability:例如,OTP 就是一个 malleable 的加密方案
Alice 翻转密文中的某一位将会导致 Bob 接收到某一位翻转的明文
一个 non-malleable 的加密方案应该是这样的:若敌手将密文 修改成 , 要么弹出错误信息,要么生成一个与正确的明文 完全无关的新明文 -
CCA-security and Malleability

简要证明:若加密方案 是 malleable 的,则意味着敌手可以通过修改密文,经过 Dec 后观察到可预测的改变
那么,在进行 CCA 不可分辨实验时,敌手可修改 challenge ciphertext 为 ,并通过 Dec 的 oracle access 观察可预测的改变,即,通过 与真正明文 的对比从而推出真正的
由此我们可以得出,凡是 malleable 的加密方案一定不是 CCA-secure 的;
而 CCA-secure 的加密方案一定具有 non-malleability
Overview of Information Theory Concepts 信息论的基本概念
-
熵 Entropy
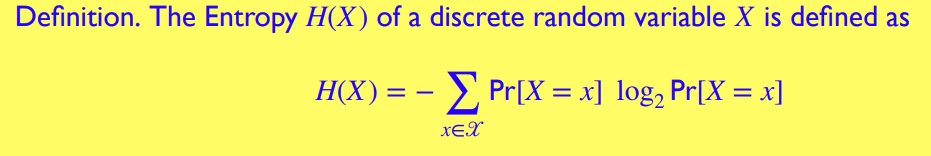
熵是 的期望,即
熵描述的是信息的不确定性 (uncertainty),也就是说,一个确定的信息,其熵为
一般而言, (例,一个取值有 种的信息,每一个取值均匀分布 其有着最高理论熵 ) -
条件熵 Conditional Entropy

条件熵是 的期望,即
条件熵描述的是,在已知 的情况下, 的不确定性
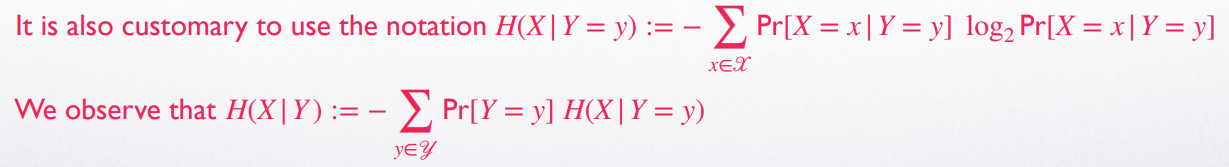
注意, 可以这样理解:得知 并不会增加 的不确定性;若 与 独立,则 -
Chain Rule and other entropy relations
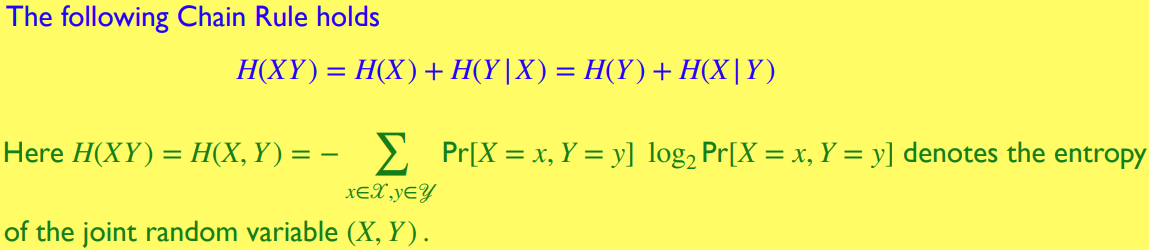
联合的不确定性: 的不确定性 加上已知 后, 的不确定性
可根据 证明, 当且仅当 独立时取等号 -
相对熵 Relative Entropy
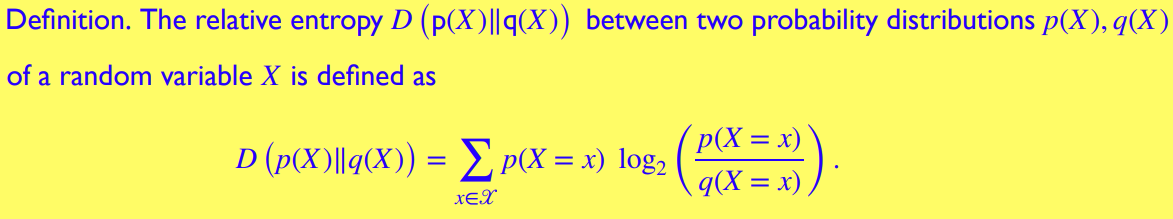
相对熵可视作两个 关于 的概率分布的距离 (distance)
或者说是 "the inefficiency of assuming distribution q(X) when the correct distribution is p(X)"
一般来说, -
互信息 Mutual Information
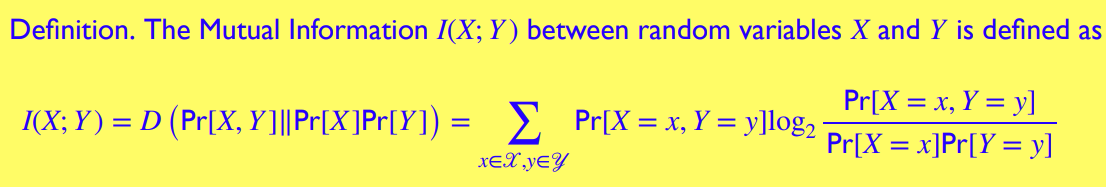
互信息用来描述两个变量之间相互依赖的程度,具体来说是 随机变量 由于已知随机变量 而减少的“信息量/不确定性”
换句话来说,也是已知 的情况下,我们得到的关于 的信息 ( 减少的信息量被我们得到/我们增加了对 的确定性)
互信息也可以用来描述将 视为独立变量的代价 (price) (实际上 , 并不相互独立)

互信息的性质可以很容易由上面的几个描述推理出来
( 原来的不确定性 减去已知 后 的不确定性 得到 减少的不确定性)
注意 , -
密钥熵与信息熵 Key Entropies & Message Entropies
接下来,我们将尝试用信息论里的术语来重定义完美安全
先介绍密钥熵与信息熵的概念:
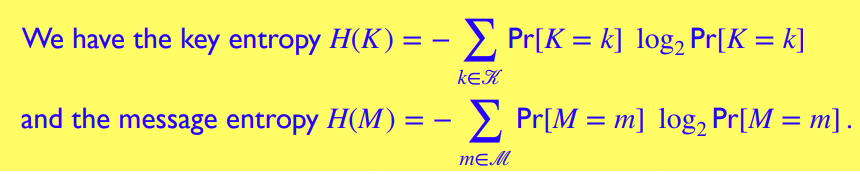
密钥熵与信息熵是对于敌手 而言的:密钥与信息的熵 (不确定性 uncertainty) 根据敌手的先验知识 (a priori) 进行计算
当敌手观察到 ciphertext 后,密钥与信息熵可被描述为
由于观察到 只可能使密钥熵与信息熵减少 (less uncertain),所以有 -
Perfect Secrecy in Information-Theoretic terms

即, 与 相互独立:敌手观察到 并不会使 的不确定性减少,即

对任何完美安全的加密方案,密钥的不确定性一定 信息的不确定性:这也是为什么香农提出任何完美安全加密方案中,密钥的长度一定 信息的长度
证明:
首先,根据 Chain’s Rule, (given ; 联合熵 given ; 的熵 given ; 的熵)
由于 是一个确定的算法 (即,已知 , 一定能得到 ),所以有
所以
又有 (联合变量 的不确定性不会比 的不确定性小)
所以
又 (conditioning doesn't increase entropy), (安美加密的定义)
所以有
Message Authentication Code 消息认证码
-
Integrity V.S. Secrecy
Message Integrity 是指:保证消息是由发送方 (intended party) 发送而来,而未在传输过程中被更改 (来源有两种:传输错误或敌手的恶意更改)
消息认证码 (Message Authentication Code, MAC) 是一个保证 message integrity 与 authentication 的 Cryptographic primitive
一个加密方案可以是 secret without integrity 的:例如完美加密的 OTP 是 malleable 的
一个加密方案可以是 integrate without secrecy 的:例如在 MAC 保护下直接在公共频道上发送未经加密的消息
这是由于:Encryption does not provide Integrity -
MAC:Definition


-
MAC 安全性证明:MAC-forge 实验
 、
、
注意:
敌手不知道
敌手拥有 MAC 的 oracle access
敌手不能通过 产生最后的 (联想到 CCA 中,敌手不能通过 还原 challenge ciphertext )

与之前的 EAV-security, CPA-security, CCA-security 实验对比,这里的概率是 而不是
这是因为:之前的实验都是不可分辨 (indistinguishability) 实验,而这一实验要求敌手尝试自主生成 valid 的 对,因此没有可以通过随机猜测获取的概率
(Lec 9 p.15 有相关问题):(unbounded computational power adversary; ; No, ) -
Replay Attacks : 重放攻击
以上我们介绍的 MAC 是无法抵御重放攻击的,因为它是 stateless 的
高级的 MAC maintain state:通过 sequence number (synchronized counter) 与 时间戳 (time-stamp) 来抵御重放攻击 -
Construct a Fixed-Length MAC
A Fixed-Length MAC 指的是,消息 与密钥 等长的 MAC
我们用伪随机函数 来构建一个固定长度的 MAC

-
Security of the Fixed-Length MAC Construction

证明的模式与证明 CPA encryption 安全性的模式一模一样
首先构造归约:
尝试分辨伪随机函数 与真随机函数 ,并利用敌手 作为其子程序 (subroutine)
敌手 进行 Message Authentication 实验
当 利用 Oracle access 权限向 query 时, 就对 进行询问,并将结果发回给
若最后 的输出是 valid 的:即 则 输出 否则输出由于归约成立,以下两个式子均成立:
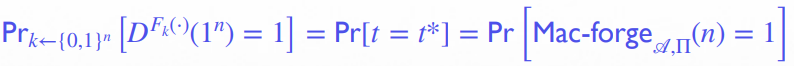
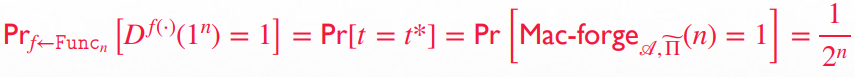
第一个式子是 是伪随机函数 的情况
第二个式子是 是真随机函数 的情况:由于 真随机, 不能通过研究 预测到 ,因此其能做出的最好决策只有输出一个随机的 :而 的概率是
两式相减之后整理得到

需要注意的是,Not All PRFs are secure MACs
对于 PRF:
若 数量级则 MAC 不安全 (因为 此时变为 non-negligible) -
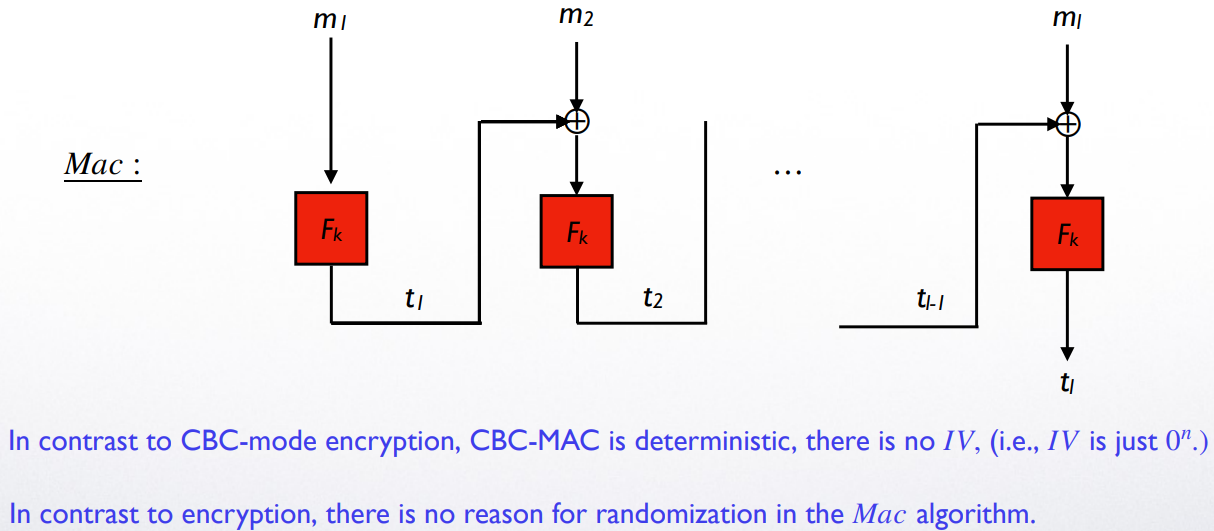
MAC for longer messages:CBC-MAC construction
之前我们介绍了定长 MAC:这种 MAC 要求信息长度 与密钥 一致
而 CBC(CipherBlock Chaining)-MAC construction 允许对更长的信息进行 MAC

与 CBC 加密进行对比:- CBC-MAC 是 deterministic 的,其 ,而 CBC 加密是随机化的,其 要随机选取才能保证 CBC 的安全性
- CBC-MAC 只输出一个 block 作为 MAC tag

(这个问题我自己想出来了!这样修改后的 CBC-MAC 无法通过 Message Authentication Experiment)
根本原因是:
CBC-MAC 中的敌手 需要产出 ,意味着其可以自主选择 即 的生成
而 CBC 中的 是由 Enc 随机生成的,敌手无法进行操作,其只能操作
具体 attack:
query with 得到
若
构造 与 MAC
可证明 是 valid 的

-
Security of the Basic CBC-MAC construction

CBC-MAC 安全当且仅当 是固定的 (另一种形式上的 fix-length:虽然密钥长度不一定要与信息长度等长,但是**信息的长度是固定的 **)
注意 指的是 block 的数量, 指的是每个 block 的长度
若信息长度不固定,敌手可在 MAC security 实验中胜出
下面是当信息长度不固定时,敌手通过长度 的信息与 的信息攻破长度为 信息的 CBC-MAC 安全
queries with ,
gets corresponding
could construct a valid -length and tag
Thus CBC-CMC for messages whose length are is insecure
当信息长度固定时,Oracle 不会对敌手传入的长度非 的信息进行回应 -
CBC-MAC for arbitrary-length messages
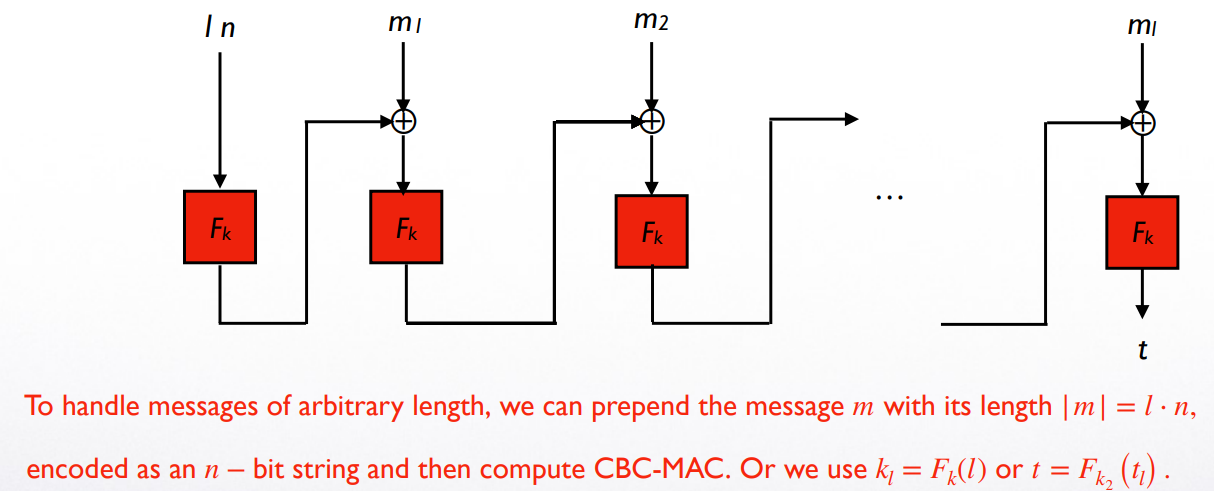
若我们需要传输非固定长度的信息且需要保证 CBC-MAC 安全,有三种改良方法- 将信息长度 以 位的 string 表示,插入到信息的首端 (作为第一个 block)再计算
- 计算 并以 作为执行 CBC-MAC 的密钥
- 计算 并使用 作为最后的 tag
可以发现这些方法都是在 Basic CBC-MAC 中添加了与 相关的随机性
Hash functions & Hash-MAC
(注意复习 exercise)
-
Hash Functions: Intro
哈希函数能够将 任意长 (arbitrary length) 的输入串 压缩 (compress) 成 长度固定的短串 (short, fix-length digest)
一个哈希函数越优秀,其避免 冲突 (collision) 的能力就越强

若任何敌手都无法在 PPT 时间内找到哈希函数 的冲突,我们说 是 collision resistant 的 -
Keyed Hash Functions

关于 的注意:- 不是所有的 都是 valid keys: 一般由算法 产生,not necessarily in a uniform manner
- 与 不同, 的 并不要求保密:也就是说,我们要求 的 collision resistant 建立在敌手已知 的情况下
-
Hash Functions: Definition

注意在 fix-length Hash functions 中, 是 的长度,而 是 的长度 -
Collision-Finding Experiment:
与各种加密方法一样,我们采用定义实验的方法来说明哈希函数的安全性,即 collsion resistance

-
Hash Functions: Security definition (collision resistant)

如上文介绍,哈希安全可以指 collision resistance (冲突抗性),这是哈希安全的一个最强的定义
除此之外,还有两个常见的弱化定义 (weaker notion),Preimage resistance (原像抗性) 与 Second-preimage resistance (次原像抗性)
下面我们将介绍这两个较弱的定义并探索这三个定义之间的关系 -
Preimage Resistance 原像抗性

即,不存在任何 PPT 敌手可以通过哈希值 找到其原像 ;在这个过程中,哈希函数与 均被敌手掌握
本质上而言,原像抗性代表着 是一个 one-way function: easy to compute, difficult to recover -
Second-preimage Resistance / Target-collision Resistance 次原像抗性

次原像抗性可以看作是冲突抗性 (collision resistance) 条件的放松:
在冲突抗性实验中,敌手掌握 与哈希函数 ,要求输出 使得
而在次原像抗性实验中,敌手掌握了 , 与一条信息 :其只需要输出另一条信息 使得 即可 -
Collision Resistance implies Second-preimage Resistance
若 有冲突抗性,则其有次原像抗性
对于这类证明,我们可以通过证明他们的逆否命题来进行 (若想要正面进行证明,使用传统的 proof by reduction + 概率,PDF 上有具体过程)

注意,具有次原像抗性的 不一定是具有冲突抗性的,下面构造了一个具有次原像抗性但不具有冲突抗性的

(这里可以计算敌手赢得 second-preimage attack 实验的概率,可以发现是 negligible 的 - Lec11 Rec. 00:40:34) -
Second-preimage Resistance implies Preimage Resistance
若 有次原像抗性,则其有原像抗性
类似的,通过逆否命题

若 subroutine 执行 preimage attack 时返回的 ,simulator 不能攻破次原像抗性
而输出 (在平均意义上),而一般来说,,所以
同样,具有原像抗性的 不一定拥有次原像抗性,见下例

-
Secure Hash
总的来说,哈希的三个安全定义遵循这样的关系
冲突抗性 Collision Resistance (最强) 次原像抗性 Second-preimage Resistance 原像抗性 Preimage Resistance
这里我想分析一下自己对于定义的强 strong 与 弱 weak 的理解
所谓强的定义,指的是对敌手的限制最少:若在这种定义下敌手都无法攻破方案的安全性,则说明该方案安全性很强
由此可以推出,若某个方案在强定义下是安全的,则其在弱定义下也是安全的
若某个方案的弱安全定义被攻破,则其强安全定义一定也会被攻破 -
Attack on Hash: Bruteforce

-
Attack on Hash: Birthday problem 生日悖论

在介绍生日攻击之前,我们先介绍生日悖论 (Birthday Problem)
首先,需要说明的是,在设计哈希算法的一般攻击 (general attack) 时,我们一般将哈希算法视作完全随机函数:因为我们设计的是一般攻击,这样的攻击是不会对不同哈希方案的特点进行分析的

生日悖论 (Birthday problem) 与 Balls into Bins 问题和这样的问题模型是一致的

经过证明(见下), 个 balls 随机 分配到 个 bins 里,当 时,存在 个 bin 中有 个 balls 的概率约为

-
Attack on Hash: Birthday attack 生日攻击

这样,我们构造了一个复杂度为 的攻击算法,比 BruteForce 要优秀很多
Birthday Attack 的两个 implications:


-
HASH-MAC: Message Authentication using Hash Functions
引入可看 PPT —— Lec11 的 idea 部分:
注意,直接使用 Hash Functions 作为 MAC tag 是不可行的,因为 Hash 的 是被敌手所掌握的,因此不能舍弃原来的 MAC 算法
使用 Hash-MAC 本质上来说是一种让 Fixed-Length MAC 认证 arbitrary length message 的一种方式

-
The security of HASH-MAC construction

若 fixed lengthed MAC 是 unforgeable 的且 Hash Functions 是 Collision Resistant 的,那么 HASH-MAC 同样是 unforgeable 的


在正式证明中,需要构造两个 proof of reduction:
1 是通过 的敌手攻破 的冲突抗性
2 是通过 的敌手攻破 的安全性 (在未发生冲突的情况下)
具体可看 PPT
Authenticated Encryption 认证加密
-
引入与一些概念总结
Integrity:即 unforgeability,敌手无法 forge 出 valid 的密文 (在 实验中) 或 对 (在 实验中)
一个 non-integrity 的消息可能在传输过程中被篡改,或是由敌手传输的假消息 (forged message)
Unforgeable MAC 能够提供 Message Authentication 与 Integrity
Confidentiality 与 Integrity 是正交的概念:它们都是信息安全的重要组分,然而拥有 Confidentiality 并不意味着 Integrity,拥有 Integrity 也并不意味着 Confidentiality
我们已经分别介绍了提供 Confidentiality 的各种 Encryption 方法与提供 Integrity 的各种 MAC 方法
接下来,我们要求将这两者结合起来:既提供 Confidentiality (保密性),又提供 Integrity (完整性),这样的加密方法被称为 Authenticated Encryption

这里的保密性指 CCA-security -
Malleability 与 Integrity
注意,non-malleability don't imply any types of integrity
我们可以参考 non-malleability 的定义

可构造一个 unforgeable 的加密方案 (这说明其提供 integrity),但它是 malleable 的 (详见 tutorial 2 slides) -
Adding MAC to a private-key encryption
注意,密文 经过了加密 与 MAC 两种算法的某种 combination 而产生

-
The Unforgeable Encryption Experiment
联想 MAC 的 Unforgeable Encryption Experiment
敌手尝试构造一个有效的 使得
而对于加密方案 ,敌手尝试构造一个有效的 ,使得 而不会出现错误

-
Authenticated Encryption : Definition
先定义添加了 MAC 后的 private-key encryption 的 unforgeable,即其提供 integrity

即,通过了 实验的加密方案是 unforgeable 的
若该加密方案还能通过 实验 (敌手获得 ),则该加密方案是一个 Authenticated Encryption -
Constructions for Authenticated Encryption
我们知道,在 Authenticated Encryption 中,获得密文 的算法是由 与 以某种方式 combine 而成的
具体来说,有以下三种 combination:- Encrypt-and-authenticate: 加密与认证分别独立进行

- Authenticate-then-encryption: 先进行认证,将 tag 与 m 合并后进行加密

- Encryption-then-authenticate: 先对 plaintext 进行加密,再认证密文

- Encrypt-and-authenticate: 加密与认证分别独立进行
-
Encrypt-and-authenticate (Eaa)
- Eaa 的组合可能甚至无法提供 EAV-security
这是因为 可能会泄露关于原文 的信息:毕竟,MAC 算法提供 integrity,却不一定提供 confidentiality
若 是 unforgeable 的 MAC,可以证明 同样也是 unforgeable 的
然而,这一 unforgeable 的 算法提供 保密性:它把原文 完全泄露了 - 若 Eaa 组合中的 MAC 算法提供了一定保密性 (例,EAV-secure),但如果其是 deterministic 的,则多次 MAC 后会泄露关于原文的信息 (原理与多次 OTP 不是 CPA-secure 的原理相同)
因此,Encrypt-and-authenticate 组合并非 Authenticated Encryption
- Eaa 的组合可能甚至无法提供 EAV-security
-
Authenticate-then-encrypt (Ate)
Ate 组合得到的加密方法可能不是 CCA-secure 的,我们通过一个例子来说明

由于是 CTR mode,易知该 是 CPA-secure 的:但其与任意 unforgeable 的 MAC 通过 Ate 形成的加密方法不是 CCA-secure 的
敌手在 实验中获得的 challenge ciphertext 为

事实上,这个加密方法也不提供 integrity (unforgeablilty)
在观察到 后,敌手能够产生一个全新的 使得 而不输出错误
这也符合 malleable 的方案一定不提供 integrity 的规律 -
Encrypt-then-authenticate (Eta): Secure!
Eta 组合先对原文进行加密,再对得到的密文 进行认证,最后输出
若 ,输出 ,否则输出错误
可以证明,任意 CPA-secure 的加密方法与 strong unforgeable 的 MAC 经过 Eta 组合后形成的加密方法是一个 Authenticated Encryption

- Strong Unforgeable MAC

Strong Unforgeable MAC 给予了敌手更少的限制:若敌手连 Strong Unforgeable MAC 都无法攻破,就更加无法攻破 Unforgeable MAC 了

(这是因为 canonical 定义下的 MAC 本身就是 deterministic 的)
证明:
Unforgeable:

若敌手要产生一个全新的,有效的 ,其必须产生一个全新的 对;
由于 MAC 是 strong unforgeable 的,因此无法以 non-negligible 的优势实现
(若 MAC 是 unforgeable 的,则可能存在敌手能以 non-negligible 的优势找到 ,其中 ,而 , 与 均是 的两个可能的 tag)
CCA-secure:

这里将 CCA-secure 归约到 CPA-secure 的方法是:由于 MAC 的存在, 无法使敌手获得任何额外的信息 - Strong Unforgeable MAC
-
Independent Keys for Encryption and Authentication
加密与认证的密钥必须是不同的:见下例

使用相同密钥进行加密与认证,即使加密是 CCA-secure 且认证是 unforgeable 且采用 Eta 形式组合的加密方法,最后甚至会将原文完全泄露 -
Attacks on Authenticated Encryption
有三种针对 Authenticated Encryption 的攻击,分别是
Replay Attacks,Reorder Attacks,Reflection Attacks (很好理解,见 Lec 12 Slides)
在信息中加入 counter 与 identity 等信息可以阻止这些攻击,这被称为 Secure Sessions using Authenticated Encryption





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异