微积分 II 笔记
5.1 定积分的概念
-
定义
定积分是积分的一种,是函数 \(f(x)\) 在区间 \([a,b]\) 上积分和的极限
若 \(f(x)\) 在 \([a, b]\) 有界,在 \([a, b]\) 上任意插入 \(n\) 个分点将区间分为 \(n\) 个小区间 \(\Delta x_1, \Delta x_2, ..., \Delta x_n\)。在每个小区间上都任取一点 \(\xi_i\)
记 \(\lambda=\max\{\Delta x_1, \Delta x_2, ..., \Delta x_n\}\)
那么 \(f(x)\) 在 \([a, b]\) 上的定积分 \(\int_{a}^{b} f(x)dx=\lim \limits_{\lambda \to 0}\sum_{i=1}^{n} f(\xi_i)\Delta x_i\) -
定积分只与被积函数与积分区域有关系,与积分变量无关:\(\int_{a}^{b}f(x)dx=\int_{a}^{b}f(t)dt\)
-
函数连续即可积;若函数有界,且有有限个间断点,那么也可积
-
定积分的几何意义
若在 \([a, b]\) 上
\(f(x)\geq 0\):函数 \(f(x)\) 的图像,直线 \(x=a, x=b\) 与 \(x\) 轴围成的面积
\(f(x)\leq 0\):\(...\) 围成的面积的相反数
\(f(x)\) 有正有负:\(f(x)\geq 0\) 的部分形成的面积减去 \(f(x)\leq 0\) 的部分形成的面积 -
用定义求定积分
求 \(\int_{0}^{1} x^2 dx\)
将 \([0, 1]\) 等分成 \(n\) 份,则 \(\Delta x=\frac{1}{n}, \xi_i=\frac{i}{n}\)
\(\int_{0}^{1}x^2 dx=\lim \limits_{n\to \infty} \sum \Delta x f(\xi_i)=\lim \limits_{n\to \infty} \sum \frac{1}{n}(\frac{i}{n})^2=\lim \limits_{n\to \infty}\frac{1}{n^3}\sum i^2=\lim \limits_{n\to \infty}\frac{n(n+1)(2n+1)}{6n^3}=\frac{1}{3}\)
5.2.1 定积分的性质
- \(\int_{a}^{a}f(x)dx=0\)
- \(\int_{a}^{b}f(x)dx=-\int_{b}^{a}f(x)dx\) (可由性质 \(1\) 推出)
- \(\int_{a}^{b}(\alpha f(x)+\beta g(x))dx=\alpha \int_{a}^{b}f(x)dx+\beta \int_{a}^{b}g(x)dx\)
- \(\int_{a}^{c}f(x)dx=\int_{a}^{b}f(x)dx+\int_{b}^{c}f(x)dx\) (类似向量)
若 \(a<b<c\),上式易证 (直接采用几何意义进行理解)
若 \(a<c<b\),该式仍然成立:\(\int_{a}^{c}f(x)dx=\int_{a}^{b}f(x)dx-\int_{c}^{b}f(x)dx=\int_{a}^{b}f(x)dx+\int_{b}^{c}f(x)dx\) (运用了性质 \(2\)) - 若 \(f(x)\geq 0\),则 \(\int_{a}^{b}f(x)dx \geq 0\)
- 若 \(f(x)\leq g(x)\),则 \(\int_{a}^{b}f(x)dx\leq \int_{a}^{b}g(x)dx\)
- \(|\int_{a}^{b}f(x)dx|\leq \int_{a}^{b}|f(x)|dx\)
- 设 \(M, m\) 是 \(f(x)\) 在 \([a, b]\) 上的最大值与最小值,则有 \(m(b-a)\leq \int_{a}^{b}f(x)dx \leq M(b-a)\)
即 \(\int_{a}^{b} mdx \leq \int_{a}^{b}f(x)dx \leq \int_{a}^{b}Mdx\) - 定积分中值定理:\(f(x)\) 连续,\(\exist \xi \in [a, b]\),$\int_{a}^{b}f(x)dx=f(\xi)(b-a)
这一定理由 \(8\) 即可推出:由于 \(m\leq \frac{\int_{a}^{b}f(x)dx}{b-a}\leq M\),所以一定 \(\exist \xi\in [a, b], f(\xi)\in [m, M]\) 使得 \(f(\xi)=\frac{\int_{a}^{b}f(x)dx}{b-a}\)
5.2.2 微积分基本定理
-
积分上限函数
\(p(x)=\int_{a}^{x} f(t)dt, x\in [a, b]\)
积分上限函数的导数 \(p'(x)=f(x)\)- 上限是 \(x\),直接将 \(x\) 代入被积函数:\(p(x)=\int_{a}^{x} f(t)dt, p'(x)=f(x)\)
- 下限是 \(x\),将 \(x\) 代入被积函数后加负号:\(p(x)=\int_{x}^{a} f(t)d(t)=-\int_{a}^{x} f(t)dt, p'(x)=-f(x)\)
- 上限是 \(g(x)\):\(p(x)=\int_{a}^{g(x)}f(t)dt\),令 \(u=g(x)\),则 \(p(x)=y=\int_{a}^{u}f(t)dt\),采用复合函数求导链式法则,\(p'(x)=\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}=f(u)u'=f(g(x))g'(x)\)
- 上限是 \(g(x)\),下限是 \(h(x)\):\(p(x)=\int_{h(x)}^{g(x)}f(t)dt=\int_{h(x)}^{a}f(t)dt+\int_{a}^{g(x)}f(t)dt=-\int_{a}^{h(x)}f(t)dt+\int_{a}^{g(x)}f(t)dt=-f(h(x))h'(x)+f(g(x))g'(x)\)
-
积分上限函数的例题

-
牛顿-莱布尼茨公式 (微积分基本公式)
揭示了定积分与被积函数的原函数或者不定积分之间的联系
\(\int_{a}^{b} f(x)dx=F(x)|_{a}^{b}=F(b)-F(a)\)
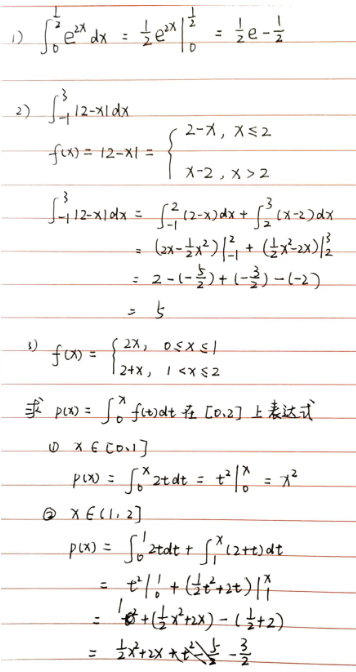
5.3.1 定积分的换元积分法
-
在使用换元积分法解定积分时
- 新元 \(x=\phi(t)\),\(\phi(t)\) 必须在被积区间 \([a, b]\) 上单调
- 上下限也变,原变量上(下)限与新变量上(下)限互相对应
-
奇偶函数被积区间关于原点对称的定积分
\(f(x)\) 是偶函数,\(\int_{-a}^{a}f(x)dx=2\int_{0}^{a}f(x)dx\)
\(f(x)\) 是奇函数,\(\int_{-a}^{a}f(x)dx=0\)
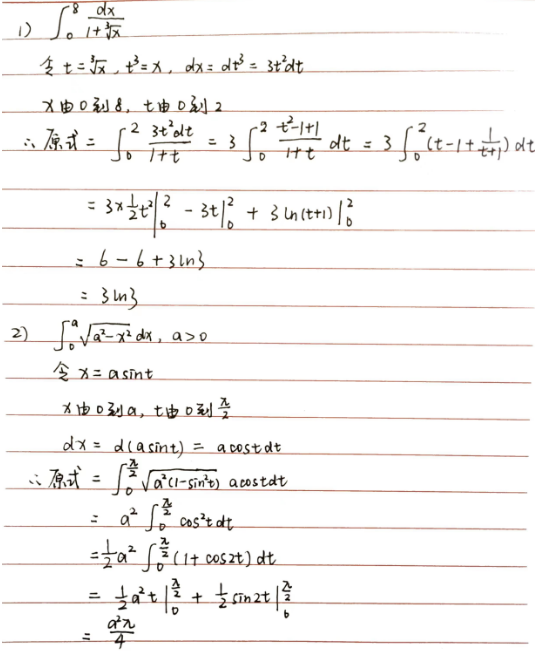

5.3.2 定积分的分部积分法
(定积分的分部积分+上下限)
\(\int_{a}^{b} udv=uv|_{a}^{b}-\int_{a}^{b}vdu\)
同样遵循反(三角函数)对(数函数)幂(函数,多项式型)三(角函数)指(数函数)的规律决定 \(u\) 与 \(v\)
5.4 定积分的应用
-
求面积
\(\int_{a}^{b}(f(x)-g(x))dx\)
想象一把 "量尺":由 \(x\) 轴或 \(y\) 轴开始平移 (有时需要将 \(f(x),g(x)\) 变换成以 \(y\) 为自变量的函数) -
求体积
\(\int_{a}^{b}A(x)dx\):\(A(x)\) 是物体的横截面积
(面积是积点成面,体积是积面成体) -
经济问题
5.5.1 广义积分-无穷限积分
-
广义无穷限积分
\(\int_{a}^{+\infty}f(x)dx=\lim \limits_{b\to +\infty} \int_{a}^{b}f(x)dx\)
\(\int_{-\infty}^{b}f(x)dx=\lim \limits_{a\to -\infty} \int_{a}^{b}f(x)dx\)
\(\int_{-\infty}^{+\infty}f(x)dx=\int_{-\infty}^{c}f(x)dx+\int_{c}^{+\infty}f(x)dx\) -
广义牛顿-莱布尼茨定理 (由 \(1\) 推出)
\(\int_{0}^{+\infty}f(x)dx=F(x)|_{0}^{+\infty}=F(+\infty)-F(0)\)
\(\int_{-\infty}^{0}f(x)dx=F(x)|_{-\infty}^{0}=F(0)-F(-\infty)\)
\(\int_{-\infty}^{+\infty}f(x)dx=F(x)|_{-\infty}^{+\infty}=F(+\infty)-F(-\infty)\) -
性质
- 广义无穷限积分可能是发散的
- 若 \(\int_{a}^{+\infty}f(x)dx\) 收敛,则 \(\int_{a}^{+\infty}kf(x)dx\) 收敛
- 若 \(\int_{a}^{+\infty}f(x)dx\) 与 \(\int_{a}^{+\infty}g(x)dx\) 收敛,则 \(\int_{a}^{+\infty}(f(x)\pm g(x))dx\) 收敛
- 换元积分法,分部积分法都可以应用在广义无穷限积分上
-
广义积分的收敛判定
- 法一 (单调有界必收敛):
若 \(f(x)\geq 0\),则 \(\int_{a}^{+\infty}f(x)dx\) 收敛 \(\iff\) \(p(x)=\int_{a}^{x}f(t)dt\) 有界 (注意 \(p'(x)=f(x)\)) - 法二 (比较判敛法):
若 \(0\leq f(x) \leq g(x)\):
1)\(\int_{a}^{+\infty}g(x)dx\) 收敛,则 \(\int_{a}^{+\infty}f(x)dx\) 收敛
2)\(\int_{a}^{+\infty}f(x)dx\) 发散,则 \(\int_{a}^{+\infty}g(x)dx\) 发散 - 法三 (绝对收敛必收敛):
\(\int_{a}^{+\infty}|f(x)|dx\) 收敛 \(\to \int_{a}^{+\infty}f(x)dx\) 收敛
严谨证明:因为有 \(0 \leq f(x)-|f(x)| \leq 2|f(x)|\) (分类讨论 \(x\) 的符号可证)
应用比较判敛法 \(\int_{a}^{+infty} 2|f(x)|dx\) 收敛,则 \(\int_{a}^{+infty} (f(x)-|f(x)|)dx\) 收敛
再应用性质 \(3\) 推出 \(\int_{a}^{+\infty}f(x)dx\) 收敛
- 法一 (单调有界必收敛):
-
应用比较判敛法的一个例题

5.5.2 广义积分-瑕积分
-
瑕积分
瑕积分是指被积函数带有瑕点的广义积分:瑕点是被积区间中没有定义的点
若在被积区间 \([a, b]\) 中:
\(a\) 点无定义:\(\int_{a}^{b} f(x)dx=\lim \limits_{\xi^{+} \to 0} \int_{a+\xi^{+}}^{b}f(x)dx\)
\(b\) 点无定义:\(\int_{a}^{b} f(x)dx=\lim \limits_{\xi^{+} \to 0} \int_{a}^{b-\xi^{+}}f(x)dx\)
\(\exist c \in (a, b)\),\(c\) 点无定义,\(\int_{a}^{b} f(x)dx=\int_{a}^{c} f(x)dx+\int_{c}^{b}f(x)dx\),转化为上面的两种情况 -
例题

-
伽马函数
伽玛函数 (无穷限积分):\(\Gamma (r)=\int_{0}^{\infty}x^{r-1}e^{-x}dx (r>0)\)
注意:伽马函数的定义域是 \(r>0\),在定义域上连续
伽玛函数的性质:\(\Gamma(r+1)=r \Gamma(r) (r>0)\),所以当 \(n\in N^{+}\) 时有 \(\Gamma(n+1)=n!\)
可以看出,伽玛函数是阶乘函数在实数与复数上扩展的一类函数
6.1 空间解析几何
空间直角坐标系(右手系),空间两点间距离公式
二元函数 \(\to\) 曲线,三元函数 \(\to\) 曲面
平面方程:\(Ax+By+Cz+D=0\),且 \(A, B, C\) 不全为 \(0\) (如果全为\(0\),点集不是平面,而是整个空间)
球面方程:\(\sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}=R\)。若球心是原点,则 \(x^2+y^2+z^2=R^2\)
柱面:准线(某段曲线)沿着母线平行移动所形成的曲面为柱面。例:\(x^2+y^2=0\) (以 \(z\) 轴为中心的圆柱面)
旋转抛物面:某段抛物线旋转形成的曲面。例:\(x^2+y^2=z\),沿 \(z\) 轴方向的切面均为抛物线
鞍面(双曲抛物面):某段双曲线旋转形成的曲面。例 \(y^2-x^2=z\),沿 \(z\) 轴方向的切面为抛物线,沿 \(x\) 或 \(y\) 轴方向的切面为双曲线
6.2 多元函数的基本概念
-
一些概念在多(三)元函数上的延申
邻域 \(U(P_0,\xi)=\{(x, y)|\sqrt{(x-x_0)^2+(y-y_0)^2}<\xi\}\), 去心邻域 \(U(P_0,\xi)=\{(x, y)|0<\sqrt{(x-x_0)^2+(y-y_0)^2}<\xi\}\)
曲面的内点(一定存在其的一个邻域完全在曲面中)边界点(边界点的邻域全都一部分在曲面内,一部分在曲面外)
曲面是开集(类比开区间,排除边界点),闭区域(类比闭区间,包括边界点)
曲面的有界(有边界,被围起来)与无界 -
多元函数的几何意义
-
多元函数的极限存在条件
回忆一元极限:函数 \(f(x)\) 在 \(x=x_0\) 处的极限,要求分别从左右两侧向 \(x_0\) 逼近的极限相等 \(\lim \limits_{x\to x_0^{-}}f(x)=\lim \limits_{x\to x_0^{+}}f(x)(=f(x_0))\)
而对于二元函数 \(f(x, y)\) 在 \(x=x_0, y=y_0\) 处的极限,要求从任意方向 向 \(x=x_0, y=y_0\) 逼近的极限都相等;反之在该处极限不存在
-
求二元函数的极限
方法仍然采用一元函数极限的相关方法:重要极限,等价无穷小,有界 \(\times\) 无穷小 \(=\) 无穷小
注意:二元函数极限不能使用洛必达法则

-
二元函数的连续性
回忆一元函数的连续性:函数 \(f(x)\) 在 \(x_0\) 上连续意味着:
1)函数在 \(x=x_0\) 处有定义
2)函数在 \(x=x_0\) 处有极限 \(\lim \limits_{x\to x_0}f(x)\)
3)函数在 \(x=x_0\) 处的函数值与极限相等 \(\lim \limits_{x\to x_0}f(x)=f(x_0)\)
二元函数的连续性定义与一元函数一致:在 \(x=x_0, y=y_0\) 处有定义,有极限,定义与极限相等
6.3 偏导数
-
偏导数
一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定
回忆一元函数的导数定义:\(\lim \limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim \limits_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\)
对于二元函数 \(z=f(x, y)\)
其对 \(x\) 求偏导 (\(y\) 不变):\(\lim \limits_{\Delta x \to 0} \frac{\Delta_{x} z}{\Delta x}=\frac{f(x_0+\Delta x, y_0)-f(x_0, y_0)}{\Delta x}\)
其对 \(y\) 求偏导 (\(x\) 不变):\(\lim \limits_{\Delta y\ to 0} \frac{\Delta_{y} z}{\Delta y}=\frac{f(x_0, y_0+\Delta y)-f(x_0, y_0)}{\Delta y}\)
关于求偏导的相关题目:对某变量 (例如 \(x\)) 求偏导,则将其他变量 (\(y, z, ...\)) 视为常数直接求导即可 -
偏导数和多元函数连续型
回忆对于一元函数:可导必连续 (见微积分 I - 2.1.2 - 3)
然而对于多元函数:偏导存在不一定连续 (这是因为偏导数只求多元函数在某个方向上的导数,而连续要求多元函数在每个方向上的导数都存在) -
偏导数的几何意义
对 \(x\) 求偏导:曲面与 \(x-z\) 平面相平行的面相截的曲线的导数
对 \(y\) 求偏导:曲面与 \(y-z\) 平面相平行的面相截的曲线的导数
\(...\) -
二阶偏导数
\(\frac{\partial}{\partial x} (\frac{\partial z}{\partial x})=\frac{\partial^2 z}{\partial x^2}=z_{xx}^{''}=f_{xx}^{''}(x, y)\)
类似的,还有 \(f_{yy}^{''}(x, y)\) 二阶混合偏导数 \(f_{xy}^{''}(x, y), f_{yx}^{''}(x, y)\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号