1.1 集合
这一节复习了高中关于集合的基础知识
介绍了一些新的概念
-
笛卡尔积 (Cartesian Product)
集合 X 与 Y 的笛卡尔积 (直积) X×Y 是指包含了所有第一个成员属于 X,第二个成员属于 Y 的所有有序对的集合
A×B={(x,y)|x∈A,y∈B}
-
邻域 (neignbourhood)
点 a 的 δ (δ>0)邻域:
指开区间 (a−δ,a+δ),也即 U(a,δ)={x||x−a|<δ}
-
去心邻域
点 a 的 δ(δ>0) 的去心邻域 (即不包括点 a):
U0(a,δ)={x|0<|x−a|<δ} (去心标记方式是 U 上写一个小 0)
1.2 函数
1.3 数列极限 I
-
引入
对于无限数列 an=nn+1,an→1 (趋近于 1)
关于 0.9999...=1
-
数列极限的定义
对于 {xn},若 ∃a,∀ϵ>0,都 ∃N,使得对于所有 n>N 的 xn 都满足 |xn−a|<ϵ
那么我们就称 a 为 {xn} 的极限 (或 {xn} 收敛于 a),也即 limn→+∞xn=a
这个定义的几何理解:对于以极限 a 为中心,以任意常数 ϵ 为半径的邻域,一定能够找到数列中的某一项 aN,使得这一项之后的所有项的取值全部落在该邻域内
-
证明数列的极限 (即找到存在的 N)

1.4 数列极限 II
- 若 {xn} 收敛,则其极限唯一
- 若 {xn} 收敛,其有界
- 有界是收敛的必要条件 (即收敛必有界,有界不一定收敛,例 {1,−1,1,−1,1...})
- 若数列单调有界,则必收敛
- limn→∞xn=a(a>0),∃N,n>N,xn>0
- 子数列:与子集的区别:子数列中项的相对顺序与原数列一致
- 若某数列收敛于 a,则其子数列也收敛于 a
- 若找到某个子数列不收敛,则原数列一定发散
- 若找到两个子数列收敛,但其极限不同,则原数列不收敛 e.g.{1,−1,1,−1,1,...}
- 原数列收敛的充要条件:其奇数项子数列与偶数项子数列均收敛,且极限相同
1.5 函数极限 I
-
函数极限 (趋近正无穷)
当 x→+∞ 时,若 ∃a,∀ϵ,∃X,使得 x>X 时,|f(x)−a|<ϵ
则我们称函数趋近正无穷时极限为 a,即 limx→+∞f(x)=a
-
函数极限 (趋近负无穷)
-
函数极限 (趋近无穷(正&&负))
当 x→∞ 时,若 ∃a,∀ϵ,∃X(X>0), 使得 |x|>X 时,|f(x)−a|<ϵ
则 limx→∞f(x)=a
-
函数极限 (趋近某个有限值 x0)
当 x→x0 时,若 ∃a,∀ϵ,∃δ>0,使得 0<|x−x0|<δ 时,|f(x)−a|<ϵ
则 limx→x0=a
注意:由于 x 是趋近 x0,所以在讨论时 x 是取不到 x0 的。因此,f(x) 在 x0 处可以没有定义,只需要在 x0 的去心邻域内有定义即可
-
左极限与有极限
- 左极限 (即趋近点 x0 的左侧的极限,x<x0):以 x→x−0 表示
- 右极限 (即趋近点 x0 的右侧的极限,x>x0):以 x→x+0 表示
- 左右极限定理:limx→x0f(x)=a⟺limx→x−0f(x)=limx→x+0f(x)=a
- 推论1:若左(右)极限不存在,则 x→x0 极限不存在
- 推论2:若左右极限均存在但极限不相等,则 x→x0 极限不存在
-
函数极限的几何理解:
以极限 a 为中心,任意 ϵ 为半径的邻域一定能够 "框住" 由某处 x=X 开始到无穷 (正或负) 的所有函数图像
若讨论函数趋近某个定值 x0 的极限时,则是以极限 a 为中心,任意 ϵ 为半径的邻域一定能够 "框住" 某个以 x0 为中心的去心邻域范围所对应的函数图像
1.5 函数极限 II
- 唯一性:若极限存在,则在该点的极限是唯一的
- 局部有限性:若趋近于 x0 的极限存在,则一定存在 x0 的去心邻域,函数在该范围内有界
- 局部保号性:若 limx→x0f(x)=a(a>0),则一定存在 x0 的去心邻域,函数在该范围内大于 0
- 取函数 f(x) 的一系列值形成数列 {xn}: 若 limx→x0f(x)=a,则 limx→x0{xn}=a
- 推论1:若 ∃{xn} 极限不存在,则原函数极限不存在
- 推论2:若 ∃{xn},{yn} 极限存在但不相等,则原函数极限不存在
- f(x)=a+α(x),limx→x0α(x)=0,则 limx→x0f(x)=a
1.6 无穷小与无穷大
-
无穷小
无限趋近于 0
limx→x0f(x)=0 此时 f(x) 即是 x→x0 的无穷小
- 无穷小 +/−/× 无穷小仍是无穷小
- 无穷小 × 有界仍是无穷小
- 无穷小 ÷ 无穷小可能是:常数,无穷大 (∞),无穷小 (0)
-
无穷大
即 +∞ 与 −∞
- 无穷大 × 无穷大仍是无穷大 (注意符号判断)
- 无穷大 + 有界仍是无穷大
- 无穷大 +/− 无穷大可能是:常数,无穷大 (∞),无穷小 (0)
1.7 极限的运算法则
-
四则运算
若 limf(x)=a,limg(x)=b (对所有的变化过程都成立)
- lim(f(x)±g(x))=limf(x)±limg(x)
- lim(f(x)g(x))=limf(x)×limg(x)
- limf(x)g(x)=limf(x)limg(x)(b≠0)
-
常数和与 x 无关的变量 可以提出极限外
- limc⋅f(x)=climf(x)
- limyf(x)=ylimf(x) (y 与 x 无关)
- 幂:limf(x)n=(limf(x))n
-
分配律:两个条件:是有限个函数且每个函数存在极限
lim(f1(x)+f2(x)+...+fN(x))=limf1(x)+limf2(x)+...+limfN(x),N 为有限的
-
复合函数求极限
对于复合函数 u=ϕ(x),y=f(u)
limx→x0f[ϕ(x)]=f[limx→x0ϕ(x)]
-
limu(x)v(x)
limu(x)=a,limv(x)=b 则 limu(x)v(x)=ab
证:limu(x)v(x)=limelnu(x)v(x)=limev(x)lnu(x)
根据复合函数求极限法则
limev(x)lnu(x)=elimv(x)lnu(x)=elimv(x)ln(limu(x))=eblna=elnab=ab
-
求函数极限的相关题目
limx→a=...,... 为:
- 多项式或普通的有理分式:直接将 x=a 代入,极限可能是常数,0 或 ∞
- 代入后 ∞∞ 型:
若分子分母次数相同:极限为 最高次的系数之比
若分母次数大于分子次数:极限为 0
若分子次数大于分母次数:极限为 ∞
- 代入后 00 型:
分子/分母有理化、洛必达法则:极限可能是常数,0 或 infty
- 无限项之和
例:求 limn→∞(1n2+2n2+...+nn2) 的极限
注意:这里 n→∞ ,所以后面的项是无限的,不能使用分配律将极限拆开
所以 limn→∞(1n2+2n2+...+nn2)=limn→∞12n(n+1)n2=12
1.8.1 极限的存在准则
-
夹逼定理
对于函数 f(x),g(x),h(x)
满足对于 U(x0,r) (x0 的半径为 r 的去心邻域),g(x)≤f(x)≤h(x)
若 limx→x0g(x)=h(x)=a,则 limx→x0f(x)=a
- 例:求 limn→∞2nn!
0<2nn!=21×2×2×..22×3×...(n−1)×2n<4n (小小的放缩)
又 limn→∞0=limn→∞4n=0
根据夹逼定理 limn→∞2nn!=0
-
单调有界数列必有极限
即:单调增有上界数列必有极限;单调减有下界数列必有极限 (一定会增/减到接近界,所以必有极限)
- 例:a>0,x1=√a,xn=√a+xn−1
√a<√a+√a,即 x1<x2
对于 xn−1<xn
a+xn−1<a+xn
√a+xn−1<√a+xn
xn<xn+1
所以数列单调递增
x1=√a<√a+1
对于 xn<√a+1
xn+1=√a+xn<√a+√a+1<√a+2√a+1=√(√a+1)2=√a+1
所以数列存在上界 √a+1
综上述,数列存在极限。设 limn→∞{xn}=b
xn=√a+xn−1
limn→∞{xn}=limn→∞√a+xn−1
limn→∞{xn}=√limn→∞(a+xn−1)
b=√a+b
解出该式即可求出极限 b
1.8.2 两个重要极限
-
limx→0sinxx=1
高中知识:y=sinx 与 y=x 在 x0=0 处的导数相等
推论:limx→0sinαxx=α (将 αx 看成整体并配成原式)
-
e 的定义:limn→∞(1+1n)n=e
- 例:求 limx→+∞=(1−1x)√x
=limx→∞(1+1√x)√x(1−1√x)√x
=limx→∞(1+1√x)√x[(limx→∞(1+1−√x))−√x]−1
=e×1e
=1
1.9 无穷小的比较
-
limf(x)=0,limg(x)=0,g(x)≠0
- limf(x)g(x)=0,则 f(x) 是 g(x) 的高阶无穷小,记为 f(x)=o(g(x))
- limf(x)g(x)=∞,则 f(x) 是 g(x) 的低阶无穷小
- limf(x)g(x)=c(c≠0),则 f(x) 是 g(x) 的同阶无穷小
若 c=1,f(x) 是 g(x) 的等价无穷小,记为 f(x)∼g(x)
下面的 2∼6 将会给出 4 个常用的等价无穷小对,做题时可以进行替换简化计算
-
ln(1+x)∼x,x→0
-
ex−1∼x,x→0
推论:ax−1∼xlna,x→0
-
n√1+x−1∼1nx,x→0
这个结论证明比较难,先引入一个式子(易知成立):an−1=(a−1)(an−1+an−2+...+a+1)
∴a−1=an−1(a−1)(an−1+an−2+...+a+1
直接将 n√1+x=(1+x)1n 看作 a 并代入上式
(1+x)1n−1=(1+x−1)((1+x)n−1n+(1+x)n−2n+...+(1+x)1n+1)
∴limx→0x((1+x)n−1n+(1+x)n−2n+...+(1+x)1n+1)xn=nlimx→0((1+x)n−1n+(1+x)n−2n+...+(1+x)1n+1)n×1n=1
注:n 一定是有穷的,n 若无穷极限的分配律不成立
-
sinx∼x,tanx∼x,x→0
-
若 f1(x)∼f2(x),g1(x)∼g2(x) 且存在 limg2(x)f2(x),则 limg1(x)f1(x)=limg2(x)f2(x)
- 只有两个无穷小之比才可以进行替换
- 若分子或分母是若干个因子的乘积,可以仅对部分的因子进行无穷小替换
-
例题 (均是 00 型)
- limx→0sin2xx3+3x
=limx→02xx3+3x=limx→02x2+3=23 (利用了 sinx∼x,x→0)
- limx→0(ex−1)sinx1−cosx
=limx→0x×x2sin2x2
=limx→0x×x2×x24=2
1.10.1 函数的连续性 I
-
增量(改变量)
Δx (自变量增量)
Δy=f(x0+Δx)−f(x0) (因变量增量)
注:增量可以为负
-
函数在 x=x0 处连续的定义
f(x) 在 x0 的邻域内有定义 (注意是邻域而非去心邻域,这意味着 x=x0 时不一定需要有定义)
定义一:limΔx→0Δy=limΔx→0[f(x0+Δx)−f(x0)]=0
定义二:limx→x0f(x)=f(x0)
这些定义均包含三个条件:
- 在 x0 处有定义
- x→x0 f(x) 有极限
- 极限 =f(x0)
-
关于左连续与右连续
若 x0 的右侧/左侧没有定义,则取 x0 的左邻域/右邻域
-
在区间上连续
区间 [x1,x2]
在区间内部 (x1,x2),连续
在 x=x1 时右连续
在 x=x2 时左连续
-
关于间断点 (不连续)
- 无穷间断
不满足条件一:即在 x→x0 时无定义
例,对于函数 y=1x,x=0 即是其的无穷间断点
- 震荡
不满足条件二:即 x→x0 时 f(x) 无极限
- 跳跃
不满足条件三:即极限不等于 f(x0)
- 可去
同样不满足条件三:即极限不等于 f(x0)
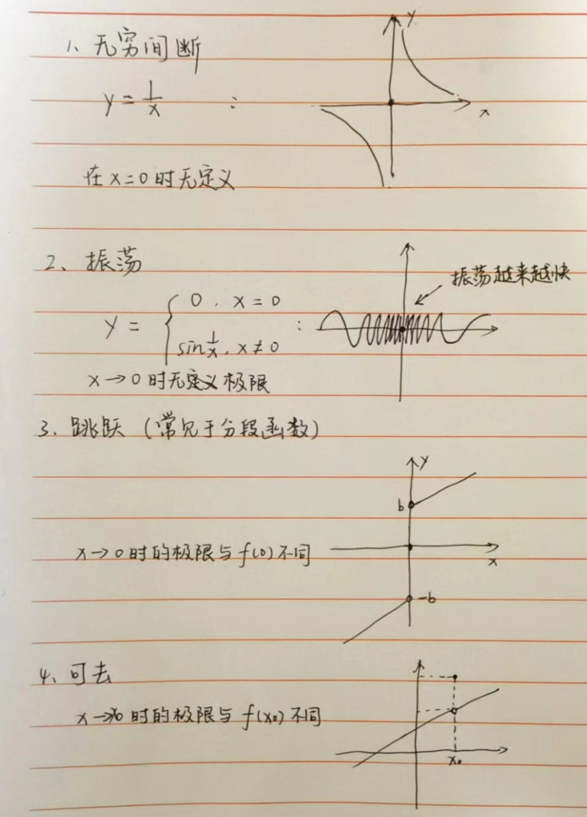
跳跃间断与可去间断属于第一类:当 x→x0 时左右极限均存在
而无穷间断与震荡间断属于第二类:左右极限不存在
- 连续的几何解释:一笔画
1.10.2 函数的连续性 II
-
函数运算对连续性的影响
f(x),g(x) 均为连续函数
四则运算:f(x)±g(x),f(x)×g(x),f(x)g(x)(g(x)≠0) 得出的新函数仍连续
多项式:a0xn+a1xn−1+...+an−1x+an 一定在 (−∞,+∞) 上连续
复合函数:u=ϕ(x),y=f(u) 均连续,复合函数 f(ϕ(x)) 也连续
反函数:y=f(x) 连续并是单调函数,那么它的反函数也一定连续(注意,这里的单调条件是为了保证函数存在反函数)
-
闭区间上连续的性质
- 有界性:在 [a,b] 上连续,函数值一定有界
- 最值性:在 [a,b] 上连续,函数一定有最大/最小值
- 介值性:在 [a,b] 上连续,函数的最大值为 M,最小值为 m,∀c(m<c<M),闭区间内一定存在 ϵ 使得 f(ϵ)=c
- 零点存在定理:在 [a,b] 上连续,若 f(a)f(b)<0,则在 (a,b) 内一定存在至少一个零点 (即函数值为 0 的点)
2.1.1 导数的定义 I
-
导数:用于描述函数的平均变化率(在 x=x0 处切线的斜率)
y=f(x) 在 U(x0) 有意义
x0→x0+Δx,f(x0)→f(x+x0),则函数在 x=x0 处的导数为 limΔx→0f(x0+Δx)−f(x0)Δx
-
其他表述
limΔx→0ΔyΔx
limx→x0f(x)−f(x0)x−x0
-
利用导数的定义解题
例:y=x2 求 y′|x=2
x→x+Δx,f(x)→f(x+Δx)
Δy=f(x+Δx)−f(x)=2xΔx+(Δx)2
y′|x=2=limΔx→0ΔyΔx=limΔx→0(2x+Δx)=2x=4
-
常见函数的导函数
y=c,y′=0
y=xn,y′=nxn−1 (n 为整数)
y=xa,y′=axa−1
y=sinx,y′=cosx
y=cosx,y′=−sinx
y=lnx,y′=1x
y=logax,y′=1xlna
y=ax,y′=axlna
y=ex,y′=ex
2.1.2 导数的定义 II
-
导数的意义 limx→x0ΔyΔx
- y=f(t) 时间-路程函数,f′(t) 表示瞬时速度
- 在 x=x0 处切线的斜率
- 切线方程:y−y0=f′(x0)(x−x0)
法线方程:y−y0=1f′(x0)(x−x0)
-
关于单侧导数
在有定义的区间 [a,b] 上
在 x=a 时右可导,其右导数记为 f′+(a)
在 x=b 时左可导,其左导数记为 f′−(b)
在区间内部函数可导,其充要条件为 左右导数均存在且相等 (该结论一般用于证明某点是否可导)
例:对于 y=|x|,讨论在 x=0 时是否可导
f+(0)=limΔx→o+f(0+Δx)−f(0)Δx=limΔx→0+ΔxΔx=1
f−(0)=limΔx→o−f(0+Δx)−f(0)Δx=limΔx→0−−ΔxΔx=−1
∴f+(0)≠f−(0)
在 x=0 处函数不可导
-
可导与连续的关系
可导的几何意义:函数图像是光滑的
连续的几何意义:函数图像可一笔画
光滑的图像必能被一笔画,而可一笔画的图像不一定光滑(y=|x|) ⟺ 可导一定连续,连续不一定可导
证明:
可导意味着 limΔx→0ΔyΔx 存在
连续意味着 limΔx→0Δy=0
可导必连续:limΔx→0Δy=limΔx→0(ΔyΔxΔx)=limΔx→0ΔyΔxlimΔx→0Δx=0
2.2 求导法则
-
(u(x)+v(x))′=u′(x)+v′(x)
(u1(x)+u2(x)+...+un(x))′=u′1(x)+u′2(x)+...+u′n(x)
-
(u(x)v(x))′=u′(x)v(x)+u(x)v′(x)
(cu(x))′=cu′(x)
(u(x)v(x)w(x))′=u′(x)v(x)w(x)+u(x)v′(x)w(x)+u(x)v(x)w′(x)
-
(u(x)v(x))′=u′(x)v(x)−u(x)v′(x)v2(x)
-
反函数的导数互为倒数
y=f(x),x=ϕ(y) 那么 f′(x)=1ϕ′(y)
例:求 y=ax 的导数
x=logay(y>0)
则 (ax)′=1(logay)′=ylna=axlna
-
复合函数求导链式法则
y=f(u),u=ϕ(x)
dydx=dydu⋅dudx
(f(ϕ(x)))′=f′(u)⋅ϕ′(x)
例:求 f(x)=esin21x 的导数
f′(x)=esin21x⋅2sin1x⋅cos1x⋅(−1x2)
2.4 高阶导数
-
二阶导数
y′′=ddydxdx=d2ydx2 (注意指数的位置)
y′′′ (三阶导数)
y(4) (四阶导数)
-
隐函数求导
对于 x2+y2=r2,求 d2ydx2
两边同时对 x 求导:2x+2y⋅dydx=0 (第二项是复合函数求导)
dydx=−xy (再两边同时对 x 求导得到二阶导数)
d2ydx2=−y−xdydxy2=−y+x2yy2=−y2+x2y3=−r2y3 (将 dydx=−xy 代入)
-
参数方程求导
x=a(t−sint),y=a(1−cost),求 d2ydx2
dydx=dydtdxdt=sint1−cost
∴ddx(dydx)=ddx(sint1−cost)=ddt(sint1−cost)1dxdt=−1a(cost−1)2 (用到了反函数求导以及复合函数求导链式法则)
讲一下自己对式子的理解:函数 f(t) 对 x 求导,而 t=ϕ(x),则 f(ϕ(x))=f′ϕ′,ϕ′ 通过 x=a(t−sint) 的反函数求导法则得出
-
一些常见函数的高阶导数
- (u±v)(n)=u(n)±v(n)
- (cu)(n)=cu(n)
- (uv)(n)=∑ni=0Cinu((n−i))v(i)
- (sinx)(n)=sin(x+nπ2)
- (cosx)(n)=cos(x+nπ2)
2.5.1 微分I
-
微分(dy)是函数改变量(Δy)的线性主要部分
f(x) 在 x0 邻域内有定义,x0+Δx 在邻域内
若 Δy=f(x0+Δx)−f(x0) 可以表示为 Δy=AΔx+o(Δx) (A 是与 Δx 无关的常数,o(Δx) 是 Δx 的高阶无穷小)
则我们称 f(x) 在 x0 可微,其微分 dy=AΔx
(Δy 是函数改变量的精确值,dy 是其的近似值)
-
一元函数在 x0 可微 ⟺ 可导
dy=f′(x0)Δx=f′(x0)dx
这里是证明
所以,定义中的常数 A 即是 f(x) 在 x0 处的导数
-
微商(即导数)
将 dy=f′(x)dx 式子转变一下即得到求导公式 f′(x)=dydx
在一元函数内导数就是微分的分数形式
-
微分的几何意义
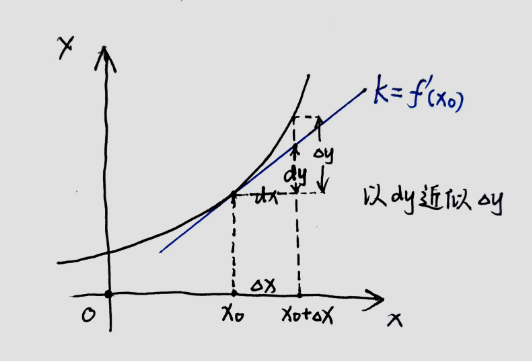
2.5.2 微分II
-
微分基本公式:dy=f′(x)dx
-
四则运算
dc=c′dx=0
d(u±v)=du±dv
d(cu)=cdu
d(uv)=vdu+udv
d(uv)=(uv)dx=u′v−v′uv2dx=vdu−udvv2
(对于分式求微分的相关题目,若分子次数大于等于分母,可以配成 x...+cx... 的形式再求微分)
-
一阶微分的形式不变性
对于 y=f(u)
- 若 u 为自变量,dy=f′(u)du
- 若 u 为函数 u=ϕ(x),则 dy=y′xdx=f′(u)(ϕ′(x)dx)=f′(u)du
-
隐函数求微分
例:对于 x2+2xy−y2=2x 求 dy
- 方法一:等式两边同时对 x 求导
x+y+xy′−yy′=1
∴y′=1−x−yx−y,dy=y′dx=1−x−yx−ydx
- 方法二:等式两边同时求微分
xdx+xdy+ydx−ydy=dx
-
微分的应用
因为 Δy≈dy=f′(x0)dx
所以 f(x0+Δx) 可由 f(x0)+f′(x0)Δx 近似得出 (|Δx| 取很小)
-
等价无穷小的推出
还记得上面的几个等价无穷小的结论(1.9-2)吗?它们可以由上式推导而来
取 x0=0,Δx=x 则有 f(x)≈f(0)+f′(0)x
这个式子同样可以用于近似计算 (当且仅当 x 很小的时候可以近似!)
3.1.1 微分中值定理
-
费马引理
f(x) 在 x0, U(x0) 处有定义且在 x0 处可导
若 f(x)≤f(x0) (或 f(x)≥f(x0)) 则 f′(x0)=0
非常符合直觉的结论,下面是证明 (f(x)≤f(x0)的情况)
f′−(x0)=limx→0−f(x0+Δx)−f(x0)Δx≥0 (分子小于等于 0, 分母小于 0)
f′+(x0)=limx→0+f(x0+Δx)−f(x0)Δx≤0 (分子小于等于 0, 分母大于 0)
又 f(x) 在 x0 处可导,所以 f−(x0)=f+(x0)=0
-
罗尔中值定理
若 f(x) 满足:1. 在 [a,b] 上连续 2. 在 (a,b) 上可导 3. f(a)=f(b)
则至少存在一个 ξ∈(a,b),使得 f′(ξ)=0
-
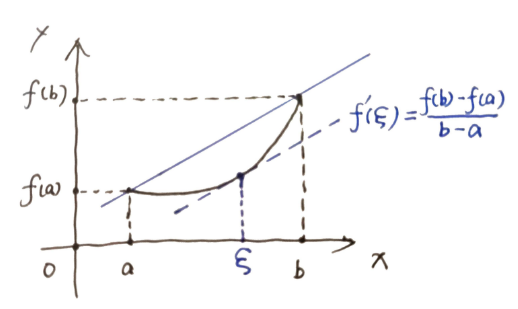
拉格朗日中值定理
若 f(x) 满足:1. 在 [a,b] 上连续 2. 在 (a,b) 上可导
则至少存在一个 ξ∈(a,b) 使得 f′(ξ)=f(b)−f(a)b−a
罗尔中值定理是拉格朗日中值定理在 f(a)=f(b) 时成立的情况
3.1.2 柯西中值定理
若 f(x)和F(x) 满足:1. 在 [a,b] 上连续 2. 在 (a,b) 上可导 3. ∀x∈(a,b), F′(x)≠0
则至少有一点 ξ 使得 f(b)−f(a)F(b)−F(a)=f′(ξ)F′(ξ)
拉格朗日中值定理是柯西中值定理在 F(x)=x 时成立的情况
这里 用构造函数法+罗尔中值定理对柯西中值定理进行了证明
3.1.3 泰勒定理
-
介绍
泰勒公式,是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定的条件,泰勒公式可以用函数在某一点的n阶导数值做系数构建一个n次多项式来近似表达这个函数
之前介绍的近似公式 f(x)≈f(x0)+f′(x0)(x−x0) 用某点的信息以 一次多项式 的形式描述附近函数的取值,误差可能较大
-
泰勒定理
f(x) 可以表示成 x−x0 的 n 次多项式加余项 Rn(x)
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+...+f(n)(x0)n!(x−x0)n+Rn(x)
拉格朗日型余项 Rn(x)=f(n+1)(ξ)(n+1)!(x−x0)(n+1),ξ∈(x0,x)
拉格朗日余项实际是泰勒公式展开式与原式之间的一个误差值,如果其值为无穷小,则表明公式展开足够准确
-
麦克劳林公式
泰勒公式在 x0=0 时成立的情况,即
f(x)=f(0)+f′(0)1!x+f′′(0)2!x2+...+f(n)(0)n!xn+Rn(x)
例:将函数 f(x)=ex 使用麦克劳林公式展开 (f(n)(0)=e0=1)
ex=1+x1!+x22!+...+xnn!+eθx(n+1)!xn+1,其中 f(n+1)(ξ)=eξ=eθx
∴ex≈x+x22!+...+xnn!
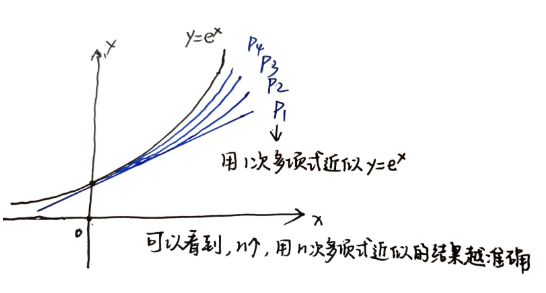
另:类似的,sinx≈=x−13!x3+15!x5−...+(−1)m−1(2m−1)!x2m−1+R2m
3.2 洛必达法则
-
公式介绍
若函数 f(x),g(x) 满足
(1)limx→x0f(x)=limx→x0g(x)=0 (00 型)
(2) 在 x0 的去心邻域内可导且 g′(x)≠0
(3) limx→x0f′(x)g′(x)=a (或者 ∞)
则 limx→x0f(x)g(x)=limx→x0f′(x)g′(x)=a (或者 ∞)
-
使用柯西中值定理进行证明
首先可以发现,洛必达法则对 f(x) 与 g(x) 在 x0 处的定义有无并不做要求
不如令 f(x0)=g(x0)=0 (这一步是为了满足应用柯西中值定理的条件)
此时,f(x),g(x) 在 x0 处定义,极限均存在且相等 (limx→x0f(x)=f(x0)=0)
∵ x 在 x0 的去心邻域内,f(x),g(x) 在区间 [x0,x] 可导
对 f(x),g(x) 应用柯西中值定理,则有
∃ξ∈(x0,x) 使得 f(x)−f(x0)g(x)−g(x0)=f(x)−0g(x)−0=f(x)g(x)=f′(ξ)g′(ξ)
∵limx→x0f(x)g(x)=limx→x0f′(ξ)g′(ξ)
又 ξin(x0,x),x→x0,∵ξ→x0 (可以将 x0 理解为定值,x 在 x0 的去心邻域内移动)
最终有 limx→x0f(x)g(x)=limx→x0f′(ξ)g′(ξ)=limξ→x0f′(ξ)g′(ξ)=limx→x0f′(x)g′(x)
-
洛必达法则的适用范围
不定式极限:
lim00: 已证明,见上
lim∞∞=lim1∞1∞=lim00
lim0⋅∞=lim1∞⋅∞=lim∞∞
lim00=limeln00=elim0ln0=elim0⋅∞
lim1∞=limeln1∞=elim∞ln1=elim0⋅∞
lim∞0=limeln∞0=elim0ln∞=elim0⋅∞
-
例题

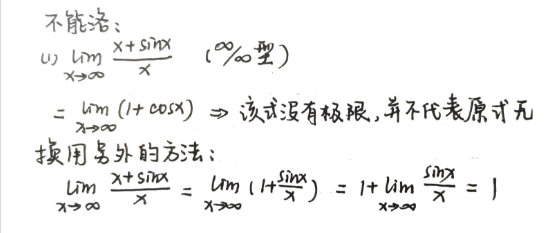
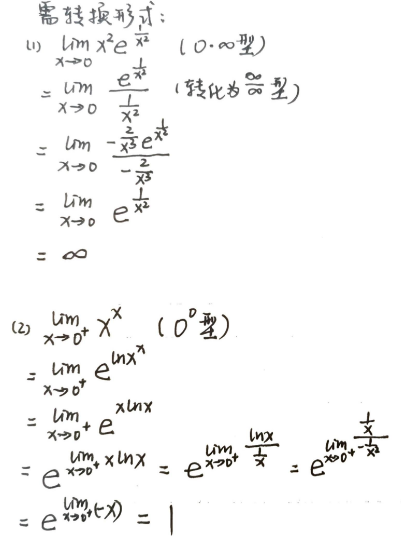
运用洛必达法则解题时注意以下几点:
- 要符合不定式条件 (如 00,∞∞)
- 结合重要极限,等价无穷小替换等方法简化计算
- 若 limf′(x)g′(x) 不存在也不等于 ∞ 时,不能断言原式 limf(x)g(x) 也不存在。应当采用洛必达以外的方法进行解题
3.3 函数单调性与凹凸性
-
单调性
单调递增 f′(x)>0 递减 f′(x)<0 (若 f′(x)≥0,则等号只能在个别点成立)
函数的分界点(函数单调性发生改变的点):驻点 (f′(x)=0 的点),导数不存在的点 (这是一个充分不必要条件)
当解答关于分析函数单调性的相关题目时,研究函数的导数,先找到函数分界点,再对各个区间进行分段讨论
例:分析函数 y=3√x2 的单调性
y′=2313√x
x=0 是该函数的分界点,因为在此处导数不存在
x<0 时,y′<0,函数单调递减;x>0 时,y′>0,函数单调递增
-
凹凸性的定义
(有没有联想到高中时接触过的极值点偏移类型的题目?)
比较中点函数值与函数值中点的大小:对区间内任意 x1<x2,有
凹:f(x1+x22)<f(x1)+f(x2)2
凸:f(x1+x22)>f(x1)+f(x2)2
-
凹凸性的性质
凹:f′′(x)>0
凸:f′′(x)<0
这一性质通过观察函数图像切线斜率的变化可以很直观的理解;这里还是用拉格朗日中值定理进行证明
对于定义域内的 x1,x2(x1<x2),x0=x1+x22,f′′(x)>0 (证明 f′′(x)>0 函数为凹函数)
在 [x1,x0],f(x0)−f(x1)=f′(ξ1)(x0−x1),ξ1∈(x1,x0)
在 [x0,x2],f(x2)−f(x0)=f′(ξ2)(x2−x0),ξ2∈(x0,x2)
两式相减整理得
2f(x0)−[f(x1)+f(x2)]=12(x2−x1)(f′(ξ1)−f′(ξ2))
对导函数 f′(x) 再次使用一次拉格朗日中值定理
f′(ξ1)−f′(ξ2)=f′′(η)(ξ1−ξ2),η∈(ξ1,ξ2)
由条件可知 f′′(η)>0,x2−x1>0,ξ1−ξ2<0
∴2f(x0)−[f(x1)+f(x2)]=12(x2−x1)(f′(ξ1)−f′(ξ2))=12(x2−x1)f′′(η)(ξ1−ξ2)<0
∴f(x0)<f(x1)+f(x2)2
x
-
拐点
类似研究单调性时的 分界点:函数的 拐点 是指 f′′(x)=0 的点或者二阶导数不存在的点 (这是一个充分不必要条件)
函数在经过拐点后,凹凸性发生改变 (这才是充要条件)
当解答关于分析函数凹凸性的相关题目时,研究函数的二阶导数,先找到函数的拐点,再对各个区间进行分段讨论
x
-
利用函数的凹凸性进行证明
例:求证 ea+eb2>ea+b2,a≠b
对于 f(x)=ex,f′′(x)\=ex>0
∴f(x) 是凹函数,对于任意定义域内的 a,b 都有
f(a)+f(b)2>f(a+b2)
得证
3.4.1 极值
-
极大值(点)与极小值(点)
U(x0),∀x∈U(x∩0) 都有 f(x)<f(x0),那么称 f(x0) 为一个极大值,x0 为一个极大值点
U(x0),∀x∈U(x∩0) 都有 f(x)>f(x0),那么称 f(x0) 为一个极小值,x0 为一个极小值点
极值是一个局部概念,对于某个函数,极值不唯一,也不一定相等
-
极值点 ⇒ 驻点或导数不存在的点 (充分不必要)
f(x) 在 x0 可导,且在 x0 取极值,则 f′(x0)=0 (可导函数的极值点一定是驻点)
证:设在 x0 取极大值,则 ∀x∈U(x∩0) 都有 f(x)<f(x0)
左导数 limΔx→0−f(x0+Δx)−f(x0)Δx≥0
右导数 limΔx→0+f(x0+Δx)−f(x0)Δx≤0
又函数在 x0 可导 ∴ x0 处左右导数相等,f′(x0)=0 得证
-
讨论定理 2 充要的补充条件
f(x) 在 (x0−c,x0+c) 内连续,在 x0 的去心邻域上可导,且 f′(x0)=0 或在 x=x0 时导数不存在
(1)左增右减:x∈(x0−c,x0),f′(x)>0;x∈(x0,x0+c),f′(x)<0 则 x0 为极大值点
(2)左减右增:则 x0 为极大值点
(3)左右均增(减):f′(x) 在 x0 处不变号,x0 不是极值点
运用该结论解答求极值点相关题目:
(1) 在定义域内,找到驻点与导数不存在的点
(2) 判断 f′(x) 在上述点左右的符号 (画 x−f′(x)−f 表, 3.4-32:00)
-
若在 x=x0 处有二阶导, f′(x0)=0,f′′(x0)≠0:若 f′′(x0)>0,则 x0 为极小值点;若 f′′(x0)<0,则 x0 为极大值点
证:当 f′(x0)=0,f′′(x0)>0
f′′(x0)=limΔx→0f′(x0+Δx)−f′(x0)Δx=limΔx→0f′(x0+Δx)Δx>0
∴limΔx→0−f′(x0+Δx)<0,limΔx→0+f′(x0+Δx)>0
左减右增,∴x0 为极大值点得证
注意:当 f′′(x0)=0 时 x0 可能为极值点,也可能不是,此时应采取结论 3 进行解答
3.4.2 最值
-
最小值(点)与最大值(点)
在定义域 I 有定义,x∈I,都有
f(x)≥f(x0) 则 f(x0) 是最小值,x0 是最小值点
f(x)≤f(x0) 则 f(x0) 是最大值,x0 是最大值点
最值是一个全局概念,最值是唯一的
-
求最值点
找到定义域内所有:驻点,导数不存在的点,端点
其中函数值最大的点为最大值点;函数值最小的点为最小值点
-
特殊的最值点
在 I 上连续且单调:最值点一定位于端点
在 I 上有且只有一个极值点:该极值点一定是一个最值点
3.5 函数作图
-
函数的水平渐近线
若 limx→∞f(x)=a,则 y=a 是其的一条水平渐近线 (注意区分是朝正无穷渐进还是朝负无穷渐进)
-
函数的垂直渐近线
若 limx→x0f(x)=∞,则 x=x0 是其的一条垂直渐近线
一般来说,分式函数 f(x)g(x) 有垂直渐近线 x=x0,则有 g(x0)=0
-
函数的斜渐近线
函数在 x 趋于无穷时 y 趋于某条直线 y=kx+b,即 limx→∞f(x)=kx+b,即 y=kx+b 是其的一条斜渐近线
对于 f(x) 的斜渐近线 y=kx+b 有
limx→∞(f(x)−kx)=b
limx→∞f(x)x=limx→∞kx+bx=limx→∞(k+bx)=k
由上式可以看出,一般趋近无穷时表现为一次的函数才具有斜渐近线 (例分母的次数为分子的次数多 1)
-
例:求渐近线的相关题目
求函数 f(x)=x3x2+2x−3 的渐近线
(1)limx→inftyf(x)=∞ 所以无水平渐近线
(2)x2+2x−3=0 ∴x=−3 或 1 所以有两条垂直渐近线 x=−3 与 x=1
(3) limx→∞f(x)x=limx→∞x2x2+2x−3=1,limx→∞(f(x)−x)=−2,所以有一条斜渐近线 y=x−2
-
微分法作图
(1)找到定义域上:不连续点(一般是分母等于 0 的点),与坐标轴相交的点
(2)研究函数的奇偶性,周期性
(3)研究函数的渐近线 (水平,垂直,斜)
(4)研究 f′(x)=0,f′′(x)=0,f′,f′′ 不存在的点,以确定函数的极值点,驻点(增减性),拐点(凹凸性),并作出 f′−f′′−f 表格
(5)其他特殊点
4.1 不定积分
-
定义与符号
在微积分中,一个函数 f 的不定积分,或原函数,是一个导数等于 f 的函数 F,即 F′=f
不定积分符号 ∫:∫f(x)dx=F(x)+c
若 F(x) 是 f(x) 的一个原函数,则我们将 f(x) 的全体原函数 F(x)+c 称为 f(x) 的不定积分
-
一些性质
- [∫f(x)dx]′=f(x)
∫f′(x)dx=f(x)+c (积分和求导可视为互为逆运算)
- ∫kf(x)dx=k∫f(x)dx (k 为常数或与 x 无关的变量)
- ∫[f1(x)+f2(x)+...+fn(x)]dx=∫f1(x)dx+∫f2(x)dx+...+∫fn(x)dx (n必须是有限的)
-
基本积分公式
- ∫0dx=c
- ∫kdx=kx+c
- ∫xadx=1a+1xa+1+c(a≠−1)
- ∫1xdx=ln|x|+c
- ∫exdx=ex+c
- ∫sinxdx=−cosx+c
- ∫cosxdx=sinx+c
- ∫1√1−x2dx=arcsinx+c
- ∫11+x2dx=arctanx+c
- ∫axdx=1lnaax+c
4.2.1 第一换元积分法 (凑微分法)
-
在求不定积分时,把被积分式凑成某个函数的微分的方法称为凑微分法:
其核心是利用公式 dy=f′(x)dx 将微分 d 外面的某项 “拿” 到 d 里面去 (变成原函数) 并凑基本积分公式
∫g(x)dx=∫f(ϕ(x))ϕ′(x)dx=∫f(ϕ(x))dϕ(x)=∫f(u)du=F(u)+c=F(ϕ(x))+c
-
例题

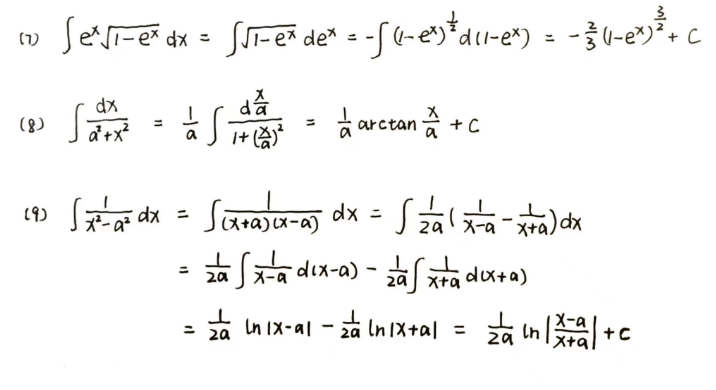

若被积分式的三角函数 (sinx,cosx) 是奇数次,就将其中某一项拿到 d 里去,再运用 sin2x+cos2x=1 转换成统一的三角函数
若本来就是偶数次,则运用倍角公式,和差化积等等公式进行统一
4.2.2 第二换元积分法
-
第二类换元法的基本形式是 f(x),x=g(t),f(x)=f(g(t)),是在被积函数的自变量 x 后面增加一级自变量 t 取代原来的自变量,求出积分之后再回代 x
使用第二类换元法是要改变被积函数形式的,通常用来积分根式、三角函数
∫f(x)dx=∫f(ϕ(t))ϕ′(t)dt,x=ϕ(t)
-
例题

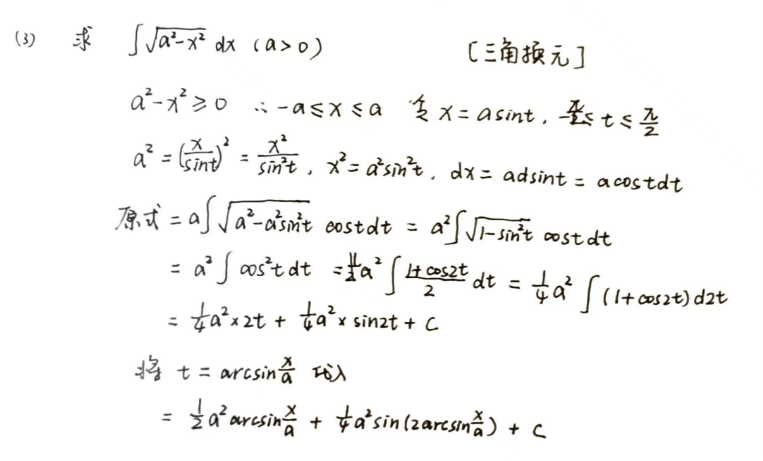
-
一些常见三角换元题型总结的公式
∫dxx2−a2=12aln|x−ax+a|+c
∫dxa2+x2=12arctanxa+c
4.2.3 分部积分法
-
分部积分法推导
对于求导公式 u′v′=u′v+v′u 等式两边同时对 x 求不定积分
∫(u′v′)dx=∫vu′dx+∫uv′dx
∴uv=∫vdu+∫udv,∫udv=uv−∫vdu
-
例题
- ∫xsinxdx=−∫xdcosx=−(xcosx−∫cosxdx)=−xcosx+sinx+c
- ∫xexdx=∫xdex=xex−∫exdx=(x−1)ex+c
- ∫xlnxdx=12∫lnxdx2=12(x2lnx−∫x2dlnx)=12(x2lnx−∫xdx)=12(x2lnx−12x2)+c
- ∫excosxdx=∫exdsinx=exsinx−∫sinxdex=exsinx−∫exsinxdx=exsinx+∫exdcosx=exsinx+excosx−∫cosxdex=exsinx+excosx−∫excosxdx
∴∫excosxdx=exsinx+excosx2+c (多次分部积分+方程思想)
-
反(三角函数)对(数函数)幂(函数/多项式函数)指(数函数)三(角函数),谁靠后谁与 d 结合再使用分部积分法
4.3 有理函数的积分
对形如 P(x)Q(x) 的函数 (P(x),Q(x) 均为多项式) 求积分
-
先将 P(x)Q(x) 转化为真分式 (分母多项式的次数>分子多项式的次数)
若 Q(x) 次数 <P(x) 次数:使用多项式除法(大除法) P(x)Q(x)=a+P1(x)Q(x) ,此时得到真分式 P1(x)Q(x)
若 Q(x) 次数 =P(x) 次数:使用配方法 P(x)Q(x)=aQ(x)−aQ(x)+P(x)Q(x)=a+P(x)−aQ(x)Q(x) (a 取分子分母最高次项系数之比以消去分子的最高次项,以得到真分式)
若 Q(x) 次数 >P(x) 次数:本身就是真分式,无需转化
-
对于转化后形如 ∫1ax2+bx+cdx 的真分式积分
若 b2−4ac=0:则 ∫1ax2+bx+cdx=∫1a(x−x1)2dx=∫1a(x−x1)−2d(x−x1)=−1a(x−x1)−1+c
若 b2−4ac>0:则 ∫1ax2+bx+cdx=∫1a(x−x1)(x−x2)dx=1a∫(Ax−x1+Bx−x2)dx,这一步后使用待定系数法列方程解出 A 与 B,再分别求积分∫Ax−x1d(x−x1)+∫Bx−x2dx−x2=Aln|(x−x1)|+Bln|(x−x2)|+c
若 b2−4ac<0:则 ax2+bx+c=a(x+x1)2+h=h(√ah(x+x1))2+1,采用 ∫11+x2dx=arctanx+c 公式求解
-
对于转化后形如 ∫dx+eax2+bx+cdx 的真分式积分
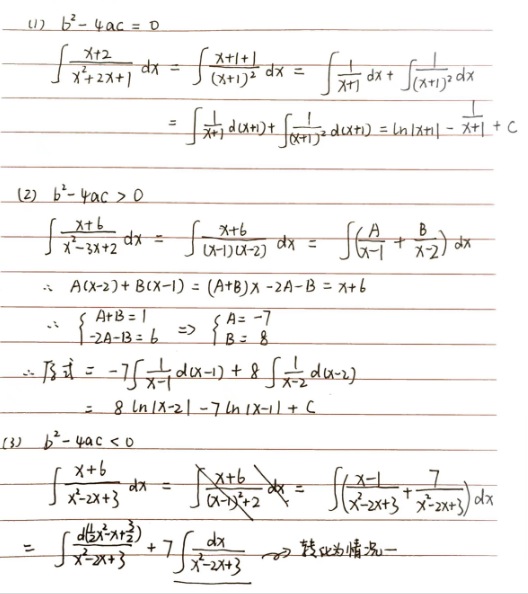
-
其他







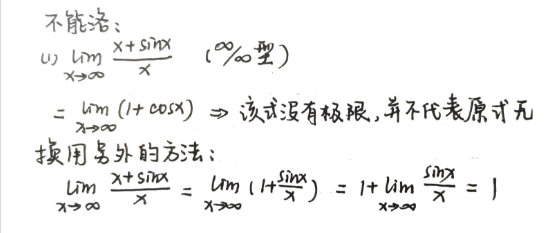
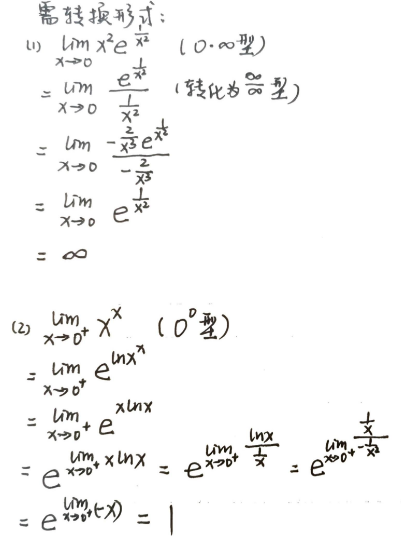

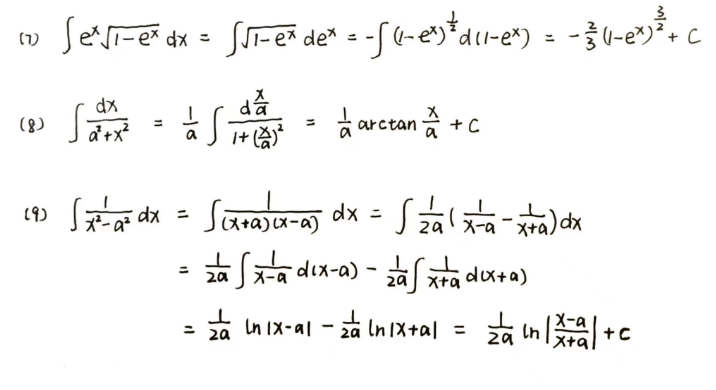


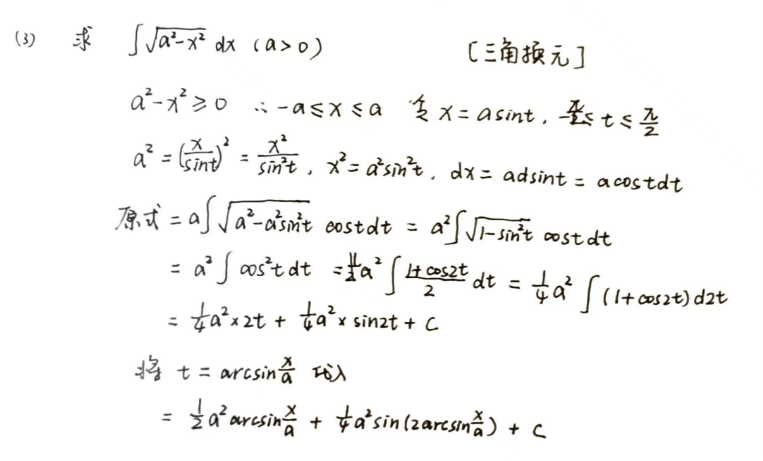
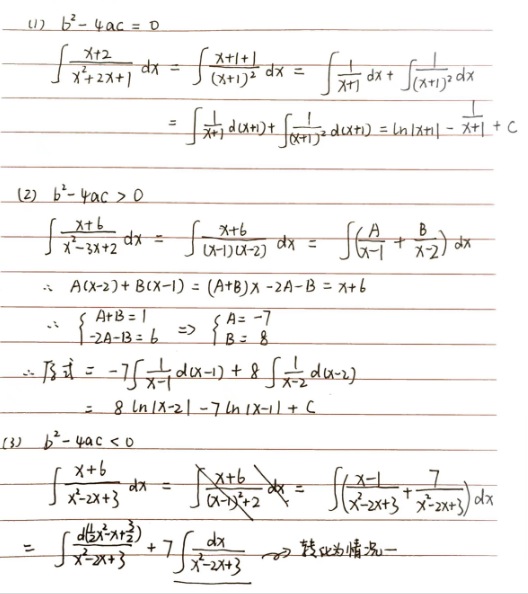






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 【自荐】一款简洁、开源的在线白板工具 Drawnix