NOIP模拟101(多校33)
T1 ladice
解题思路
我们把一个物品看做 \(A_i\) 与 \(B_i\) 之间的连边。
那么如果加入这条边之后联通块中有超过两个环或者两个环就是不合法的,也就是合法的状态只能是一个基环树和树的森林这样一个形态。
直接并茶几判断连通性,标记一下当前的联通块中是否有环就好了。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=3e5+10;
int n,m,fa[N];
bool vis[N];
int find(int x)
{
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
#undef int
int main()
{
#define int register long long
freopen("ladice.in","r",stdin); freopen("ladice.out","w",stdout);
m=read(); n=read();
for(int i=1;i<=n;i++) fa[i]=i;
while(m--)
{
int x,y; x=find(read()); y=find(read());
if(x==y&&vis[x]){printf("SMECE\n");continue;}
if(x!=y&&vis[x]&&vis[y]){printf("SMECE\n");continue;}
if(x==y) vis[x]=true;
else fa[x]=y,vis[y]|=vis[x];
printf("LADICA\n");
}
return 0;
}
T2 card
解题思路
主要是 DP 方程的含义比较难想,\(f_{i,j,k,0/1}\) 表示当前栈中自栈顶到栈底前三个标号是 \(i,j,k\) 。
并且当前可以是否可以选择第一个或者第三个,对于一种已经确定的状态而言,设栈的前三个元素是 \(x,y,z\) ,那么\(z\) 前面的所有牌除了 \(x,y\) 以外一定都已经被取走了,直接前缀和计算即可。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=510,INF=1e18;
int n,ans,pre[N];
bool f[N][N][N][2];
struct Node{int a,b,val;}s[N];
bool judge(int x,int y){return s[x].a==s[y].a||s[x].b==s[y].b;}
#undef int
int main()
{
#define int register long long
freopen("card.in","r",stdin); freopen("card.out","w",stdout);
n=read();
for(int i=1;i<=n;i++)
s[i].a=read(),s[i].b=read(),
s[i].val=read(),pre[i]=pre[i-1]+s[i].val;
f[1][2][3][0]=true; f[1][2][3][1]=true;
f[2][3][4][0]=judge(1,2); f[1][2][4][1]=judge(3,4);
f[1][2][4][0]=judge(1,3); f[2][3][4][1]=judge(1,4);
for(int i=1;i<=n+5;i++)
for(int j=i+1;j<=n+5;j++)
for(int k=j+1;k<=n+5;k++)
{
if(f[i][j][k][0])
{
f[j][k][k+1][0]|=judge(i,j);
f[j][k][k+1][1]|=judge(i,k+1);
ans=max(ans,pre[min(k-1,n)]-s[j].val);
}
if(f[i][j][k][1])
{
f[i][j][k+1][0]|=judge(k,i);
f[i][j][k+1][1]|=judge(k,k+1);
ans=max(ans,pre[min(k,n)]-s[i].val-s[j].val);
}
}
printf("%lld",ans);
return 0;
}
T3 dojave
解题思路
假设当前选中子串的 \(xor\) 和为 \(Sum\) ,设 \(t=2^M-1\) ,\(d=t\otimes Sum\),我们称 \((x,y)\) 配对当且仅当 \(x\otimes y=Sum\otimes t\) 。
先放一下结论:
不合法的序列一定是长度为 4 的倍数并且序列中的元素可以两两进行配对。
首先序列中元素如果不是两两配对的这个序列一定是合法的。
奇数的情况一定合法,因为至少会存在一个在序列中的 \(x\) 在序列外有一个 \(y\) 与之配对。
对于偶数序列元素两两配对的的情况只有 长度为 4 的倍数才是不合法的。
我们以长度为 6 的为例,那么 \(Sum=d\otimes d \otimes d\) 但是显然 \(d\neq Sum\) ,于是这种情况不存在,其他二的倍数可以类推。
然后代码实现的话可以整一个异或前缀和+桶判断,也可以给两个异或为 \(t\) 的附上两个绝对值相同但是符号不同的数做一遍无序 Hash 。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
mt19937 rnd(1ull*time(0)*clock()*rnd()*rand());
const int N=(1<<20)+10;
const ull base=13331; ull t;
int n,m,ans,s[N],pre[N][2],pos[N];
unordered_map<ull,int> cnt[4];
ull id(int x,int y){return 1ull*x*base+y;}
#undef int
int main()
{
#define int long long
freopen("dojave.in","r",stdin); freopen("dojave.out","w",stdout);
m=read(); n=1<<m; ans=n*(n+1)/2;
if(m==1) printf("2"),exit(0); cnt[0].insert(make_pair(0,1));
for(int i=1;i<=n;i++) s[i]=read(),pos[s[i]]=i;
for(int k=0;k<=1;k++) for(int i=1;i<=n;i++) pre[i][k]=pre[pos[(n-1)^s[i]]][k]=rnd()|(rnd()<<15);
for(int k=0;k<=1;k++) for(int i=1;i<=n;i++) pre[i][k]^=pre[i-1][k];
for(int i=1;i<=n;i++) cnt[i%4].insert(make_pair(id(pre[i][0],pre[i][1]),0));
for(int i=1;i<=n;i++) t=id(pre[i][0],pre[i][1]),ans-=cnt[i%4].find(t)->second,cnt[i%4][t]++;
printf("%lld",ans);
return 0;
}
T4 drop
解题思路
求水不是特别好求,我们考虑求出 水+柱子 的体积最后再减去柱子的体积。
发现对于最高的柱子在中间的情况其实可以把最高柱子一侧的柱子平移到另一边,其实是一样的,类似于下图的这种情况:
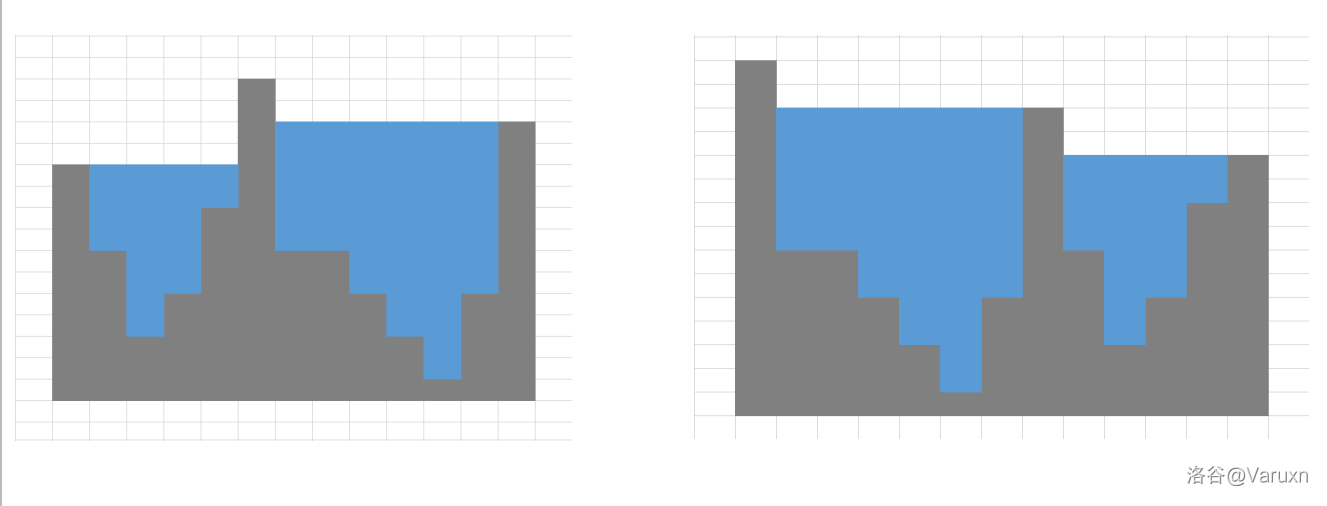
由于我们计算的是 水+柱子 的体积,因此对于一个位置 \(pos\) 它有意义当且仅当它比他左边或者右边的柱子高。
同时根据上图,我们可以发现其实所有柱子和水的体积之和就是两个次高柱子的高度。
那么我们可以先将所有的柱子从小到大枚举,每次插入一个次小值,然后枚举插入这个柱子后可以构成几个 水+柱子 的体积是这样高度的格子。
一个类似于背包的东西直接 bitset 维护。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=5e2+10,M=25e3+10;
int n,cnt,sum,s[N];
bitset<M> bit[N],ans;
#undef int
int main()
{
#define int long long
freopen("drop.in","r",stdin); freopen("drop.out","w",stdout);
n=read(); for(int i=1;i<=n;i++) s[i]=read(),sum+=s[i]; ans[sum]=true;
sort(s+1,s+n+1,greater<int>()); bit[1][s[1]]=true;
for(int i=2;i<=n;i++) bit[i]|=bit[i-1]<<s[2];
for(int i=3;i<=n;i++) if(s[i]!=s[i-1])
{for(int j=i;j<=n;j++) bit[j]|=bit[j-1]<<s[i];ans|=bit[n];}
for(int i=sum;i<=M-10;i++) if(ans[i]) printf("%lld ",i-sum);
return 0;
}

