NOIP模拟99(多校31)
T1 法阵
解题思路
原题3100,张口放 T1(出题人原话)
思维题,合法的情况其实就是上下两个梯形拼起来的样子。
他们的边界都是在 \(i\) 轴上面,但是不能相交。
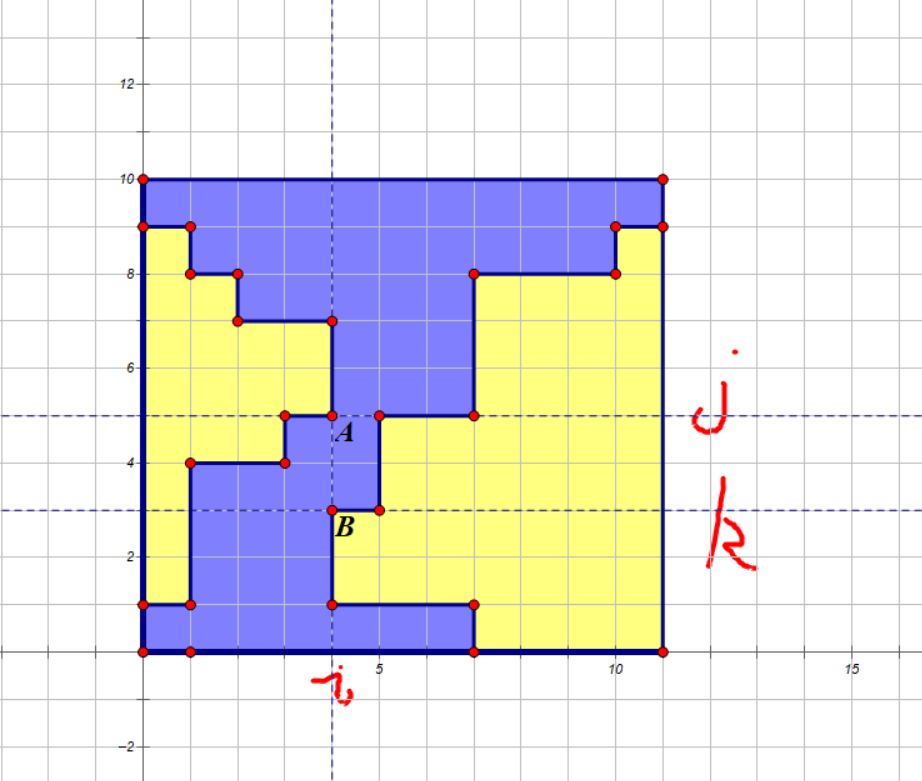
于是我们可以尝试两者相交的纵坐标,再枚举左边梯形的下边界一级右边梯形的上边界,对于答案的话再乘上一个二。
同样的,对于上下两个梯形的情况我们可以把两个边长交换一下再做一遍来实现。
但是有一种情况是重复的,也就是两个颜色都是两个联通块,也就是两个梯形的边界相邻的情况,这个注意一下循环边界问题就好了。
然后再观察一遍这个柿子,它是可以后缀和优化的。。复杂度 \(\mathcal{O}(n^2)\)
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=4e3+100,mod=998244353;
int n,m,ans,fac[N],ifac[N],suf[N];
int power(int x,int y,int p=mod)
{
int temp=1;
for(;y;y>>=1,x=x*x%p)
if(y&1) temp=temp*x%p;
return temp;
}
void init(int lim)
{
fac[0]=ifac[0]=1;
for(int i=1;i<=lim;i++) fac[i]=fac[i-1]*i%mod;
ifac[lim]=power(fac[lim],mod-2);
for(int i=lim-1;i>=1;i--) ifac[i]=ifac[i+1]*(i+1)%mod;
}
void add(int &x,int y){x+=y;if(x>=mod)x-=mod;}
int C(int x,int y){return x<y?0:fac[x]*ifac[y]%mod*ifac[x-y]%mod;}
#undef int
int main()
{
#define int long long
freopen("magic.in","r",stdin); freopen("magic.out","w",stdout);
n=read(); m=read(); init(n+m);
for(int i=1;i<n;i++)
{
for(int k=m;k>=1;k--) suf[k]=(suf[k+1]+C(n-i+m-k,n-i)*C(k+n-i-2,n-i-1))%mod;
for(int j=1;j<m;j++) add(ans,C(i+j-1,i)*C(i+m-j-1,i-1)%mod*suf[j+1]%mod);
}
swap(n,m); memset(suf,0,sizeof(suf));
for(int i=1;i<n;i++)
{
for(int k=m;k>=1;k--) suf[k]=(suf[k+1]+C(n-i+m-k,n-i)*C(k+n-i-2,n-i-1))%mod;
for(int j=1;j<m;j++) add(ans,C(i+j-1,i)*C(i+m-j-1,i-1)%mod*suf[j+2]%mod);
}
printf("%lld",ans*2%mod);
return 0;
}
T2 连通块
解题思路
然而这是个原题,然而我并没有看出来。。。
发现一个点在自身联通块可以到达的最远距离一定是与直径的一端的距离,于是问题就变成了维护直径的两端点。
我们可以把删边操作离线下来改为加边,那么两个联通块合并之后的联通块的直径也一定是来自于之前两个联通块四个直径端点的两两组合。
最后的话直接并茶几判一波连通性即可。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigend long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=2e5+10;
int n,m,tim,dfn[N],siz[N],topp[N],son[N],fa[N],dep[N],ans[N];
int tot=1,head[N],nxt[N<<1],ver[N<<1];
bool vis[N];
pair<int,int> s[N],q[N];
struct Node{int x,y,val;}dis[10];
void add_edge(int x,int y)
{
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void dfs1(int x)
{
siz[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int to=ver[i]; if(siz[to]) continue;
fa[to]=x; dep[to]=dep[x]+1;
dfs1(to); siz[x]+=siz[to];
if(siz[son[x]]<siz[to]) son[x]=to;
}
}
void dfs2(int x,int tp)
{
dfn[x]=++tim; topp[x]=tp;
if(son[x]) dfs2(son[x],tp);
for(int i=head[x];i;i=nxt[i])
if(!dfn[ver[i]])
dfs2(ver[i],ver[i]);
}
int LCA(int x,int y)
{
while(topp[x]^topp[y])
{
if(dep[topp[x]]<dep[topp[y]]) swap(x,y);
x=fa[topp[x]];
}
if(dep[x]>dep[y]) swap(x,y); return x;
}
bool comp(Node x,Node y){return x.val>y.val;}
int dist(int x,int y){return dep[x]+dep[y]-2*dep[LCA(x,y)];}
struct DSU
{
int fa[N];
void init(){for(int i=1;i<=n;i++)fa[i]=s[i].first=s[i].second=i;}
int find(int x)
{
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
if(find(x)==find(y)) return ; x=find(x); y=find(y);
dis[1]=(Node){s[x].first,s[x].second,dist(s[x].first,s[x].second)};
dis[2]=(Node){s[y].first,s[y].second,dist(s[y].first,s[y].second)};
dis[3]=(Node){s[x].first,s[y].second,dist(s[x].first,s[y].second)};
dis[4]=(Node){s[y].first,s[x].second,dist(s[y].first,s[x].second)};
dis[5]=(Node){s[x].first,s[y].first,dist(s[x].first,s[y].first)};
dis[6]=(Node){s[x].second,s[y].second,dist(s[x].second,s[y].second)};
sort(dis+1,dis+7,comp); s[y]={dis[1].x,dis[1].y}; fa[x]=y;
}
}D;
#undef int
int main()
{
#define int long long
freopen("block.in","r",stdin); freopen("block.out","w",stdout);
n=read(); m=read(); D.init();
for(int i=1,x,y;i<n;i++)
x=read(),y=read(),
add_edge(x,y),add_edge(y,x);
dfs1(1); dfs2(1,1);
for(int i=1;i<=m;i++)
{
q[i].first=read(); q[i].second=read();
if(q[i].first==1) vis[q[i].second]=true;
}
for(int i=2;i<=tot;i+=2) if(!vis[i>>1]) D.merge(ver[i],ver[i^1]);
for(int i=m;i>=1;i--)
{
if(q[i].first==1){D.merge(ver[q[i].second<<1],ver[q[i].second<<1|1]);continue;}
pair<int,int> temp=s[D.find(q[i].second)]; int pos=q[i].second;
ans[i]=max(dist(pos,temp.first),dist(pos,temp.second));
}
for(int i=1;i<=m;i++) if(q[i].first==2) printf("%lld\n",ans[i]);
return 0;
}
T3 军队
解题思路
先假设我们可以求出每一行的不同性别的个数,显然每一行可能的贡献只和这一行的数量较小的性别有关系。
并且这个东西是和顺序无关的,那么我们从小到大排序之后的数组假设为 \(s\) 。
那么就一个询问 \((x,y)\) 而言,最优策略一定是选择后 \(x\) 个,对于每一个 \(s_i\) 而言,设 \(t=\min(s_i,\frac{y}{2})\) ,这个位置的贡献就是 \(t\times(y-t)\) 。
我们可以二分出一个边界,对于 \(s_i>\frac{y}{2}\) 的情况直接算就好了,另一种情况的答案就是 \((y-s_i)\times s_i\) 也就是 \(y\times s_i+s_i^2\) 维护两个前缀和就好了。
现在考虑如何求出每个性别的个数,扫描线是毋庸置疑的,发现 k 非常小,于是我们可以维护一个区间内的前 \(k\) 小的值以及对应个数,直接归并合并即可。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigend long long
#define f() cout<<"RP++"<<endl
#define ls x<<1
#define rs x<<1|1
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=3e5+10;
int n,m,t,mn,q,s[N],pre[N],pre2[N];
vector< pair<int,int> > v[N];
pair<int,int> temp[N<<1];
struct Segment_Tree
{
int laz[N<<2];
vector< pair<int,int> > tre[N<<2];
inline void push_up(int x)
{
int cnt=0,pos=0; tre[x].clear();
for(auto it:tre[ls])
{
while(pos<=tre[rs].size()-1&&tre[rs][pos].first<=it.first)
temp[++cnt]=tre[rs][pos++];
temp[++cnt]=it;
}
while(pos<=tre[rs].size()-1) temp[++cnt]=tre[rs][pos++];
for(int i=1;i<=cnt;i++)
{
pair<int,int> it=temp[i];
if(!tre[x].size()){tre[x].push_back(it);continue;}
if(tre[x][tre[x].size()-1].first==it.first) tre[x][tre[x].size()-1].second+=it.second;
else tre[x].push_back(it);
}
while(tre[x].size()>mn) tre[x].pop_back();
}
void push_down(int x)
{
for(int i=0;i<(int)tre[ls].size();i++) tre[ls][i].first+=laz[x];
for(int i=0;i<(int)tre[rs].size();i++) tre[rs][i].first+=laz[x];
laz[ls]+=laz[x]; laz[rs]+=laz[x]; laz[x]=0;
}
void build(int x,int l,int r)
{
if(l==r) return tre[x].push_back({0,1}),void();
int mid=(l+r)>>1; build(ls,l,mid); build(rs,mid+1,r); push_up(x);
}
void insert(int x,int l,int r,int L,int R,int val)
{
if(L<=l&&r<=R)
{
for(int i=0;i<(int)tre[x].size();i++) tre[x][i].first+=val;
laz[x]+=val; return ;
}
int mid=(l+r)>>1; if(laz[x]) push_down(x);
if(L<=mid) insert(ls,l,mid,L,R,val);
if(R>mid) insert(rs,mid+1,r,L,R,val);
push_up(x);
}
}T;
#undef int
int main()
{
#define int register long long
freopen("army.in","r",stdin); freopen("army.out","w",stdout);
n=read(); m=read(); t=read(); mn=read(); q=read(); T.build(1,1,m);
for(int i=1,x,y,x2,y2;i<=t;i++)
x=read(),y=read(),x2=read(),y2=read(),
v[x].push_back({y,y2}),v[x2+1].push_back({-y,y2});
for(int i=1;i<=n;i++)
{
for(auto it:v[i]) T.insert(1,1,m,abs(it.first),it.second,it.first<0?-1:1);
int cnt=0;
for(auto it:T.tre[1])
if(it.first<mn) cnt+=it.second;
else break;
s[i]=min(cnt,m-cnt);
}
sort(s+1,s+n+1);
for(int i=1;i<=n;i++) pre[i]=pre[i-1]+s[i],pre2[i]=pre2[i-1]+s[i]*s[i];
while(q--)
{
int x,y,pos; x=read(); y=read();
pos=lower_bound(s+1,s+n+1,y/2)-s;
if(n-pos+1>=x){printf("%lld\n",x*(y/2)*(y-y/2));continue;}
printf("%lld\n",(n-pos+1)*(y/2)*(y-y/2)+y*(pre[pos-1]-pre[n-x])-(pre2[pos-1]-pre2[n-x]));
}
return 0;
}
T4 棋盘
解题思路
用两个栈维护队列的情况。
发现转移是一个矩阵,记录从 \(i\rightarrow j\) 的方案数
那么我们维护两个栈,每个维护一段区间\([head,mid],[mid+1,tail]\)。
第一个栈的第 \(i\) 个元素,维护从第 \(i\) 行到第 \(mid\) 行的转移
第二个栈的元素维护从 \(mid\) 到 \(j\) 的转移。
插入操作直接在第二个栈加入一个元素,删除操作需要分类讨论第一个栈的情况,询问直接将两个栈合并即可。
由于是马步,所以需要维护 \(i\rightarrow mid+1,mid+1\rightarrow j\) 的转移。。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+10,M=25,mod=998244353;
int q,n,head=1,tail,mid,f[N][M][M],g[N][M][M];
char ch[M];
bool s[N][M];
void add(int &x,int y){x+=y;if(x>=mod)x-=mod;}
void work(int now,int pre1,int pre2,int dp[][M][M])
{
memset(dp[now],0,sizeof(dp[now]));
for(int i=1;i<=n;i++) if(!s[now][i])
for(int j=1;j<=n;j++)
{
if(i>2) add(dp[now][i][j],dp[pre1][i-2][j]);
if(i>1) add(dp[now][i][j],dp[pre2][i-1][j]);
if(i+2<=n) add(dp[now][i][j],dp[pre1][i+2][j]);
if(i+1<=n) add(dp[now][i][j],dp[pre2][i+1][j]);
}
}
void Rebuild()
{
mid=tail; memset(f[tail],0,sizeof(f[tail]));
for(int i=1;i<=n;i++) f[tail][i][i]=s[tail][i]^1;
for(int i=tail-1;i>=head;i--) work(i,i+1,i+2>tail?0:i+2,f);
if(head==tail) return ; memset(g[tail-1],0,sizeof(g[tail-1]));
for(int i=1;i<=n;i++) g[tail-1][i][i]=s[tail-1][i]^1;
for(int i=tail-2;i>=head;i--) work(i,i+1,i+2>=tail?0:i+2,g);
}
void Insert()
{
scanf("%s",ch+1); tail++;
for(int i=1;i<=n;i++) s[tail][i]=ch[i]=='#';
if(head<=tail&&head>mid) return Rebuild();
work(tail,tail-1,tail-2<mid?0:tail-2,f);
if(tail!=mid+1) return work(tail,tail-1,tail-2<=mid?0:tail-2,g),void();
for(int i=1;i<=n;i++) g[tail][i][i]=s[tail][i]^1;
}
void Delete(){head++;if(head<=tail&&head>mid)Rebuild();}
void Solve()
{
int ans=0,x,y; x=read(); y=read();
if((head==tail&&x!=y)||head>tail||s[head][x]||s[tail][y]) return printf("0\n"),void();
if(head==tail) return printf("1\n"),void();
for(int i=1;i<=n;i++) add(ans,f[head][x][i]*f[tail][y][i]%mod);
if(tail<=mid||head>=mid) return printf("%lld\n",ans),void();
for(int i=1;i<=n;i++)
{
if(i>1) add(ans,g[head][x][i]*g[tail][y][i-1]%mod);
if(i<n) add(ans,g[head][x][i]*g[tail][y][i+1]%mod);
}
printf("%lld\n",ans);
}
#undef int
int main()
{
#define int long long
freopen("chess.in","r",stdin); freopen("chess.out","w",stdout);
n=read(); q=read();
while(q--)
{
scanf("%s",ch+1);
if(ch[1]=='A') Insert();
else if(ch[1]=='D') Delete();
else Solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号