11.15杂题选做
P3298 [SDOI2013]泉
本来是一个可以一遍切的题。然而数组开小就。。。。
发现 \(N\) 不是特别大,并且泉水只有 6 种,于是我们可以暴力枚举每一种选择情况,然后统计相同的个数计入答案。
发现会算重复,重复的部分直接二项式反演解决掉。200紫题祭 (code)
P4211 [LNOI2014]LCA
树链剖分+线段树或者树状数组。。
对于每一个询问而言,一个结点的贡献其实就是子树内在 \([l,r]\) 这个区间中的节点数,这个东西直接树链剖分。
发现对于每个询问都搞一次的话复杂度不如暴力,再观察一下,我们维护的其实是一个类似于前缀性质的东西。
于是直接将一个区间拆分成两个区间贡献相减的形式。。不得不说树链剖分和树状数组常数实在是小(code)
CF297E Mystic Carvings
题目藐视不太清楚,大概就是从若干个边中选择三条,在这三条边的两个端点分别建立熊洞,定义两点之间的距离为经过顺着圆或者无向边经过的熊洞数量减一,假设选出的三条边是 \((a,b),(c,f),(e,f)\) 我们要使得 \(dis(a,b)=dis(c,f)=dis(e,f)\) ,求方案数。
发现三条弦的状态只有五种:

并且满足条件的只有第二个第五个,但是不是特别好算,我们可以算 1,3,4 的,然后用总方案数 \(\binom{n}{3}\) 减去就好了。
设 \(l_i,r_i\) 分别表示左右两侧的与第 \(i\) 条弦不相交的弦的数量。
情况 1 的方案就是 \(\sum\limits_{i=1}^n l_i\times r_i\) 。
情况 3,4 我们把它们放在一起计算。发现这两张图的共同点是:
三条弦中有两条满足另外的两条弦一条与其相交,一条与其相离。
同时需要注意每一组有两条弦满足情况因此方案数就是:
剩下问题就是对于 \(l,r\) 数组的计算了, \((x',y')\) 在 \((x,y)\) 左边并且不相交只会满足下面三个条件之一:
-
\(x'<x并且y'<x\)
-
\(x'<x并且y'>y\)
-
\(x'>y并且y'>y\)
对于 \((x',y')\) 在 \((x,y)\) 右边并且不相交的情况就是 $x'>x并且y'<y $ 。
直接二维偏序解决即可 (code)
AT2389 [AGC016E] Poor Turkeys
一道NOIP模拟23这种远古时代的题目了。
\(f_{i,j}\) 表示如果让 \(i\) 存活 \(j\) 必须从活着的状态到死去的状态。
我们逆推,对于当前扫到的火鸡 \(i\) 以及一对不可能同时存活的火鸡 \((x,y)\) 如果此前 \(i\) 的存活已经需要两者来死亡了,因为我们是逆推,先执行这个操作,那么 \(i\) 一定不会活着的。。
同样的对于 \(x,y\) 对于 \(i\) 是否需要死亡的状态也就可以转移了。
那么最后答案就是两只鸡的 \(f\) 没有交集。 bitset 实现 (code)
AT2673 [AGC018D] Tree and Hamilton Path
哈密顿路不是特别好求,我们尝试着求一下最长哈密顿回路再减去一个最短的路径。
假设一条边所连接的两个联通块大小较小值是 \(siz\) 那么大小较小的这一棵子树中的点都会经过这条边,毕竟我们要求最长的哈密顿回路,盗个图:
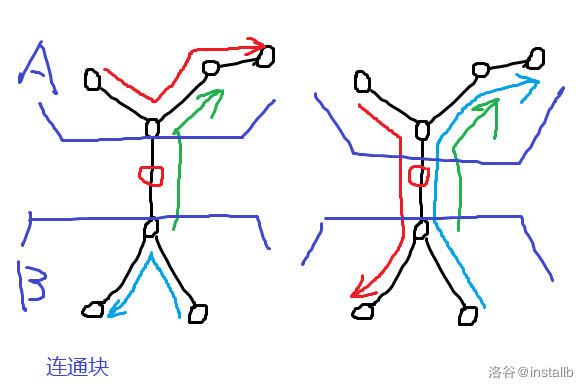
然后就是如何去除那一条多余的路径了,然而随便选择一条路径是不对的,因为他不一定在我们的最优的哈密顿回路中。
最优解的路径一定经过重心。
因为重心保证了它的所有子树的大小都小于或者等于 \(\frac{n}{2}\) 。
我们可以做到每一条路径,都是在重心的两个不同子树中各取一点相连,再盗一个图:
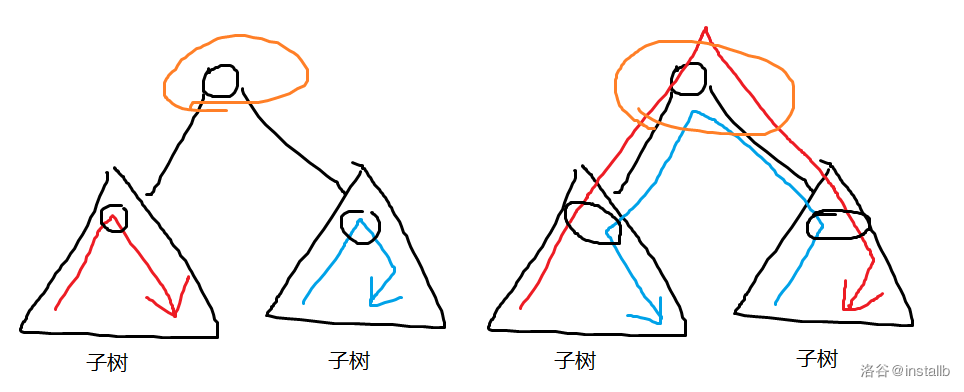
对于只有一个重心的情况就直接选择与重心相连的最短的边删掉,对于有两个重心的情况直接删去他们之间的边就好了。 (code)
AT2705 [AGC019F] Yes or No
假设 \(N\ge M\) 显然我们至少会猜对 \(N\) 个答案。
把问题抽象到一个二维平面上面,横纵坐标分别为还有多少个 Yes 或者 No 没有出现。
那么每一种答案序列都可以看作是一个以 \((N,M)\) 为起点只可以向下或者向左走的序列,总方案就是 \(\binom{N+M}{N}\)
我们的问题件就变成了对于经过 \(y=x\) 这条线的答案序列我们蒙对答案的概率。
显然答案是 Yes 或者 No 是等价的,那么对于一个点 \((i,i)\) 而言,经过它的方案数就是 \(\binom{2\times i}{i}\times\binom{n+m-2\times i}{n-i}\) 。
最后再除以一个总方案数就好了 (code)
AT3857 [AGC020C] Median Sum
只能说代码实现难度为 0 。
bitset 实现一个背包,假设物品总和是 \(cnt\) 对于任意的一个可以构成的 \(x\) , \(cnt-x\) 也一定是存在的,直接从 \(\dfrac{cnt}{2}\) 扫就好了。(code)
AT2363 [AGC012C] Tautonym Puzzle
构造题。
我们可以把序列分成两部分,先在后面插入 \(1\sim cnt\) 的升序排列,然后尝试在前面构建一个 \(1\sim n\) 的排列。
那么题目所要求的东西就变成了前半个序列的上升子序列的个数。
考虑从小到大填数,在前面填一个数的贡献是 \(+1\) 在后面加一个数的贡献是 \(\times 2\) 直接递归处理即可 (code)
CF383C Propagating tree
树链剖分大板,直接对于深度的奇数或者偶数开两个树状数组维护,分别给不同的符号就好了。 (code)
P4514 上帝造题的七分钟
二维树状数组维护区间加,区间求和。。
也是维护一个差分数组,操作类似于一维上的情况,需要维护常数项 , x 项, y 项,以及 xy 项。(code)

