NOIP模拟80
学考+OJ改名祭
T1 邻面合并
解题思路
状压 DP 。。。(于是贪心竟然有 60pts 的高分?? code)
状态设计的就非常妙了,如果状态是 1 就表示是一个分割点也就是一个矩形的右边界。
那么对于一个合法的状态需要满足:原矩阵中是 0 的不可以是分割点,并且对于原矩阵中的 1,而言如果不是分割点那么它到前面最近的分割点之间就不可以有 0 。
然后考虑对于不同的状态进行合并,如果上一行的这个位置不是分割点而这一行是显然就需要新开一个矩形。
同样的道理,如果两个矩形的分割点一样但是长度不同也需要新建一个矩形。
code
#include <bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Failed"
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=110,M=20,INF=1e18;
int n,m,ans=INF,f[N][1<<8],adv[N][M][1<<8];
bool s[N][M];
bool check(int pos,int sta)
{
bool can=false;
for(int i=1;i<=m;i++)
{
if(((sta>>i-1)&1)&&!s[pos][i]) return false;
if((sta>>i-1)&1) can=true;
if(!s[pos][i]) can=false;
if(!can&&s[pos][i]) return false;
}
return true;
}
int work(int x,int y,int sta){int pos=y;while(s[x][pos+1]&&(((sta>>pos)&1)^1)) pos++;return pos;}
signed main()
{
freopen("merging.in","r",stdin); freopen("merging.out","w",stdout);
n=read(); m=read(); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) s[i][j]=read();
memset(f,0x3f,sizeof(f)); fill(f[0]+0,f[0]+(1<<m),0);
for(int i=0;i<=n;i++)for(int j=0;j<(1<<m);j++)if(check(i,j))for(int k=1;k<=m;k++)if((j>>k-1)&1)adv[i][k][j]=work(i,k,j);
for(int i=0;i<n;i++)
for(int j=0;j<(1<<m);j++)
{
if(!check(i,j)) continue;
for(int k=0;k<(1<<m);k++)
{
int sum=0; if(!check(i+1,k)) continue;
for(int p=1;p<=m;p++) sum+=(((j>>p-1)&1)^1)&((k>>p-1)&1);
for(int p=1;p<=m;p++) if(((j>>p-1)&1)&&((k>>p-1)&1)) sum+=adv[i][p][j]!=adv[i+1][p][k];
f[i+1][k]=min(f[i+1][k],f[i][j]+sum);
}
}
for(int i=0;i<(1<<m);i++) ans=min(ans,f[n][i]);
printf("%lld",ans);
return 0;
}
T2 光线追踪
解题思路
发现一个矩形有用的部分其实就是左边以及下面的两条边。
正如官方题解所说,可以现将斜率或者到 x 轴的角度给离散化下来,然后对于对应的进行区间覆盖。
对于平行于 x 轴和平行于 y 轴的方向开两颗线段树进行维护。
以平行于 x 的为例,我们维护一个区间最小的纵坐标以及对应的编号。

然后就是对于两颗线段树计算的信心进行合并了。
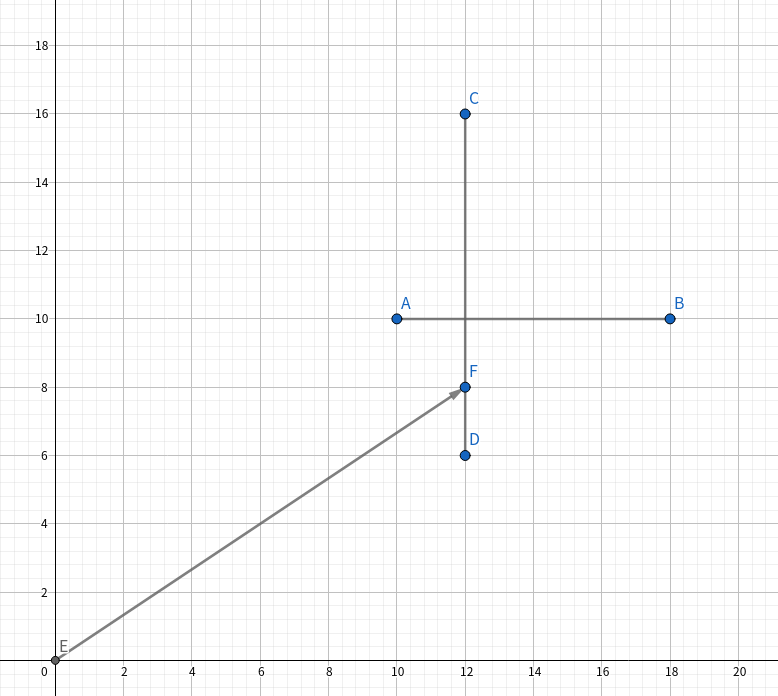
以上图为例(假设维护平行于 x 轴的线段树是 T1,平行于 y 轴的线段树是 T2),那么 T1 的结果是 AB , T2 的结果是 CD 。
显然对于询问 EF 而言答案应该是 CD 。
可以发现以 EF 与 CD 交点的横纵坐标是可以算出来的(其实就是一个一次函数上的某个点)
将交点的纵坐标与 AB 的纵坐标相比较就好。
最后不要忘了特判一下询问的横坐标或者纵坐标是 0 的情况。
code
#include <bits/stdc++.h>
#define ls x<<1
#define rs x<<1|1
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=3e5+10,INF=1e18;
int q,tim,cnt;
double lsh[N];
struct node{int opt,x,y,x2,y2;}s[N];
struct Node
{
int dat,id;
inline Node friend operator + (Node x,Node y)
{
Node z; z.dat=min(x.dat,y.dat);
if(x.dat==y.dat) z.id=max(x.id,y.id);
else if(x.dat<y.dat) z=x;
else z=y; return z;
}
};
struct Segment_Tree
{
Node tre[N<<2],laz[N<<2];
#define push_up(x) tre[x]=tre[ls]+tre[rs];
inline void push_down(int x)
{
tre[ls]=tre[ls]+laz[x]; tre[rs]=tre[rs]+laz[x];
laz[ls]=laz[ls]+laz[x]; laz[rs]=laz[rs]+laz[x];
laz[x].dat=INF; laz[x].id=-1;
}
inline void build(int x,int l,int r)
{
tre[x].dat=INF; tre[x].id=-1; laz[x].dat=INF; laz[x].id=-1;
if(l==r) return ; int mid=(l+r)>>1;
build(ls,l,mid); build(rs,mid+1,r);
}
inline void insert(int x,int l,int r,int L,int R,Node val)
{
if(L<=l&&r<=R) return tre[x]=tre[x]+val,laz[x]=laz[x]+val,void();
int mid=(l+r)>>1; if(~laz[x].id) push_down(x);
if(L<=mid) insert(ls,l,mid,L,R,val);
if(R>mid) insert(rs,mid+1,r,L,R,val);
push_up(x);
}
inline int query(int x,int l,int r,int pos)
{
if(l==r) return tre[x].id;
int mid=(l+r)>>1; push_down(x);
if(pos<=mid) return query(ls,l,mid,pos);
return query(rs,mid+1,r,pos);
}
}T1,T2;
inline double get(int x,int y){return (!x)?INF:(1.0*y)/(1.0*x);}
inline void insert(node temp,int id)
{
int x=temp.x,y=temp.y,x2=temp.x2,y2=temp.y2;
double a=get(x,y2),b=get(x,y),c=get(x2,y);
int pos1=lower_bound(lsh+1,lsh+cnt+1,a)-lsh;
int pos2=lower_bound(lsh+1,lsh+cnt+1,b)-lsh;
int pos3=lower_bound(lsh+1,lsh+cnt+1,c)-lsh;
T1.insert(1,1,cnt,pos2,pos1,(Node){x,id});
T2.insert(1,1,cnt,pos3,pos2,(Node){y,id});
}
signed main()
{
freopen("raytracing.in","r",stdin); freopen("raytracing.out","w",stdout);
q=read();
for(int i=1;i<=q;i++)
{
int opt,x,y,x2,y2; opt=read(); x=read(); y=read(); lsh[++cnt]=get(x,y);
if(opt==1) x2=read(),y2=read(),lsh[++cnt]=get(x2,y),lsh[++cnt]=get(x,y2);
s[i]=(node){opt,x,y,x2,y2};
}
sort(lsh+1,lsh+cnt+1); cnt=unique(lsh+1,lsh+cnt+1)-lsh-1;
T1.build(1,1,cnt); T2.build(1,1,cnt);
int all=0;
for(int i=1;i<=q;i++)
{
if(s[i].opt==1){insert(s[i],i);continue;}
double k=get(s[i].x,s[i].y); all++;
int pos=lower_bound(lsh+1,lsh+cnt+1,k)-lsh;
int pos1=T1.query(1,1,cnt,pos),pos2=T2.query(1,1,cnt,pos);
if(pos1==-1&&pos2==-1){printf("0\n");continue;}
if(pos1==pos2||pos1==-1||pos2==-1){printf("%d\n",max(pos1,pos2));continue;}
double x=s[pos1].x,y=s[pos1].y,x2=s[pos2].x,y2=s[pos2].y;
if(!s[i].y){printf("%d\n",pos1);continue;}
if(!s[i].x){printf("%d\n",pos2);continue;}
if(s[i].y*x<y2*s[i].x){printf("%d\n",pos1);continue;}
if(y2*s[i].x<s[i].y*x){printf("%d\n",pos2);continue;}
printf("%d\n",max(pos1,pos2));
}
return 0;
}
T3 百鸽笼
解题思路
DP ,对于每一个格子分别进行求解。
做一个类似于背包的 DP ,维护当前到了那一位,已经放了多少个鸽笼。
最后容斥一下
code
#include <bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Failed"
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=40,mod=998244353;
int n,s[N],f[N][N*N],c[N*N][N*N];
int rec[N];
int power(int x,int y,int p=mod)
{
int temp=1;
while(y)
{
if(y&1) temp=temp*x%mod;
x=x*x%mod; y>>=1;
}
return temp;
}
void Binom_Work()
{
c[0][0]=1;
for(int i=1;i<=n*30;i++)
{
c[i][0]=1;
for(int j=1;j<=n*30;j++)
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
void solve(int pos)
{
if(rec[s[pos]]) return printf("%lld ",rec[s[pos]]),void();
memset(f,0,sizeof(f)); int ans=f[0][0]=1,cnt=0;
for(int i=1;i<=n;i++)
if(i!=pos)
{
for(int j=i;~j;j--)
for(int k=cnt;~k;k--)
if(f[j][k])
for(int sum=0;sum<s[i];sum++)
f[j+1][k+sum]=(f[j+1][k+sum]+f[j][k]*c[k+sum][k])%mod;
cnt+=s[i]-1;
}
for(int i=1;i<=n-1;i++)
for(int j=0;j<=cnt;j++)
if(i&1) ans=(ans-f[i][j]*c[j+s[pos]-1][j]%mod*power(power(i+1,mod-2),j+s[pos])%mod+mod)%mod;
else ans=(ans+f[i][j]*c[j+s[pos]-1][j]%mod*power(power(i+1,mod-2),j+s[pos]))%mod;
return printf("%lld ",rec[s[pos]]=ans),void();
}
signed main()
{
freopen("c.in","r",stdin); freopen("c.out","w",stdout);
n=read(); Binom_Work();
for(int i=1;i<=n;i++) s[i]=read();
for(int i=1;i<=n;i++) solve(i);
return 0;
}
T4 滑稽树下你和我
解题思路
二分答案。
发现线段和线段之间的距离可以看做其中一条线段的两个端点到另一条线段的距离。
每次二分出来一个值,用 BFS 判断是否符合条件,BFS 每次存储一个点一条边(也就是 x 所在的节点和 y 所在的边 或者 y 所在的节点和 x 所在的边)
然后每次枚举是点走或者是边走。
对于 一个点到一条线段之间的位置关系分为两种情况:
-
点向线段做垂线垂足落在线段外,这个直接取点到线段两个端点的距离进行比较就好了。
-
点向线段做垂线垂足落在线段内,可以海伦公式或者等面积法,当然如果等面积的话也就是点于线段形成的三角形。
对于我代码中的求法用等底等高就可以轻松的解释。。
code
#include <bits/stdc++.h>
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=2e3+10;
const double eps=1e-7;
double ans;
int n,sx,sy,all,du[N],vis[N][N],a[N],b[N];
int tot=1,head[N],nxt[N<<1],ver[N<<1];
struct Node{double x,y;}s[N];
inline void add_edge(int x,int y)
{
ver[++tot]=y; du[y]++;
nxt[tot]=head[x]; head[x]=tot;
}
inline double dist(Node i,Node j){return sqrt((i.x-j.x)*(i.x-j.x)+(i.y-j.y)*(i.y-j.y));}
inline double dist(Node i,Node j,Node k)
{
bool can1=(k.x-j.x)*(i.x-j.x)+(k.y-j.y)*(i.y-j.y)>0;
bool can2=(j.x-k.x)*(i.x-k.x)+(j.y-k.y)*(i.y-k.y)>0;
if(!can1||!can2) return min(dist(i,j),dist(i,k));
return abs((j.x-i.x)*(i.y-k.y)+(j.y-i.y)*(k.x-i.x))/dist(j,k);
}
queue<pair<int,int> > q[N];
inline void insert(int x,int y,double lim)
{
if(vis[x][y]==all||dist(s[x],s[a[y]],s[b[y]])>lim) return ;
vis[x][y]=all; q[all].push(make_pair(x,y));
}
inline bool check(double lim)
{
all++; while(!q[all].empty()) q[all].pop();
for(int i=head[sx];i;i=nxt[i]) insert(sy,i>>1,lim);
for(int i=head[sy];i;i=nxt[i]) insert(sx,i>>1,lim);
while(!q[all].empty())
{
int x=q[all].front().first,y=q[all].front().second; q[all].pop();
if(du[x]==1&&du[a[y]]==1&&dist(s[x],s[a[y]])<=lim) return true;
if(du[x]==1&&du[b[y]]==1&&dist(s[x],s[b[y]])<=lim) return true;
for(int i=head[x];i;i=nxt[i])
insert(ver[i],y,lim),insert(a[y],i>>1,lim),insert(b[y],i>>1,lim);
}
return false;
}
signed main()
{
freopen("tree.in","r",stdin); freopen("tree.out","w",stdout);
n=read(); sx=read(); sy=read();
for(int i=1,x,y;i<=n;i++) x=read(),y=read(),s[i]=(Node){1.0*x,1.0*y};
for(int i=1,x,y;i<n;i++) x=read(),y=read(),add_edge(x,y),add_edge(y,x),a[i]=x,b[i]=y;
double l=ans=dist(s[sx],s[sy]),r=15e5;
while(r-l>eps)
{
double mid=(l+r)/2.0;
if(check(mid)) r=mid,ans=mid;
else l=mid;
}
printf("%.7lf",ans);
return 0;
}

 「邻面合并·光线追踪·百鸽笼·滑稽树下你和我」on 10.18
「邻面合并·光线追踪·百鸽笼·滑稽树下你和我」on 10.18

 浙公网安备 33010602011771号
浙公网安备 33010602011771号