NOIP模拟49
虚伪的眼泪,会伤害别人,虚伪的笑容,会伤害自己。
前言
暑假集训过后的第一次考试,成绩一般,没啥好说的
T1 Reverse
解题思路
看到这个题的第一眼就感觉是最短路,毕竟题目的样子就好像之前做过的星空的部分。
然后就是在不到十分钟之后机房就充满了敲键盘的声音。
然后就有了几乎是签到的 57pts ,至于思路嘛,只能说是显然。
考完之后有小常数强者直接 \(\mathcal{O(nk)}\) 切掉。
我看了看我在本机上最大的 \(10^5\) 的样例只跑了 \(0.009s\) 的程序,又试了一边考场上造出来的最大数据 \(10s\) 。
一个邪恶的念头在我内心产生了,把 Dijkstra 改成 SPFA ,再配上一个手写队列,最最重要的是一个 卡时 ,于是我们愉快地切掉此题(成功压进 20 行)。
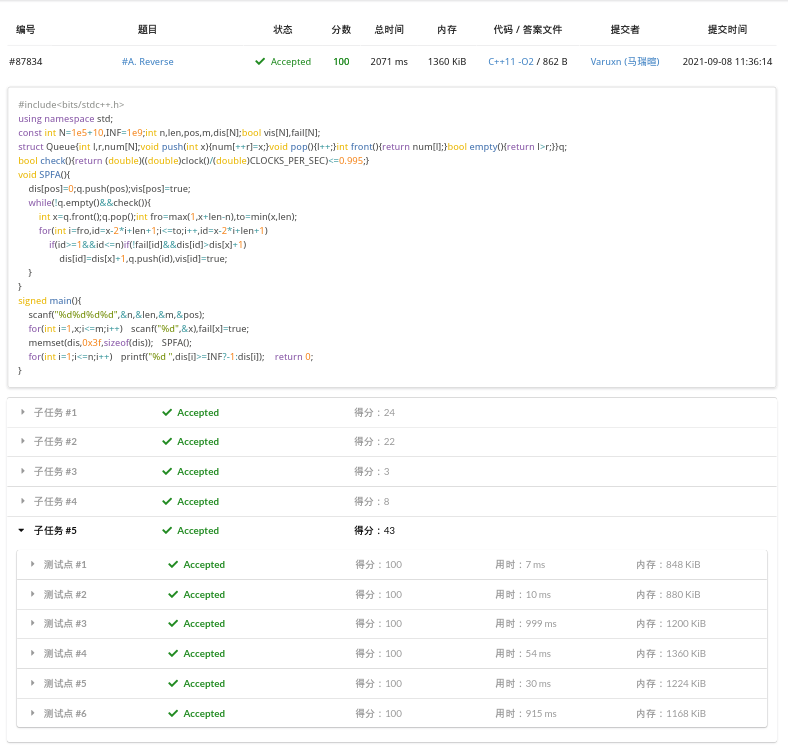
后来又卡了一下,发现好像可以把卡时的东西稍微开大一点,但是手写队列确实是需要。。
还是稍微写一下正解吧,复杂度是 \(\mathcal{O(nlogn)}\),但是链表实现可以达到 \(\mathcal{O(n)}\) 。
我们当然是学习比较快的打法了。。
其实比较简单,发现对于同一个位置的 1 翻转可以到达的位置只可能是奇数或者偶数的一种。
然后可以卡一下范围,类似于翻转的串的左右端点一定在 \([1,n]\) 。
接下来就是可以通过加减操作得到可以到达的区间内的第一个以及最末尾的数字,从链表跳就好了。
对于更新的区间内的链表值于当前区间右端点取 \(\max\) 这样就可以达到每个点只被扫一边的目的了。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Failed"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+10,INF=1e9;
int n,pos,m,len,dis[N],nxt[N];
struct Queue
{
int l,r,num[N];
void push(int x){num[++r]=x;}
void pop(){l++;}
int front(){return num[l];}
bool empty(){return l>r;}
}q;
signed main()
{
n=read(); len=read(); m=read(); pos=read();
memset(dis,0x3f,sizeof(dis)); dis[pos]=0; q.push(pos);
for(int i=1,x;i<=m;i++) x=read(),dis[x]=-1;
for(int i=1;i<=n;i++) nxt[i]=i+2;
while(!q.empty())
{
int x=q.front(); q.pop();
int fro=2*max(1ll,x-len+1)+len-x-1,to=2*min(n-len+1,x)+len-x-1;
for(int i=fro;i<=to;i=nxt[i]) if(dis[i]>dis[x]+1) dis[i]=dis[x]+1,q.push(i);
for(int i=fro,pre=nxt[i];i<=to;i=pre,pre=nxt[i]) nxt[i]=max(nxt[i],to);
}
for(int i=1;i<=n;i++) printf("%lld ",dis[i]>=INF?-1:dis[i]);
return 0;
}
T2 Silhouette
解题思路
二项式反演
不难发现两个数组的顺序对于答案是没有影响的,因此我们可以将它们从大到小进行排序。
那么我们就可以发现,对于所有 \(S=\min(A_i,b_j)\) 相同的位置,从大到小进行枚举。
我们每次所要求的值的范围就变成了一个矩形或者一个 L 形。
先说一下矩形的操作,设 \(f(i)\) 表示至少有 i 行不满足条件的方案数,前提是所有的列都符合条件,假设当前计算的是一个 \(a\times b\) 的矩形,那么根据二项式反演,答案就是 \(\sum\limits_{i=0}^a(-1)^i\times f(i)\)。
同样的假设我们现在求的 L 形是一个 \(A\times B\) 挖去一个 \((A-a)\times(B-b)\) 的形状,我们可以把 L 形看作为两个矩形,也就可以得出下面的柿子:
code
#include<bits/stdc++.h>
#define int long long
#define f() cout<<"Failed"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+10,mod=1e9+7;
int n,ans=1,pos1=1,pos2=1,fac[N],inv[N],fro[N],nex[N];
int power(int x,int y)
{
int temp=1; x%=mod; y%=(mod-1);
while(y)
{
if(y&1) temp=temp*x%mod;
x=x*x%mod; y>>=1;
}
return temp;
}
void init()
{
fac[0]=inv[0]=1; for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;
inv[n]=power(fac[n],mod-2); for(int i=n-1;i>=1;i--) inv[i]=inv[i+1]*(i+1)%mod;
}
int C(int x,int y){return fac[x]*inv[y]%mod*inv[x-y]%mod;}
signed main()
{
n=read(); init();
for(int i=1;i<=n;i++) fro[i]=read(); sort(fro+1,fro+n+1); reverse(fro+1,fro+n+1);
for(int i=1;i<=n;i++) nex[i]=read(); sort(nex+1,nex+n+1); reverse(nex+1,nex+n+1);
while(pos1<=n||pos2<=n)
{
int tot=0,temp=max(fro[pos1],nex[pos2]),cnt1,cnt2,pre1=pos1,pre2=pos2;
while(pos1<=n&&fro[pos1]==temp) pos1++; cnt1=pos1-pre1;
while(pos2<=n&&nex[pos2]==temp) pos2++; cnt2=pos2-pre2;
for(int i=0,base=1;i<=cnt1;i++,base*=-1) tot=(tot+base*C(cnt1,i)*power(power(temp,i)*(power(temp+1,pos1-i-1)-power(temp,pos1-i-1)+mod),cnt2)%mod*power(power(temp,i)*power(temp+1,cnt1-i),pos2-cnt2-1)%mod+mod)%mod;
ans=ans*tot%mod;
}
printf("%lld",ans);
return 0;
}
T3 Seat
解题思路
好像并不是特别可做,于是果断去颓 skyh 学长的 blog 了。。
DP 数组的含义和题解上一样 \(f_{i,j}\) 表示已经坐下了 \(i\) 个人,还剩下 \(j\) 个长度为偶数区间的区间的概率。
首先处理出一组可行的解来,也就是代码里 20 到 31 行所做的事情。
然后枚举区间长度,对于每一种存在的区间长度,枚举所剩下的人,以及所剩下的长度为偶数的区间。
对于这一次选择的是奇数或者偶数的区间分别进行转移,注意这里的偶数的区间有两个位置可供选择。
然后再对于偶数区间进行一些特殊处理,然后这个题解就愉快地水过去了;
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Failed"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e3+50,M=3e4+10;
int n,mod,sum,pos[N],tot[N],odd[N],f[N][N],g[N][N],ans[N][N],inv[M];
bool vis[N];
signed main()
{
sum=n=read(); mod=read(); inv[1]=1; vis[0]=vis[n+1]=true;
for(int i=2;i<mod;i++) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
for(int i=1;i<=n;i++)
{
int l=0,r=0,mx;
for(int j=0,id=1;j<=n;j++,id=j+1)
{
while(!vis[id]) id++;
if(id-j>r-l) l=j,r=id;
j=id-1;
}
mx=(r-l)>>1; tot[mx]++; odd[mx]+=!((r-l-1)&1);
pos[i]=l+mx; vis[pos[i]]=true;
}
for(int i=sum-tot[1]+1;i<=sum;i++)
for(int j=sum-tot[1]+1;j<=sum;j++)
ans[i][pos[j]]=inv[tot[1]];
sum-=tot[1];
for(int i=2;i<=n;i++)
if(tot[i])
{
int fro=sum-tot[i]+1,to=sum,id=fro+odd[i]-1;
for(int j=0;j<=tot[i];j++) fill(f[j]+0,f[j]+odd[i]+1,0); f[0][odd[i]]=1;
for(int j=1,ow=0,ew=0;j<=tot[i];j++,ow=0,ew=0)
{
for(int k=0;k<=odd[i];k++)
if(f[j-1][k])
{
int res=(tot[i]-j+1)+k,temp;
if(k)
{
temp=f[j-1][k]*k%mod*2*inv[res]%mod;
(ow+=temp*inv[odd[i]*2])%mod;
f[j][k-1]=(f[j][k-1]+temp)%mod;
}
if(tot[i]-odd[i])
{
temp=f[j-1][k]*(res-2*k+mod)%mod*inv[res]%mod;
(ew+=temp*inv[tot[i]-odd[i]])%=mod;
f[j][k]=(f[j][k]+temp)%mod;
}
}
for(int k=fro;k<=id;k++)
ans[fro+j-1][pos[k]]=(ans[fro+j-1][pos[k]]+ow)%mod,
ans[fro+j-1][pos[k]+1]=(ans[fro+j-1][pos[k]+1]+ow)%mod;
for(int k=id+1;k<=to;k++) ans[fro+j-1][pos[k]]=(ans[fro+j-1][pos[k]]+ew)%mod;
}
for(int j=fro;j<=id;j++)
{
int l=pos[j]-i+1,r=pos[j]+i;
for(int p=l;p<=r;p++)
if(p!=pos[j])
for(int q=to+1,temp=(p<pos[j])?p+i+1:p-i,val=ans[q][p]*inv[2]%mod;q<=n;q++,temp=(p<pos[j])?p+i+1:p-i,val=ans[q][p]*inv[2]%mod)
g[q][p]=(g[q][p]+val)%mod,g[q][temp]=(g[q][temp]+val)%mod;
for(int p=l;p<=r;p++)
for(int q=to+1;q<=n;q++)
ans[q][p]=g[q][p],g[q][p]=0;
}
sum-=tot[i];
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++) printf("%lld ",ans[i][j]);
printf("\n");
}
return 0;
}

