8.26考试总结(NOIP模拟48)[Lighthouse·Miner·Lyk Love painting·Revive]
告诉我,神会流血吗?——神不会,但你会。
前言
我直接打娱乐赛
T1 Lighthouse
解题思路
子集反演(但是 fengwu 硬要说是二项式反演咱也没法。。。)
发现其实 \(m\) 的值非常的小,因此我们可以选择 状压 。
设 \(f_{i}\) 表示将应该删除掉的边至少保留 \(i\) 条的方案数。
那么表示恰好的 \(g_i\) 就可以由子集反演得到,因此最后的答案就是 \(g_0\)
对于当前算到的子集中有超过两条边有公共点,或者两个点之间有超过两种路径就是不合法的,这样显然是构成了环的。
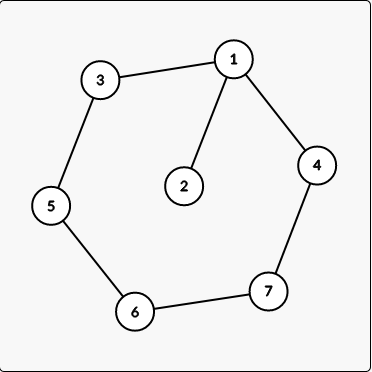
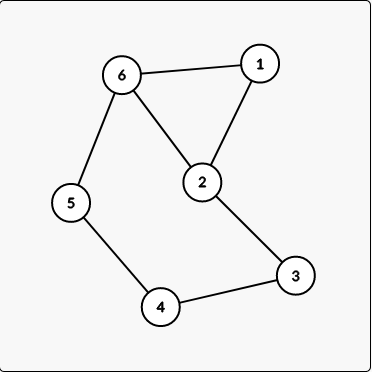
然后如果要构成一个长度为 n 的大环的话,除了当前选到的边,其他的可以直接圆排列。
对于选中的这几条边而言,因为整个图是一个完全图,因此他们的正负都是可以的,因此就有了 \(2^{选中边数}\) 种选择。
但是要注意如果将所有的边都翻转是和不反转一样的,因此需要将方案数除以 2
最后就是特盘一下边的集合组成的是一个长度为 \(n\) 的环的情况就好了。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e7+10,M=30,mod=1e9+7;
int n,m,top,ans,sta[N],fac[N],p2[N];
int u[M],v[M],vis[N],f[M];
int power(int x,int y)
{
int temp=1;
while(y)
{
if(y&1) temp=temp*x%mod;
x=x*x%mod;
y>>=1;
}
return temp;
}
signed main()
{
n=read();m=read(); fac[0]=p2[0]=1;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;
for(int i=1;i<=n;i++) p2[i]=p2[i-1]*2%mod;
for(int i=1;i<=m;i++) u[i]=read(),v[i]=read();
for(int st=0;st<(1<<m);st++)
{
int e=0,p=0;bool jud=false;
for(int i=1;i<=m;i++)
if((st>>i-1)&1)
{
e++;
if(vis[u[i]]==2||vis[v[i]]==2){jud=true;break;}
if(!vis[u[i]]) p++; vis[u[i]]++;
if(!vis[v[i]]) p++; vis[v[i]]++;
}
for(int i=1;i<=top;i++) if((st&sta[i])==sta[i]){jud=true;break;}
if(e==p&&!jud&&st)
{
jud=true; sta[++top]=st;
if(e==n) f[e]=(f[e]+2)%mod;
}
for(int i=1;i<=m;i++) vis[u[i]]=vis[v[i]]=0;
if(!jud) f[e]=(f[e]+fac[n-e-1]*p2[p-e])%mod;
}
for(int i=0,bas=1;i<=m;i++,bas*=-1) ans=(ans+mod+bas*f[i]*power(2,mod-2)%mod)%mod;
printf("%lld",ans);
return 0;
}
T2 Miner
解题思路
欧拉路,实在是调吐了。。。
对于每一个联通块里的出度奇数点每走一次最多使两个出度为奇数的点变为偶数。
因此,答案就是 \(\sum\limits_{i=1}^{k}\max(1,\dfrac{siz_i}{2})-1\),\(siz_i\) 表示每一个联通块里的出度计数点个数,\(k\) 为联通块个数。
然后对于整个图跑欧拉路,优先跑 出度为奇数 的点。
接下来我就被建边顺序给卡了,然后我就试了一下 random_shuffle 可以获得 \(63pts\sim 84pts\) 不等的分数,主要是他还可能会。。

然后我又试了试将 vector 建边通过翻转变成了前向星建边的顺序,然后发现一直不对的点对了!!!
在然后嘞,测试点分治。。(应该是我的做法有问题。。)
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=3e5+10;
int n,m,tot=1,cnt,first,all,Ans,top,sta[N<<1],fa[N],du[N],siz[N],head[N];
pair<bool,int> ans[N<<1];
vector<pair<int,int> > v[N];
bool vis[N<<1],work;
struct Road
{
int l,r;
}pat[N];
void add_edge(int x,int y)
{
v[x].push_back(make_pair(y,++tot));
}
int find(int x)
{
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
void oula(int fro)
{
bool flag=true,jud=true;
for(int i=head[fro];i<v[fro].size();i++)
if(!vis[v[fro][i].second])
flag=false;
if(flag) return head[fro]=v[fro].size(),void();
ans[++all]=make_pair(1,fro);
int pree=all;
sta[++top]=fro;
Ans--;
while(top)
{
int x=sta[top],pre=top;
if(jud||work||Ans<=0)
for(int i=head[x];i<v[x].size();i++)
{
int to=v[x][i].first;
if(vis[v[x][i].second]){head[x]=i+1;continue;}
vis[v[x][i].second^1]=vis[v[x][i].second]=true;
sta[++top]=to; head[x]=i+1;
du[x]--;du[to]--;
if(to!=x)break;
}
if(pre==top)
{
top--; jud=false;
if(top) ans[++all]=make_pair(0,x);
}
}
reverse(ans+pree+1,ans+all+1);
}
signed main()
{
n=read(); m=read(); srand(time(0));
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1,x,y;i<=m;i++)
{
x=read(); y=read();
pat[i].l=x;pat[i].r=y;
add_edge(pat[i].l,pat[i].r);
add_edge(pat[i].r,pat[i].l);
fa[find(pat[i].l)]=find(pat[i].r);
if(x!=y) du[pat[i].r]++,du[pat[i].l]++;
}
first=pat[1].l;
for(int i=1;i<=n;i++)
if(du[i]&1)
siz[find(i)]++;
for(int i=1;i<=n;i++)
if(find(i)==i&&v[i].size())
Ans+=max(1ll,siz[i]/2);
printf("%lld\n",max(0ll,Ans-1));
for(int i=1;i<=n;i++)
{
if(first!=71131)reverse(v[i].begin(),v[i].end());
for(int j=1,fir=0;j<v[i].size();j++)
{
int to=v[i][j].first;
if(to!=i) continue;
swap(v[i][j],v[i][fir]);
fir++;
}
}
for(int i=1,x,y;i<=m;i++)
if(pat[i].l==pat[i].r)
du[pat[i].l]+=2;
for(int i=1;i<=n;i++)
if(head[i]<v[i].size()&&(du[i]&1))
oula(i);
for(int i=1;i<=n;i++)
if(head[i]<v[i].size()&&du[i])
{
work=true;
oula(i);
}
printf("%lld\n",ans[1].second);
for(int i=2;i<=all;i++)
printf("%d %lld\n",ans[i].first,ans[i].second);
return 0;
}
T3 Lyk Love painting
解题思路
二分答案+DP
考场是是写挂了的,本来想降低一个 \(n\) 的复杂度,没想到弄巧成拙,喜提 \(10pts\)
60pts 的做法是 \(f_{i,j,k}\) 表示第 i 行从 j 到 k 的一段区间内的最优解,更新比较简单,向前跳看区域是否符合当前的二分值就好了。
然后再搞一个 \(g_i\) 表示两行一共到 位置 i 的最小划分数,转移和上面差不多,复杂度 \(n^3log\)
80pts 就比较理智了,先处理出第一行,第二行,两行一共,可以向前跳的最长长度,分别记为 \(f1_i,f2_i,f3_i\)。
然后 \(g_{i,j}\) 表示第一行在 i 位置,第二行在 j 位置的最小划分数。转移就是:
对于 \(i=j\) 的情况还可由 \(g_{f3_i,f3_j}+1\) 转移过来复杂度是 \(n^2log\) 的。
优化一下,发现最大就可以向前面跳 \(m\) 下每次选择下标较大的向前跳,统计答案就好了。
code
60pts
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+10,M=1e3+10,INF=1e18;
int n,m,pre[3][N],s[3][N];
int f[3][M][M],g[N];
bool check(int x)
{
memset(f,0x3f,sizeof(f));
memset(g,0x3f,sizeof(g));
g[0]=0;
for(int i=1;i<=2;i++)
for(int l=1;l<=n;l++)
{
f[i][l][l-1]=0;
for(int j=l;j<=n;j++)
for(int k=j-1;k>=l-1;k--)
if(pre[i][j]-pre[i-1][j]-pre[i][k]+pre[i-1][k]<=x) f[i][l][j]=min(f[i][l][j],f[i][l][k]+1);
else break;
}
if(f[1][1][n]+f[2][1][n]<=m) return true;
for(int i=1;i<=n;i++)
for(int j=i-1;j>=0;j--)
if(pre[2][i]-pre[2][j]<=x) g[i]=min(g[i],min(g[j],f[1][1][j]+f[2][1][j])+1);
else g[i]=min(g[i],g[j]+f[1][j+1][i]+f[2][j+1][i]);
if(g[n]<=m) return true;
return false;
}
signed main()
{
n=read(); m=read();
for(int i=1;i<=2;i++)
for(int j=1;j<=n;j++)
s[i][j]=read();
for(int i=1;i<=2;i++)
for(int j=1;j<=n;j++)
pre[i][j]=pre[i][j-1]+pre[i-1][j]-pre[i-1][j-1]+s[i][j];
int l=0,r=pre[2][n],ans=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
printf("%lld",ans);
return 0;
}
80pts
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+10,M=3e3+10,INF=1e18;
int n,m,pre[N],s1[N],s2[N],pre1[N],pre2[N];
int f1[N],f2[N],f3[N],g[M][M];
bool check(int x)
{
memset(g,0x3f,sizeof(g)); g[0][0]=0;
for(int i=1;i<=n;i++)
{
int temp=-1;
for(int j=i;j>=1;j--)
if(pre1[i]-pre1[j]<=x&&pre1[i]-pre1[j-1]>x)
{
temp=j;
break;
}
if(~temp) f1[i]=temp;
else f1[i]=0;
}
for(int i=1;i<=n;i++)
{
int temp=-1;
for(int j=i;j>=1;j--)
if(pre2[i]-pre2[j]<=x&&pre2[i]-pre2[j-1]>x)
{
temp=j;
break;
}
if(~temp) f2[i]=temp;
else f2[i]=0;
}
for(int i=1;i<=n;i++)
{
int temp=-1;
for(int j=i;j>=1;j--)
if(pre[i]-pre[j]<=x&&pre[i]-pre[j-1]>x)
{
temp=j;
break;
}
if(~temp) f3[i]=temp;
else f3[i]=0;
}
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++)
{
if(!i&&!j) continue;
g[i][j]=min(g[f1[i]][j],g[i][f2[j]])+1;
g[i][j]=min(g[i][j],g[max(f1[i],f2[j])][max(f1[i],f2[j])]+2);
if(i==j) g[i][j]=min(g[i][j],g[f3[i]][f3[j]]+1);
}
return g[n][n]<=m;
}
signed main()
{
n=read(); m=read();
for(int i=1;i<=n;i++) s1[i]=read();
for(int i=1;i<=n;i++) s2[i]=read();
for(int i=1;i<=n;i++) pre[i]=pre[i-1]+s1[i]+s2[i];
for(int i=1;i<=n;i++) pre1[i]=pre1[i-1]+s1[i];
for(int i=1;i<=n;i++) pre2[i]=pre2[i-1]+s2[i];
int l=0,r=pre[n],ans=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
printf("%lld",ans);
return 0;
}
正解
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+10,M=3e3+10,INF=1e18;
int n,m,pre[N],s1[N],s2[N],pre1[N],pre2[N];
int f1[N],f2[N],f3[N],g[N];
bool check(int x)
{
memset(g,0x3f,sizeof(g)); g[0]=0;
for(int i=1;i<=n;i++)
{
f1[i]=f1[i-1];
for(int j=f1[i]-1;j<i;j++)
if(pre1[i]-pre1[j+1]<=x)
{
f1[i]=j+1;
break;
}
}
for(int i=1;i<=n;i++)
{
f2[i]=f2[i-1];
for(int j=f2[i]-1;j<i;j++)
if(pre2[i]-pre2[j+1]<=x)
{
f2[i]=j+1;
break;
}
}
for(int i=1;i<=n;i++)
{
f3[i]=f3[i-1];
for(int j=f3[i]-1;j<i;j++)
if(pre[i]-pre[j+1]<=x)
{
f3[i]=j+1;
break;
}
}
for(int i=1;i<=n;i++)
{
g[i]=g[f3[i]]+1;
int pos1=i,pos2=i;
for(int j=1;j<=m&&(pos1||pos2);j++)
{
if(f2[pos2]>f1[pos1]||f1[pos1]==pos1) pos2=f2[pos2];
else pos1=f1[pos1];
g[i]=min(g[i],g[max(pos1,pos2)]+j);
}
}
return g[n]<=m;
}
signed main()
{
n=read(); m=read();
for(int i=1;i<=n;i++) s1[i]=read();
for(int i=1;i<=n;i++) s2[i]=read();
for(int i=1;i<=n;i++) pre[i]=pre[i-1]+s1[i]+s2[i];
for(int i=1;i<=n;i++) pre1[i]=pre1[i-1]+s1[i];
for(int i=1;i<=n;i++) pre2[i]=pre2[i-1]+s2[i];
int l=0,r=pre[n],ans=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
printf("%lld",ans);
return 0;
}

