7.18考试总结(NOIP模拟19)[u·v·w]
我们不是狼,我们只是长着獠牙的羊......
前言
我真 TM 爱死 \(\frac{1}{4}\) 了。
老实说,这套题是真恶心,第一题还有一点思路,到了后面是一点都搞不定了。
总的来说,主要原因是最近几天状态有些不好,需要及时调整。。
T1 u
解题思路
主要就是二维差分,对于一般的差分而言,都是以行和列进行差分。
由于这个题是一个直角三角形,因此我们需要改变一下差分的“方向”。
对于列和斜的方向进行差分(假设 1 数组为列方向的差分数组, 2 数组为斜着的),以下图为例。
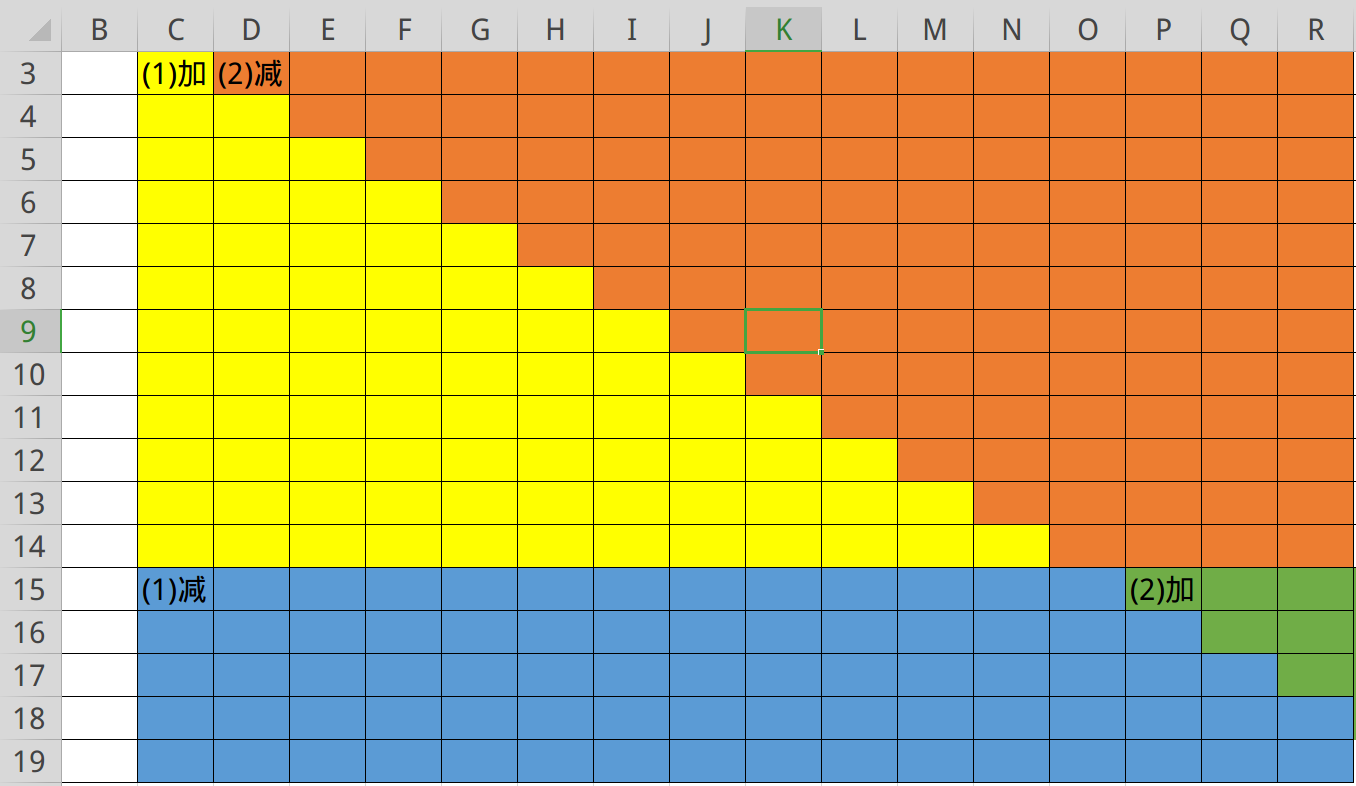
当我们需要给黄色区域加上数时,先给 \((3.C)\) 位置的 1 加上,那我们就相当与给所有的有颜色的位置都加上了。
因此在 \((15,C)\) 位置的 1 减去就可以除去在蓝色以及绿色区域多加上的数。
接下来考虑如何除去橙色部分的影响,可以看作这个大的三角形减去绿色部分。
于是就可以给 \((3,D)\) 位置的 2 减去,给 \((15,P)\) 位置的 2 加上就好了。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch>'9'||ch<'0')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
const int N=1e3+10;
int n,m,ans,q1[N][N],q2[N][N];
void solve(int x,int y,int len,int num)
{
q1[x][y]+=num;
if(y+1<=n) q2[x][y+1]-=num;
if(x+len<=n)
{
q1[x+len][y]-=num;
if(y+len+1<=n)
q2[x+len][y+len+1]+=num;
}
}
signed main()
{
n=read();
m=read();
for(int i=1,x,y,len,num;i<=m;i++)
{
x=read();
y=read();
len=read();
num=read();
solve(x,y,len,num);
}
for(int i=1;i<=n;i++)
{
int num=0;
for(int j=1;j<=n;j++)
{
q1[i][j]+=q1[i-1][j];
q2[i][j]+=q2[i-1][j-1];
num+=q1[i][j]+q2[i][j];
ans^=num;
}
}
printf("%lld",ans);
return 0;
}
T2 v
解题思路
正解比较简单粗暴。。
其实就是记忆化状压暴搜,有一个需要注意的点就是对于比较小的用数组,大的用 map 这样可以大大缩小空间。
当然也可以“特判”过。。(不难发现当序列中白色和黑色数量相同时,并且操作数为 n 或者 n-1 的时候期望值一定是\(\dfrac{n}{2}\))
然后对于状压中去除第 i 位并且将它之后的向左移一位的操作有两种实现:
(sta>>i<<i-1)|(sta&(1<<i-1)-1)(sta>>1&~((1<<i-1)-1))|(sta&(1<<i-1)-1)
然后,也就没啥好说的了。。。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch>'9'||ch<'0')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
const int N=35;
map<int,double> f[N];
int n,m,s;
string ch;
double dfs(int sta,int pos)
{
if(pos==n-m) return 0;
if(f[pos].find(sta)!=f[pos].end()) return f[pos][sta];
double sum=0;
for(int i=1;i<=pos/2;i++)
{
int clo1=(sta>>(i-1))&1,clo2=(sta>>(pos-i))&1;
int t1=(sta>>i<<i-1)|(sta&(1<<i-1)-1);
int t2=(sta>>(pos-i+1)<<pos-i)|(sta&((1<<pos-i)-1));
sum+=2*max(dfs(t1,pos-1)+clo1,dfs(t2,pos-1)+clo2);
}
if(pos&1)
{
int i=(pos+1)/2;
int clo=(sta>>(i-1))&1;
int temp=(sta>>1&~((1<<i-1)-1))|(sta&(1<<i-1)-1);
sum+=dfs(temp,pos-1)+clo;
}
sum=sum/(1.0*pos);
f[pos][sta]=sum;
return sum;
}
void check()
{
if(n&1||(m!=n-1&&m!=n))
return ;
int h=0,b=0;
for(int i=0;i<n;i++)
if(ch[i]=='W') b++;
else h++;
if(h!=b) return ;
printf("%.10lf",(double)n/2.0);
exit(0);
}
signed main()
{
n=read();
m=read();
cin>>ch;
check();
for(int i=1;i<=n;i++)
s=(s<<1)|(ch[i-1]=='W');
printf("%.20lf",dfs(s,n));
return 0;
}
T3 w
解题思路
树形 DP 设 f[i][1/0] 表示节点 i 是否与父亲连边。
设我们要翻转的边集为S,那么我们的最少的路径条数就是这个边集所能连接的点中度数为奇数的点的一半,
其实是那些可以配对为偶数的边都可以连成一条,所以只有奇数点才为路径的端点而且需要除以2
这样我们就会有一个状态了,状态中有两个量,一个是路径条数,一个是边的数量。
对于奇数点而言,其实就像相当与是好几对点,加上一个点,如果再加上一条边就不会增加操作次数。
偶数点也类似。对于 DP 方程的转移就好似 奇数+奇数=偶数 这一类的东西了。。。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch>'9'||ch<'0')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
const int N=1e5+10,M=N<<1,INF=1e9;
int n;
int tot,head[N],nxt[M],ver[M],edge[M];
struct Node
{
int opt,len;
Node friend operator + (Node x,Node y)
{
return (Node){x.opt+y.opt,x.len+y.len};
}
bool friend operator < (Node x,Node y)
{
if(x.opt!=y.opt)
return x.opt<y.opt;
return x.len<y.len;
}
}f[N][2];
void add_edge(int x,int y,int val)
{
ver[++tot]=y;
edge[tot]=val;
nxt[tot]=head[x];
head[x]=tot;
}
Node min(Node x,Node y)
{
if(x<y) return x;
return y;
}
void dfs(int x,int fa,int opt)
{
Node k1=(Node){INF,INF},k2=(Node){0,0};
for(int i=head[x];i;i=nxt[i])
{
int to=ver[i];
if(to==fa) continue;
dfs(to,x,edge[i]);
Node tmp1=min(k1+f[to][0],k2+f[to][1]);
Node tmp2=min(k1+f[to][1],k2+f[to][0]);
k1=tmp1;
k2=tmp2;
}
if(opt==1||opt==2) f[x][1]=min((Node){k1.opt,k1.len+1},(Node){k2.opt+1,k2.len+1});
else f[x][1]=(Node){INF,INF};
if(opt==0||opt==2) f[x][0]=min((Node){k1.opt+1,k1.len},k2);
else f[x][0]=(Node){INF,INF};
}
signed main()
{
n=read();
for(int i=1,x,y,c,d,temp;i<n;i++)
{
x=read();
y=read();
c=read();
d=read();
if(d==2) temp=2;
else temp=(c!=d);
add_edge(x,y,temp);
add_edge(y,x,temp);
}
dfs(1,0,2);
printf("%lld %lld",f[1][0].opt/2,f[1][0].len);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号