6.17考试总结(NOIP模拟8)[星际旅行·砍树·超级树·求和]
此身为剑所天成,身如钢铁,心似琉璃。
6.17考试总结(NOIP模拟8)
背景
考得不咋样,有一个非常遗憾的地方:最后一题少取膜了,\(100pts->40pts\),改了这么多年的错还是头一回看见以下的情景。。。
T1星际旅行
前言
考试的时候用一个自己感觉非常妙的思路骗了20pts,因为是双向边,所以分成两个边存,边的tot从2开始,这样可以保证没一组边的序号通过取\(xor\)可以相互转化。
然后对于每一个边记录经过次数,并且记一下经过次数为1和2的边的总数,然后对于dfs时转移的就是状压的每组边的状态,当然也可以拿Hash存。
做法挺妙的,唯一的缺点就是和正解一点关系都没有(逃
解题思路
正解主要是欧拉路的相关知识。
首先可以确定的是,如果这个图里面的各个边不是联通的话(可以用冰茶几或者DFS来判),那么总情况数一定是0,比如下图的情况:
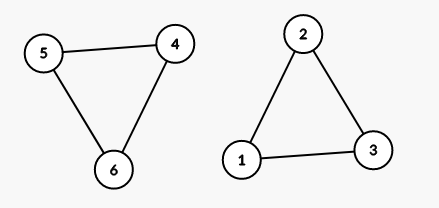
然后就是建立在欧拉路以及欧拉回路上面的东西了,
存在欧拉路的条件:图是连通的,有且只有2个奇点。
存在欧拉回路的条件:图是连通的,有0个奇点。
因此,问题就变成了把所有的边变成两条边之后,拆掉两条边使得新图仍然具有联通性,设自环数为\(cnt\),每个点的出入度为\(du[i]\),主要分为一下三种情况:
- 去掉任意2个自环:情况数为\(\dfrac{cnt\times(cnt-1)}{2}\)
- 去掉一个自环和一条边:情况数为:\(\dfrac{cnt \times \sum\limits_{i=1}^ndu_i}{2}\)
- 去掉两个有公共点的边:情况数为\(\dfrac{\sum\limits_{i=1}^n du_i \times (du_i-1)}{2}\)
记得开long long
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10,M=N<<1;
int n,m,link=N-1,sum,sum1,sum2,sum3,du[N],rdu[N],fa[N];
int find(int x)
{
if(fa[x]==x)
return x;
return fa[x]=find(fa[x]);
}
#undef int
int main()
{
#define int register long long
#define ll long long
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1,x,y;i<=m;i++)
{
scanf("%lld%lld",&x,&y);
if(x==y)
{
sum++;
rdu[x]++;
rdu[y]++;
continue;
}
du[x]++;
du[y]++;
rdu[x]++;
rdu[y]++;
x=find(x);
y=find(y);
fa[x]=y;
}
for(int i=1;i<=n;i++)
if(rdu[i])
{
link=i;
find(i);
break;
}
for(int i=1;i<=n;i++)
if(rdu[i]&&find(i)!=fa[link])
{
printf("0");
return 0;
}
sum1=sum*(sum-1)/2;
for(int i=1;i<=n;i++)
{
sum2+=du[i];
sum3+=du[i]*(du[i]-1)/2;
}
sum2=sum2*sum/2;
printf("%lld",sum1+sum2+sum3);
return 0;
}
T2 砍树
前言
考试的时候想到了二分答案,以为自己要切题了,然后考试结束前20分钟的时候突然就搞出来一个反例,不满足单调性,但是时间又不够了,我就草草的在错误答案的基础上改了一下,骗了20pts
解题思路
首先说一下为什么不满足单调性,显然的天数与希望树木的高度是有倍数关系的。。
问题就是让我们求一个最大的\(d\),满足:
移一下项,令\(T=k+\sum\limits_{i=1}^na_i\),可得:
然后我们就可以愉快的整除分块,暴力枚举每一个d然后判断是否符合条件就好了,显然的,对于每一个块里,右端点是最优解。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=110;
int n,m,ans,temp,s[N];
#undef int
int main()
{
#define int register long long
#define ll long long
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
scanf("%lld",&s[i]);
for(int i=1;i<=n;i++)
temp+=s[i];
temp+=m;
for(int l=1,r;l<=temp;l=r+1)
{
r=temp/(temp/l);
int sum=0;
for(int i=1;i<=n;i++)
sum+=ceil(1.0*s[i]/(1.0*r));
if(sum<=temp/r)
ans=r;
}
printf("%lld",ans);
return 0;
}
T3 超级树
前言
挺难的一道题,我考场上几乎是直接输出的样例,5pts,不知道是根据dp方程出的题还是出题人真的太强了,想出来的。。。
解题思路
首先要明白dp数组的含义:
dp[i][j]表示一棵i-超级树,有j条点不重复的路径的方案数
何为j条点不重复的路径?
在j条路径中,各个路径没有相交的部分(相同的点)。
考虑从dp[i]转移到dp[i+1],有五种转移状态
-
什么也不做:\(dp[i+1][l+r]+=num\)
-
根自己作为一条新路径 \(dp[i+1][l+r+1]+=num\)
-
根连接到左子树(或右子树)的某条路径上 \(dp[i+1][l+r]+=2 \times num \times (l+r)\)
-
根连接左子树和右子树的各一条路径 \(dp[i+1][l+r-1]+=2 \times num \times l\times r\)
-
根连接左子树(或右子树)的两条路径 \(dp[i+1][l+r-1]+=num \times (l \times (l-1)+r \times (r-1))\)
边界为dp[1][0]=dp[1][1]=1,答案为dp[k][1]。
看起来第二维状态可能有\(2^k\)那么大,但注意到从dp[i]转移到dp[i+1]时,路径的条数最多减少1条,因此第二维只有k个状态对最终的状态有影响,只dp这些状态即可。
- 注意:取\(\bmod\)运算不要太多,否则会TLE
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=610;
int n,mod,f[N][N];
#undef int
int main()
{
#define int register long long
#define ll long long
scanf("%lld%lld",&n,&mod);
f[1][0]=f[1][1]=1;
for(int dep=1;dep<n;dep++)
for(int i=0;i<=n;i++)
for(int j=0;j<=n-i;j++)
{
int num=f[dep][i]*f[dep][j]%mod;
f[dep+1][i+j]=(f[dep+1][i+j]+num)%mod;
f[dep+1][i+j+1]=(f[dep+1][i+j+1]+num)%mod;
f[dep+1][i+j]=(f[dep+1][i+j]+2*num*(i+j))%mod;
f[dep+1][i+j-1]=(f[dep+1][i+j-1]+2*num*i*j)%mod;
f[dep+1][i+j-1]=(f[dep+1][i+j-1]+num*(i*(i-1)+j*(j-1)))%mod;
}
printf("%lld",f[n][1]%mod);
return 0;
}
P4427 [BJOI2018]求和
前言
就这板子题,我竟然没有赛场上切掉,还是太菜了。。
解题思路
比较简单,先处理一下各种k次方,在搞一下深度的前缀和,剩下的就是LCA了(倍增,Tarjan,树链剖分都可以),当然也可以直接暴力向上跳,至于为什么又快又对,就非常玄学了。。。
- 注意:取\(\bmod\)要到位
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+10,M=N<<1,mod=998244353;
int n,Q,dep[N],f[N][25],q[51][N],po[N][51];
int tot,head[N],nxt[M],ver[M];
void add_edge(int x,int y)
{
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
int ksm(int x,int y)
{
int temp=1;
while(y)
{
if(y&1)
temp=temp*x%mod;
y>>=1;
x=x*x%mod;
}
return temp;
}
void dfs(int x,int fa)
{
for(int i=head[x];i;i=nxt[i])
{
int to=ver[i];
if(to==fa)
continue;
dep[to]=dep[x]+1;
f[to][0]=x;
dfs(to,x);
}
}
void LCA_init()
{
dfs(1,0);
for(int j=1;j<=20;j++)
for(int i=1;i<=n;i++)
f[i][j]=f[f[i][j-1]][j-1];
}
int LCA_ask(int x,int y)
{
if(x==y)
return x;
if(dep[x]>dep[y])
swap(x,y);
for(int i=20;i>=0;i--)
if(dep[x]<=dep[f[y][i]])
y=f[y][i];
if(x==y)
return x;
for(int i=20;i>=0;i--)
if(f[x][i]!=f[y][i])
{
x=f[x][i];
y=f[y][i];
}
return f[x][0];
}
#undef int
int main()
{
#define int register long long
#define ll long long
scanf("%lld",&n);
for(int i=1,x,y;i<n;i++)
{
scanf("%lld%lld",&x,&y);
add_edge(x,y);
add_edge(y,x);
}
LCA_init();
for(int i=1;i<=n;i++)
{
po[i][0]=1;
for(int j=1;j<=50;j++)
po[i][j]=po[i][j-1]*i%mod;
}
for(int i=0;i<=50;i++)
for(int j=1;j<=n;j++)
q[i][j]=(q[i][j-1]+po[j][i])%mod;
scanf("%lld",&Q);
while(Q--)
{
int x,y,k,lca;
scanf("%lld%lld%lld",&x,&y,&k);
lca=LCA_ask(x,y);
printf("%lld\n",(((q[k][dep[x]]+q[k][dep[y]])%mod-q[k][dep[lca]]+mod)%mod-q[k][dep[f[lca][0]]]+mod)%mod);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号