6.11考试总结(NOIP模拟7)
和绝望,和睦相处
背景
时间分配与得分成反比,T1 20min 73pts,T2 1h 30pts,T3 2h 15pts(没有更新tot值,本来应该是40pts的,算是本次考试中最遗憾的地方了吧),改起来就是T3比较难改,其他的还好。。。
两位队爷没考,战神也出了点意外,让我们这些菜鸡钻了空子。


T1 匹配
前言
我就没想到模拟赛会出这种水题,正解的话hash与KMP都可以,只可惜我只留下20分钟给这题,实力有限,时间有限,就草草打了个暴力。出乎意料整到了\(73pts\)属实出乎意料。。
解题思路
就讲一下Hash的做法吧,至于KMP做法请参考@fengwu的blog。
对于A的前缀可以用常规方法直接依次算,使幂次方数随着下标的递增而递减,
但是为了迎合后面对于B后缀的计算,我们这里令幂次方随下标递增而递增,先初始化一下,整出base值的若干次方存入p数组,因此求出A的Hash:
然后对于B的后缀就可以直接从后往前正常扫就好了。
之后我们就可以直接A的前缀和B的后缀两个串直接判等了,数组要开的大一点。
code
#include<bits/stdc++.h>
#define int unsigned long long
using namespace std;
const int N=2e5+10,base=13331;
int T,n,m,ans,p[N],h1[N],h2[N];
char ch,s[N],s2[N];
bool vis[30];
#undef int
int main()
{
#define int unsigned long long
scanf("%llu",&T);
p[0]=1;
for(int i=1;i<N;i++)
p[i]=p[i-1]*base;
while(T--)
{
memset(vis,false,sizeof(vis));
ans=0;
scanf("%llu%llu",&n,&m);
scanf("%s",s+1);
getchar();
scanf("%c",&ch);
for(int i=1;i<=n;i++)
vis[s[i]-'a']=true;
if(!vis[ch-'a'])
{
cout<<0<<endl;
continue;
}
for(int i=1;i<=m;i++)
s2[i]=s[i];
s2[++m]=ch;
for(int i=1;i<=m;i++)
{
h1[i]=h1[i-1]+s[i]*p[i-1];
// cout<<h1[i]<<" "<<h1[i-1]<<" "<<s[i]<<" " <<p[i-1]<<endl;
}
// cout<<endl;
h2[m+1]=0;
for(int i=m;i>=1;i--)
h2[i]=h2[i+1]*base+s2[i];
/* for(int i=1;i<=m;i++)
cout<<h2[i]<<' ';*/
for(int len=m;len>=1;len--)
{
int ha1=h1[len],ha2=h2[m-len+1];
if(ha1==ha2)
{
ans=len;
break;
}
}
printf("%llu\n",ans);
}
return 0;
}
T2 回家
前言
考场上这个题第一眼就看出了是Tarjan割点,然后想了想Tarjan超出了我的能力范围,就老老实实打暴力骗分去了。。。
解题思路
解题思路来自@fengwu,有一种双端扫的感觉。。。
dfn[i]储存i的时间戳,low[i]表示i所在联通块的最早dfs到的点的时间戳(话说这东西Tarjan不是讲过吗)vis用于从n节点向上进行更新。(vis[n]要初始化为true)
然后从1节点开始进行dfs,所连通的节点的状态有两种情况:
-
该节点未被扫过: 先对于该节点进行dfs,然后更新现在节点的low值,如果vis[to]是true也就是联通节点可以走到n,向上更新现在节点的vis为true。如果现在节点的时间戳小于等于联通节点所在联通块的最小时间戳并且联通节点可以到达n节点,那么这个点就是一个必经点。
-
该节点被扫过:用联通节点的时间戳来更新现在节点的low,为什么不用联通节点的low呢,以下图为例:
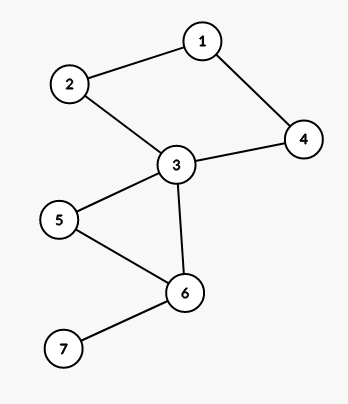
假设现在节点是6号节点,要扫3号节点了,3号节点的时间戳是7,low是1如果我们用low来更新,那无异与除7之外ia所有节点都是一个联通块的,这显然是不可以的。
最后输出就好了,注意必经点要排一下序。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
int T,n,m,cnt,tim,dian[N],dfn[N],low[N];
int tot,ver[N<<1],head[N],nxt[N<<1];
bool vis[N],b[N];
inline void add_edge(int x,int y)
{
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void init()
{
tot=cnt=tim=0;
memset(vis,false,sizeof(vis));
memset(head,0,sizeof(head));
memset(nxt,0,sizeof(nxt));
memset(ver,0,sizeof(ver));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
}
void dfs(int x)
{
dfn[x]=low[x]=++tim;
for(int i=head[x];i;i=nxt[i])
{
int to=ver[i];
if(!dfn[to])
{
dfs(to);
low[x]=min(low[to],low[x]);
if(vis[to])
vis[x]=true;
if(low[to]>=dfn[x])
if(x!=1&&vis[to])
dian[++cnt]=x;
}
else
low[x]=min(low[x],dfn[to]);
}
}
int main()
{
scanf("%d",&T);
while(T--)
{
init();
scanf("%d%d",&n,&m);
for(int i=m,x,y;i>=1;i--)
{
scanf("%d%d",&x,&y);
if(x==y)
{
m--;
continue;
}
add_edge(x,y);
add_edge(y,x);
}
vis[n]=true;
dfs(1);
sort(dian+1,dian+cnt+1);
printf("%d\n",cnt);
for(int i=1;i<=cnt;i++)
printf("%d ",dian[i]);
printf("\n");
}
return 0;
}
T3 寿司
前言
挺可惜的,考场上2h想到了40分的打法,也打出来了,就是tot没有清零喜提15pts。
解题思路
暴力
暴力的话40pts比较好想,先化环为链,再对于每一个长度为n的区间,先求一下每个R节点之前以及之后的R分别到两端的距离和,用前缀后缀和维护,然后对于移到左边的个数进行枚举,更新。设到左侧的个数为cnt,因为不是每一个点都要移到端点,不难发现我们需要减去一部分:
对于右端点的处理也是如此,优化的话就是二分一下对于区间的右半部分向右移,左半部分向左移,不难发现中间节点的坐标与区间是单调的,我们可以暴力处理第一个,对于后面的挨个搜就行了,还需要一个全局前缀和复杂度为\(O(n)\)但是我们打出来。。。可以参考 @zxb的代码,下面给出暴力的代码
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
int T,n,ans,tot,temp,cnt,ch[N],q[N],h[N];
char s[N<<1];
void work(int x)
{
// memset(q,0,sizeof(q));
// memset(h,0,sizeof(h));
int r=x-1,lb=0;
for(int i=x;i<=2*n;i++)
{
r++;
if(s[i]=='B')
lb++;
if(lb==tot)
break;
}
if(lb!=tot)
return ;
for(int i=x;i<=r;i++)
if(s[i]=='R')
{
ch[++cnt]=i;
q[cnt]=q[cnt-1]+i-x;
}
h[cnt+1]=0;
for(int i=cnt;i>=0;i--)
h[i]=h[i+1]+r-ch[i];
for(int i=0;i<=cnt;i++)
{
int sum=0;
sum=q[i]-(i+1-1)*(i-1)/2+h[i+1]-(cnt-i+1-1)*(cnt-i-1)/2;
if(sum>=0)
ans=min(ans,sum);
}
}
#undef int
int main()
{
#define int register long long
#define ll long long
scanf("%lld",&T);
while(T--)
{
ans=INT_MAX;
tot=0;
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;i++)
tot+=(s[i]=='B');
if(n-tot>tot)
{
for(int i=1;i<=n;i++)
s[i]=(s[i]=='B')?'R':'B';
tot=n-tot;
}
for(int i=1;i<=n;i++)
s[i+n]=s[i];
for(int i=1;i<=n;i++)
{
if(s[i]=='R')
continue;
temp=cnt=0;
work(i);
}
printf("%ld\n",ans);
}
return 0;
}
正解
思路非常的巧妙来自zhanshen@zero4338,l[i]表示i到左端点的距离(也就是该点左边B的个数)可以得出以下式子:
接下来我们只需要处理后半段就行了,对于后半段,我们先压入小根堆里,然后再对于B和R的情况分别进行处理:
- 扫到B字符:首先把B移到右边端点后所有的l都减了1,r都加了1,因此加上负数数量*2,我们需要将之前处理P字符的进行更新,如果堆顶的值大于扫过的B数量*2,直接break,剩下的交给后面处理,对于相等的,计算移动的R字符本身,给sum减去2,处理完堆里的之后再将正数的贡献加上就好了。
- 扫到R字符:先不做处理,将它的贡献压入堆里,然后更新正负数的值。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
int T,n,sum,maxn,tb,tr,z,f,tot,l[N],r[N];
char s[N];
priority_queue<int,vector<int>,greater<int> > q;
void init()
{
memset(l,0,sizeof(l));
memset(r,0,sizeof(r));
z=f=tb=tr=sum=tot=maxn=0;
while(!q.empty())
q.pop();
}
#undef int
int main()
{
#define int register long long
#define ll long long
scanf("%lld",&T);
while(T--)
{
init();
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;i++)
{
l[i]=l[i-1];
if(s[i]=='B')
{
tb++;
l[i]++;
}
else
tr++;
}
for(int i=1;i<=n;i++)
if(s[i]=='R')
{
r[i]=tb-l[i];
sum+=abs(l[i]-r[i]);
if(l[i]-r[i]>0)
{
q.push(l[i]-r[i]);
z++;
}
else f++;
}
maxn=max(maxn,sum);
for(int i=1;i<n;i++)
{
if(s[i]=='B')
{
sum+=2*f;
tot++;
while(!q.empty())
{
if(q.top()>2*tot)
break;
if(q.top()==2*tot)
sum-=2;
z--;
f++;
q.pop();
}
sum-=2*z;
maxn=max(maxn,sum);
}
else
{
z++;
f--;
q.push(tb+2*tot);
}
}
printf("%lld\n",(tr*tb-maxn)/2);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号