莫比乌斯反演 总结
我终不能改变那个开始,何不忘了那个结局呢。
莫比乌斯反演
洛谷题单
前置芝士
例题略解
P2257 YY的GCD
果然数论的题是真心不好搞。
第一个莫比乌斯反演的题,好好推一下式子吧。。(借鉴了blog)
我们要求的答案就是\(Ans=\sum\limits_{i=1}^{n}\sum\limits _{j=1}^{m}[\gcd(x,y)=prim]\)
这算是一类题了,大概套路如下:
-
\(f[d]\) 表示 \(\gcd(i,j)\) 所有的方案数。
即:\(f(d)=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}[gcd(i,j)=d]\)
-
\(F(n)\) 为 \(\gcd(i,j)=n\) 和 \(n\) 的倍数的个数
即:\(F(n)=\sum\limits_{n|d}f(d)=\lfloor\frac{N}{n}\rfloor\lfloor\frac{M}{n}\rfloor\)
也就是N中为n的倍数的数目与M中为n的倍数的数目的乘积就是所求的 F(n) 了。
-
根据以上的定义,莫比乌斯反演不难得出:
\(f(n)=\sum\limits_{n|d}\mu(\lfloor\frac{d}{n}\rfloor)F(d)\)
接下来就是化简式子了
\(Ans=\sum\limits_{p\in prim}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}[gcd(i,j)=p]\)
将\(f(p)\)带入上面式子:
\(Ans=\sum\limits_{p\in prim}f(p)\)
再用上面的式子3莫比乌斯反演一下:
\(Ans=\sum\limits_{p\in prim}\sum\limits_{p|d}\mu(\lfloor\frac{d}{p}\rfloor)F(d)\)
将之前给出的\(F(n)\)表达式带入,再更改一下循环顺序:
\(Ans=\sum\limits_{T=1}^{min(n,m)}\sum\limits_{t|T,t\in prime}\mu(\lfloor\frac{T}{t}\rfloor)\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor\)
\(Ans=\sum\limits_{T=1}^{min(n,m)}\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor(\sum\limits_{t|T,t\in prime}\mu(\lfloor\frac{T}{t}\rfloor))\)
最后,数论分块一下求一个前缀和就好了。
数论分块:
对于任意一个\(i(i \le n)\),我们需要找到一个最大的 \(j(i \le j \le n )\),使得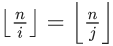
此时
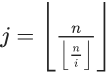
- 注意:只有ans开 long long就好了,都开的话会TLE
P3312 [SDOI2014]数表
又是一道数论毒瘤题 (好像数论题每一道都挺毒瘤).
LateX公式来自blog
我们要求的是
\(\displaystyle\sum_{i=1}^{n}\sum_{j=1}^{m} \sigma(\gcd(i,j))[ \sigma(\gcd(i,j)) \leq a]\)
和上一个题比较相似,先枚举一下gcd:
\(\displaystyle\sum_{d=1}^{n} \sigma(d)[\sigma(d) \leq a] \sum_{i=1}^{n}\sum_{j=1}^{m} [\gcd(i,j) == d]\)
在按老套路反演一下gcd:
\(\displaystyle\sum_{d=1} ^{n}\sigma(d) [\sigma(d)\leq a] \sum_{i=1}^{n\over d}\sum_{j=1}^{m\over d} [\gcd(i,j) == 1]\)
\(\displaystyle\sum_{d=1}^{n}\sigma(d)[\sigma(d) \leq a] \sum_{i=1}^{n\over d}\sum_{j=1}^{m\over d} \sum_{p|i,p|j}\mu(p)\)
\(\displaystyle\sum_{d=1}^{n}\sigma(d) [\sigma(d) \leq a] \sum_{p=1}^{n\over d} \mu(p) {n\over {dp}} {m\over dp}\)
将式子中的dp设为Q,并进行枚举:
\(\displaystyle\sum_{Q=1}^{n} {n\over Q}{m\over Q} \sum_{d\mid Q} \sigma(d)[\sigma(d)\leq a] \mu({n\over Q})\)
将式子的后半部分设为f
即:\(\displaystyle f(n) = \sum_{d\mid n} \sigma(d) \mu({n\over d})\)
然后再用树状数组,和数论分块进行一些处理就好了,
至于过程中的取mod,直接用unsigned int自然溢出,最后再按位与一下INT_MAX。
U164222 [BZOJ3309]DZY Loves Math
这个题相比上一个题来说就显得简单许多了,优化比较少。
总结一下套路打法吧:
- 列出原始式子
- 更改式子,枚举不同的gcd,然后通过\([\gcd(i,j)=1]=\sum\limits_{d|gcd(i,j)} \mu(d)\)将gcd转化成\(\mu\)
- 更改枚举的数值,把gcd干掉。
- 构建线性筛
- 前缀和与数论分块优化
- long long 慎开
本题的话就是\(\sum\limits_{T=1}^{\min(a,b)}\lfloor\frac{a}{T}\rfloor\lfloor\frac{b}{T}\rfloor\sum\limits_{d|T}f(d)\mu(\frac{T}{d})\)
然后线性筛一下f函数就行了。
- 注意:只有ans开 long long就好了,更新时要给其他的乘上1ll
P3327 [SDOI2015]约数个数和
LateX公式有点多,懒得打了,粘一篇别人的题解

P4449 于神之怒加强版
LateX公式来自于blog
和前面的题大同小异,显然可以得出以下式子:
\(\sum\limits_{T=1}^n\lfloor\dfrac{n}{T}\rfloor\lfloor\dfrac{m}{T}\rfloor\sum\limits_{d|T}d^k\mu(\dfrac{T}{d})\)
为了方便计算前缀和,令\(g(T)=\sum\limits_{d|T}d^k\mu(\dfrac{T}{d})\)
不难发现,这是个积性函数,于是我们进行如下推算:
\(g(T)=\prod\limits_{i=1}^t g(P_i^{x_i})\)
\(=\prod\limits_{i=1}^t(P_i^{k\times (x_i-1)}\times \mu(P_i)+P_i^{k\times x_i}\times \mu(1))\)
\(=\prod\limits_{i=1}^t P_i^{k\times (x_i-1)}\times(P_i^k-1)\)
第一行就是积性函数的性质,这里不予以过多说明。
第二行:因为\(P_i\)是质因数,所以\(P_i\)的因数只有1和他本身,式子的前半部分就是因数为本身的情况,后半部分就是因数为1的情况。
第三行:将第二行式子后半部分拆成\(P_i^{k\times(x-1)} \times P_i^k\times\mu(1)\),又因为\(\mu(1)=1,\mu(P_i)=-1\)便得出了最后的式子。
最后再按套路进行线性筛以及数论分块就好了。
P1829 [国家集训队]Crash的数字表格 / JZPTAB
显然\(lcm(x,y)=\dfrac{x\times y}{gcd(x,y)}\)
原式也就等价于\(\sum\limits_{i=1}^n\sum\limits_{j=1}^m\frac{i\cdot j}{\gcd(i,j)}\)
和原来的套路一样枚举\(gcd\),两个数除以\(gcd\)得到的数互质
\(\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{d|i,d|j,\gcd(\frac{i}{d},\frac{j}{d})=1}\frac{i\cdot j}{d}\)
把\(gcd\)化到分子上
\(\sum\limits_{d=1}^n d\cdot\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}[\gcd(i,j)=1]\cdot i\cdot j\)
后半段式子中,出现了互质数对之积的和,把它拿出来单独计算,计为\(sum\)。
即:\(\operatorname{sum}(n,m)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m [\gcd(i,j)=1]\cdot i\cdot j\)
接下来对 \(sum(n,m)\operatorname{sum}(n,m)sum(n,m)\) 进行化简。首先枚举约数,并将\([\gcd(i,j)=1]\) 表示为 \(\varepsilon(\gcd(i,j))\)
\(\sum\limits_{d=1}^n\sum\limits_{d|i}^n\sum\limits_{d|j}^m\mu(d)\cdot i\cdot j\)
设\(i=i'\cdot d,j=j'\cdot d\)(其中 i′,j′ 指上式中的 i,j),可以将式子变为:
\(\sum\limits_{d=1}^n\mu(d)\cdot d^2\cdot\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}i\cdot j\)
观察上式,前半段可以预处理前缀和;后半段又是一个范围内数对之和,因此:
\(g(n,m)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m i\cdot j=\frac{n\cdot(n+1)}{2}\times\frac{m\cdot(m+1)}{2}\)
可以\(\Theta(1)\)求解
\(\operatorname{sum}(n,m)=\sum\limits_{d=1}^n\mu(d)\cdot d^2\cdot g(\lfloor\frac{n}{d}\rfloor,\lfloor\frac{m}{d}\rfloor)\)
对\(\lfloor\dfrac{n}{\lfloor\frac{n}{d}\rfloor}\rfloor\)数论分块求\(\operatorname{sum}(n,m)\)函数
再看最上面的式子可得:
\(\sum\limits_{d=1}^n d\cdot\operatorname{sum}(\lfloor\frac{n}{d}\rfloor,\lfloor\frac{m}{d}\rfloor)\)
不难发现,这个式子也可以数论分块,总的复杂度为\(\Theta(n+m)\)
在线性筛的时候有两种打法:
- 先求出莫比乌斯函数,进而求出sum
- 直接线性求sum
方法二快于方法一,上面主讲方法一,hzoj方法二\(code\)
- 注意:取模上括号慎用!!!!,次序不同
P3704 [SDOI2017]数字表格
显然:
\(\begin{aligned}&\prod_{i=1}^{N}\prod_{j=1}^{M}F_{\gcd(i,j)} \\=&\prod_{k=1}^{N}{F_{k}}^{\left(\sum\limits_{i=1}^{N}\;\sum\limits_{j=1}^{M}\;\left[\gcd(i,j)=k\right]\right)}\end{aligned}\)
指数部分可以化乘为加:
\(\begin{aligned}&= \sum_{i=1}^{N}\sum_{j=1}^{M}\left[\gcd(i,j)=k\right]\\&= \sum_{i=1}^{\left\lfloor\frac{N}{k}\right\rfloor}\sum_{j=1}^{\left\lfloor\frac{M}{k}\right\rfloor}\left[\gcd(i,j)=1\right]\\&= \sum_{d=1}^{\left\lfloor\frac{N}{k}\right\rfloor}\mu(d)\left\lfloor\frac{N}{kd}\right\rfloor\left\lfloor\frac{M}{kd}\right\rfloor\end{aligned}\)
因此:
\(\begin{aligned} &= \prod_{k=1}^{N}{F_{k}}^{\left(\sum_{d=1}^{\left\lfloor\frac{N}{k}\right\rfloor}\mu(d)\left\lfloor\frac{N}{kd}\right\rfloor\left\lfloor\frac{M}{kd}\right\rfloor\right)}\\ &= \prod_{T=1}^{N}\left(\prod_{k|T}{F_{k}}^{\mu(\frac{T}{k})}\right)^{\left\lfloor\frac{N}{T}\right\rfloor\left\lfloor\frac{M}{T}\right\rfloor} \end{aligned}\)
令\(f(n)=\prod_{d|n}{F_{d}}^{\mu(\frac{n}{d})}\)
那么:\(=\prod_{T=1}^{N}{f(T)}^{\left\lfloor\frac{N}{T}\right\rfloor\left\lfloor\frac{M}{T}\right\rfloor}\)
外层数论分块,内层直接暴力干掉。
时间复杂度:\(\Theta(N(\log N+\log mod)+T\sqrt{N}\log mod)\)
P6271 [湖北省队互测2014]一个人的数论


