P2783 有机化学之神偶尔会做作弊

题面

思路：tarjan缩点+LCA。

根据题意，对于每一个C环我们肯定要进行tarjan无向图缩点。裸到不能再明显啊qwq。

最后我们缩出来的肯定一定是棵树。

显然对于同一条直链上的两个点我们很容易发现两个点之间C的数量为两个点的\(dep\)做差加\(1\)。

而对于这种情况:

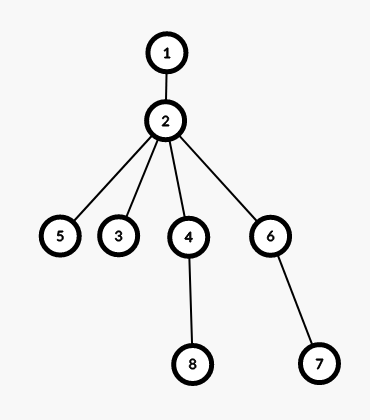
如果要查询\(5\)号点和\(7\)号点之间的C的数量，我们转化为\(5\)号点和\(2\)号点，\(2\)号点和\(7\)号点的情况即可。
其中\(2\)号点为\(5\)号点和\(7\)号点的LCA。

所以我们对缩完点之后的树进行树剖求一下LCA。

然后处理一下细节。

最后在进行输出时转化为2进制。

然后你就成功水了一道题qwq。

代码：

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1e5;

template<typename temp>void read(temp &x){
    x = 0;temp f = 1;char ch;
    while(!isdigit(ch = getchar())) (ch == '-') and (f = -1);
    for(x = ch^48; isdigit(ch = getchar()); x = (x<<1)+(x<<3)+(ch^48));
    x *= f;
}
template <typename temp, typename ...Args>void read(temp& a, Args& ...args){read(a), read(args...);}

int n, m, q, cnt, num, dfn[maxn], low[maxn], vis[maxn], color[maxn];

vector<int> v[maxn], edge[maxn];
stack<int> s;

struct poutree{
    int size[maxn], dep[maxn], height_son[maxn], fa[maxn], top[maxn];
    void build_poutree(int now){
        size[now] = 1;
        for(int i = 0; i < edge[now].size(); i ++){
            int to = edge[now][i];
            if(dep[to]) continue;
            dep[to] = dep[fa[to] = now] + 1;
            build_poutree(to);
            size[now] += size[to];
            if(size[to] > size[height_son[now]]) height_son[now] = to;
        }
    }
    void dfs(int now, int topfa){
        top[now] = topfa;
        if(height_son[now]) dfs(height_son[now], topfa);
        for(int i = 0; i < edge[now].size(); i ++){
            int to = edge[now][i];
            if(fa[now] == to or to == height_son[now]) continue;
            dfs(to,to);
        }
    }
    int lca(int x, int y){
        while(top[x] != top[y]){
            if(dep[top[x]] < dep[top[y]]) swap(x,y);
            x = fa[top[x]];
        }
        return dep[x]<dep[y]?x:y;
    }
    int dis(int x, int y){
	int cmp = lca(x, y);
	return dep[x]-dep[cmp]+dep[y]-dep[cmp];
    }
    void print(int now){
        if(!now) return;
        print(now>>1);
        printf("%d",now&1);
    }
    void ask(int x, int y){print((dis(color[x],color[y])+1)),printf("\n");} 
}tree;

inline void add_edge(int x, int y){
    edge[x].push_back(y);
    edge[y].push_back(x);
}

void tarjan(int now, int from){
    dfn[now] = low[now] = vis[now] = ++cnt;
    s.push(now);
    for(int i = 0; i < v[now].size(); i ++){
        int to = v[now][i];
        if(to == from) continue;
        if(!dfn[to]){
            tarjan(to, now);
            low[now] = min(low[to], low[now]);
        }else if(vis[to]) low[now] = min(low[now], dfn[to]);
    }
    if(dfn[now] == low[now]){
        ++num;
        while(1){
            int top = s.top();
            s.pop(), vis[top] = 0, color[top] = num;
            if(top == now) break;
        }
    }
}

signed main(){
    read(n, m);
    for(int i = 1, x, y; i <= m; i ++){
        read(x, y);
        v[x].push_back(y), v[y].push_back(x);
    }
    for(int i = 1; i <= n; i ++){
        if(!dfn[i]) tarjan(i,0);
    }
    for(int i = 1; i <= n; i ++){
        for(int j = 0; j < v[i].size(); j ++){
            int to = v[i][j];
            if(color[i] != color[to]) add_edge(color[i], color[to]);
        }
    }
    tree.build_poutree(1*(tree.dep[1]=1)), tree.dfs(1,1);
    read(q);
    for(int i = 1, x, y; i <= q; i ++){
        read(x,y);
        tree.ask(x,y);
    }
    return 0;
}