摘要：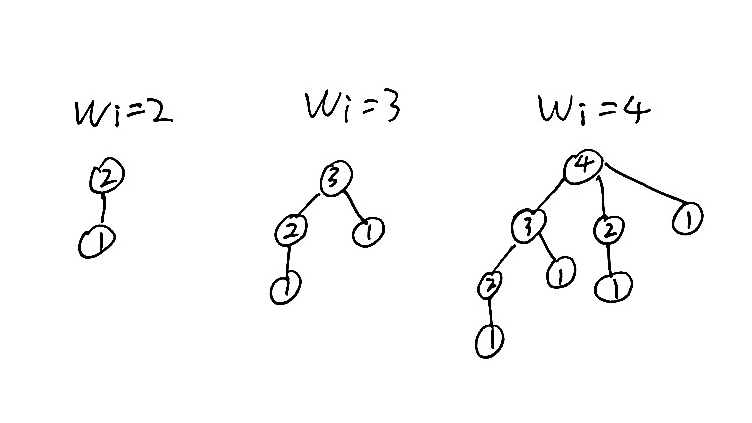 
这是一道再经典不过的树形DP了。太惭愧了。
怪物们在一棵有 $n$ 个顶点的树上，编号为 $i(1\le i\le n)$ 的怪物位于编号为 $i$ 的顶点上，攻击力为 $a_i$ 。你需要与怪物战斗 $10^{100}$ 个回合。在每个回合中，会依次发生以下两步：
1. 所有**活着的**怪物攻击你。你的生命值会按照**所有活体怪物攻击点的总和**减少。
2. 您选择一些（可以选全部，也可以不选）怪物并杀死它们。被杀死的怪物将不会再进行攻击。
限制条件：在一个回合内不能杀死相邻的两只怪物。
如果您以最佳选择方式攻击的怪物，那么在所有回合后，您的健康值减少的最小值是多少？
$1\le t\le 10^4,1\le n\le 3\cdot 10^5,1\le a_i \le 10^{12},\sum n\le 3\cdot 10^5$ 阅读全文
这是一道再经典不过的树形DP了。太惭愧了。
怪物们在一棵有 $n$ 个顶点的树上，编号为 $i(1\le i\le n)$ 的怪物位于编号为 $i$ 的顶点上，攻击力为 $a_i$ 。你需要与怪物战斗 $10^{100}$ 个回合。在每个回合中，会依次发生以下两步：
1. 所有**活着的**怪物攻击你。你的生命值会按照**所有活体怪物攻击点的总和**减少。
2. 您选择一些（可以选全部，也可以不选）怪物并杀死它们。被杀死的怪物将不会再进行攻击。
限制条件：在一个回合内不能杀死相邻的两只怪物。
如果您以最佳选择方式攻击的怪物，那么在所有回合后，您的健康值减少的最小值是多少？
$1\le t\le 10^4,1\le n\le 3\cdot 10^5,1\le a_i \le 10^{12},\sum n\le 3\cdot 10^5$ 阅读全文