The length of parametric curve (x + sin x, cos x)
问题引入
一个硬币（圆）的周长上有一个点，将硬币在一条线上无滑动地滚动。假设那个点开始时在最上面，滚了半圈到了最下面，求这个点相对于地面的运动轨迹的长度。
或者说，再简单点，自行车总骑过吧。假如你在骑自行车，自行车的轮胎最上缘有一个小石子，然后向前骑行，石子滚到了最下缘，求这个石子相对于地面的运动轨迹的长度。
初步计算
首先设半径为\(r\)，旋转的角度为\(\theta\)。
易得出位移为
\[x=\theta r+r\sin \theta\\
y=r\cos x
\]
可以在几何画板中画出对应的参数曲线
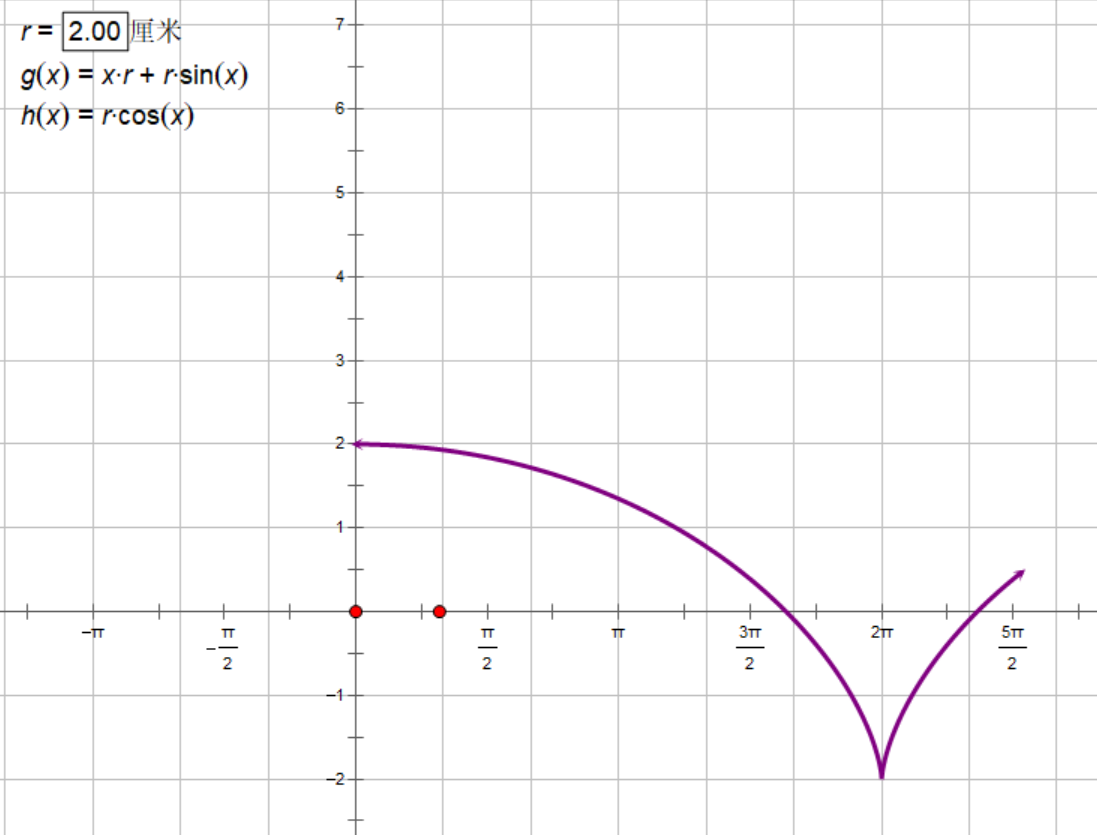
易得曲线的取值范围应当是小于其所在矩形的半周长，大于其对角线长度的，也就是\([\sqrt{4r^2+\pi^2},2r+\pi r]\)。
问问AI
不妨设\(r=1\)，把这个问题化简为The length of parametric curve (x + sin x, cos x)。
那么我们就得到了问题的近似解:\(S=4\).
欸？是个整数？
更进一步
这条曲线在数学中有很久远的研究，它就是大名鼎鼎的摆线Cycloid。
早在17世纪，人们就发现了摆线的几个性质：
- 它的长度等于旋转圆直径的 \(4\) 倍。尤为令人感兴趣的是，它的长度是一个不依赖于\(\pi\)的有理数。
- 在弧线下的面积，是旋转圆面积的三倍。
- 圆上描出摆线的那个点，具有不同的速度（事实上，在特定的地方它甚至是静止的）。
- 当弹子从一个摆线形状的容器的不同点放开时，它们会同时到达底部。
说句闲话，\(S=3πr^2\) 最初的证明是，找个均匀木板，切个圆，切个摆线，然后一看质量比 \(1:3\)。好像是伽利略干的
——\(\rm\color{red}{WYXkk}\)
而我们发现的就是其第一条性质了。
为了方便地用数学证明它，我们再次定义一下摆线。
设圆的半径为\(r=1\)，旋转角为\(t\)，那么参数曲线定义为
\[x=t-\sin t\\
y=1-\cos t
\]
计算曲线长度
\[\begin{align}
L&=\int_0^{2\pi}\sqrt{\mathrm{d}x^2+\mathrm{d}y^2}\\
&=\int_0^{2\pi}\sqrt{(1-\cos t)^2+\sin^2 t}\ \mathrm{d}t\\
&=\int_0^{2\pi}\sqrt{2-2\cos t}\ \mathrm{d}t\\
&=\int_0^{2\pi}2\mid \sin\frac t2\mid\ \mathrm{d}t\\
&=2\cdot\int_0^{2\pi}\sin\frac t2\times2\times\mathrm{d}\frac t2\\
&=4\cdot\int_0^\pi\sin t\ \mathrm{d}t\\
&=4
\end{align}
\]
计算面积
\[\begin{align}
S&=\int_0^{2\pi}y\ \mathrm{d}x\\
&=\int_0^{2\pi}(1-\cos t)^2\ \mathrm{d}t\\
&=\int_0^{2\pi}(1-2\cos t+\cos^2t)\ \mathrm{d}t\\
&=2\pi-0+\int_0^{2\pi}\cos^2t\ \mathrm{d}t\\
&=2\pi+\int_0^{2\pi}\sin^2t\ \mathrm{d}t\\
&=2\pi+\frac12\int_0^{2\pi}\sin^2t\ \mathrm{d}t+\frac12\int_0^{2\pi}\cos^2t\ \mathrm{d}t\\
&=2\pi+\frac12\int_0^{2\pi}\sin^2 t+\cos^2 t\\
&=3\pi
\end{align}
\]
EOF
