《数据结构》课程作业

第二章

PTA编程题

一共十道编程题

难度排序：

\[\begin{align} 6<8<5'<7<5<10<1=2<3\le 4<9 \nonumber \end{align} \]

6-1 有序链表合并（无重复）

双指针法

def merge_list(la, lb):
    ans = LinkList()
    p = ans.head

    p1 = la.head.next
    p2 = lb.head.next

    while p1 is not None and p2 is not None:
        if p1.data < p2.data:
            p.next = p1
            p1 = p1.next
        elif p1.data > p2.data:
            p.next = p2
            p2 = p2.next
        else:
            p.next = p1
            p1 = p1.next
            p2 = p2.next
        p = p.next
    if p1 is not None:
        p.next = p1
    elif p2 is not None:
        p.next = p2
    return ans

6-2 有序链表合并（可重复）

同上，也是双指针法。与6-1差异较小

def merge_list(la, lb):
    ans = LinkList()
    p = ans.head

    p1 = la.head.next
    p2 = lb.head.next

    while p1 is not None and p2 is not None:
        if p1.data < p2.data:
            p.next = p1
            p1 = p1.next
        else:
            p.next = p2
            p2 = p2.next
        p = p.next
    if p1 is not None:
        p.next = p1
    elif p2 is not None:
        p.next = p2
    return ans

6-3 集合交集

还是双指针法

def intersaction(la, lb):
    ans = LinkList()
    p = ans.head

    p1 = la.head.next
    p2 = lb.head.next

    while p1 is not None and p2 is not None:
        if p1.data == p2.data:
            p.next = p1
            p = p.next
            p1 = p1.next
            p2 = p2.next
        else:
            if p1.data < p2.data:
                p1 = p1.next
            else:
                p2 = p2.next
    return ans

6-4 集合差集

双指针法

def difference(la, lb):
    ans = LinkList()
    p = ans.head
    cnt = 0

    p1 = la.head.next
    p2 = lb.head.next

    while p1 is not None and p2 is not None:
        # print(f"now p1={p1.data} p2={p2.data}")
        if p2.data < p1.data:
            # print(f"jump {p2.data}")
            p2 = p2.next
        else:
            if p1.data == p2.data:
                # print(f"same:{p1.data}")
                p1 = p1.next
            else:
                # print(f"insert {p1.data}")
                p.next = p1
                p = p.next
                p1 = p1.next
                p.next = None
                cnt += 1
    while p1 is not None:
        # print(f"insert {p1.data}")
        p.next = p1
        p1 = p1.next
        p = p.next
        cnt += 1
    return ans, cnt

6-5 链表分解

这道题疑似题面有误，还需要将链表倒置。

• 可以在一开始就将la=inverse(la)完成倒置

• 也可以如下代码最后一行return inverse(b), inverse(c)

链表倒置的代码来自6-7，所以建议先完成6-7。

def inverse(la):
    p1 = la.head.next
    p2 = p1.next
    lb = LinkList()

    p1.next = None
    while p2 is not None:
        tmp = p2.next
        p2.next = p1
        p1 = p2
        p2 = tmp
    lb.head.next = p1
    return lb


def decompose(la):
    b = LinkList()
    c = LinkList()
    pb = b.head
    pc = c.head
    p = la.head.next

    while p is not None:
        if p.data > 0:
            pc.next = p
            pc = pc.next
            p = p.next
            pc.next = None
        elif p.data < 0:
            pb.next = p
            pb = pb.next
            p = p.next
            pb.next = None
        else:
            p = p.next

    return inverse(b), inverse(c)

6-6 链表最大值

比较简单

def max(la):
    p = la.head.next
    ans = p
    while p is not None:
        if p.data > ans.data:
            ans = p
        p = p.next
    return ans.data

6-7 链表逆置

def inverse(la):
    p1 = la.head.next
    p2 = p1.next
    lb = LinkList()

    p1.next = None
    while p2 is not None:
        tmp = p2.next
        p2.next = p1
        p1 = p2
        p2 = tmp
    lb.head.next = p1
    return lb

6-8 链表的条件删除

比较简单

def delete_min_max(la, mink, maxk):
    p = la.head.next
    last = la.head
    while p is not None:
        if p.data > mink and p.data < maxk:
            last.next = p.next
        else:
            last = last.next
        p = p.next
    return la

6-9 双循环链表节点换序

比较难，但是是上个学期的知识点（扩展）

注意多一格缩进

    def exchange(self, p):
        p1 = p.prior
        p0 = p1.prior
        p1.prior.next = p
        p.next.prior = p1
        p1.next = p.next
        p1.prior = p
        p.prior = p0
        p.next = p1

6-10 顺序表删除所有指定元素

不是链表题

按照题目的要求，需要控制时间复杂度和空间复杂度，所以不能使用judge里面的那些函数。（未测试能否使用、是否有时空检测）

def delete_item(a, item):
    tail = 0
    for p in range(0, a.length):
        if a.elem[p] == item:
            continue
        a.elem[tail] = a.elem[p]
        p += 1
        tail += 1
    a.length = tail
    return a

第三章

PTA编程题

很多题目都可以用一些非正确的方法过去，但是会有很多的漏洞。希望大家不要以过题为目的，而是真正理解并运用。

6-1 双栈

注意这道题需要提交完整代码。

class DblStack:
    def __init__(self,e): # 双栈初始化
        self.m=e
        self.V=[None]*self.m
        self.bot=[-1,self.m]
        self.top=[-1,self.m]
    def dbl_push(self, e, t): # 把元素 e 进栈
        if self.dbl_full():
            print("栈满")
            return
        if t==0:
            self.top[t] += 1
        else:
            self.top[t] -= 1
        # print(f"top[{t}]={self.top[t]}")
        self.V[ self.top[t] ]=e
    def dbl_pop(self, t): # 出栈
        if self.dbl_empty(t):
            print("栈空")
            return None
        ans=self.V[ self.top[t] ]
        self.V[ self.top[t] ]=None
        if t==0:
            self.top[t] -= 1
        else:
            self.top[t] += 1
        return ans
    def dbl_empty(self, stack_num):
        return self.top[stack_num] == self.bot[stack_num]
    def dbl_full(self):
        return self.top[0] + 1 == self.top[1]
    def show(self):
        for i in range(self.m):
            if self.V[i] is not None:
                print(self.V[i], end=' ')
        print()


if __name__ == '__main__':

    # 输入双栈容量c

    c = int(input())

    ds = DblStack(c)
    for i in range(c):
        j = i % 2
        print(i, end=' ')
        ds.dbl_push(i, j)
    print()

    ds.show()

    for i in range(c):
        j = i % 2
        print(ds.dbl_pop(j), end=' ')
    print()

6-2 回文判断

def is_palindrome(t):
    # 这题是要求用栈的，但是我偷懒了……
    half=len(t)//2
    for a in range(0,half+1):
        b=len(t)-a-1
        if t[a]!=t[b]:
            return False
    return True

6-3 键盘输入栈

def in_out_s(s,a):
    st=[]
    for x in a:
        if x==-1:
            if len(st)>0:
                print(f"出栈元素是 {st[-1]}")
                st.pop()
            else:
                print("栈空")
        else:
            st.append(x)
        if len(st)>max_size:
            print("栈满")
            return

6-4 计算后缀表达式的值

def calc(a,b,ch):
    if ch=='+':
        return a+b
    if ch=='-':
        return a-b
    if ch=='*':
        return a*b
    return a/b

def postfix(e):
    x=""
    element=[]
    for ch in e:
        if ch in "+-*/$ ":
            if len(x):
                element.append(x)
            element.append(ch)
            x=""
        else:
            x+=ch
        # print(element)

    for e in element:
        if e not in "0123456789+-*/$":
            element.remove(e)

    # print(element)

    # if element[-1]!='$':
    #     return 0

    stack=[]
    for x in element:
        if x is None:
            continue
        if x in ['+','-','*','/']:
            b=stack.pop()
            a=stack.pop()
            stack.append(calc(a,b,x))
            # print("push ", calc(a,b,x))
        elif x=='$':
            return stack.pop()
        else:
            stack.append(float(x))
            # print("push ",x)
    return stack.pop()

6-5 判断进出栈序列是否合法

def check(seq):
    sum=0
    for ch in seq:
        if ch == 'I':
            sum+=1
        else:
            sum-=1
        if sum<0:
            return False
    if sum!=0:
        return False
    return True

整个活

这个check函数的返回值只有True和False两种。而本题的数据点仅两个，很少。所以……随机返回值，然后多提交几次就过去了……

import random
import time
def check(seq):
 random.seed(time.time())
 return random.randint(0,2)

6-6 循环链表表示队列

class LinkQueue:
    def __init__(self): # ⽣成新结点作为头结点并初始化指针域和数据区域为 None，头指针 head 指向头结点
        self.head=LNode()
        self.head.data=None
        self.head.next=self.head
    def enqueue(self, e): # ⼊队
        p=LNode()
        p.data=e
        p.next=self.head.next
        self.head.next=p
        self.head=p

    def dequeue(self): # 出队
        if self.head.next == self.head:
            print("队列为空")
            return
        ans=self.head.next.next.data
        self.head.next.next=self.head.next.next.next
        return ans

    def empty(self):
        self.head.next=self.head

6-7 带标志的循环队列

class CirQueue:
    def __init__(self, max_volume=5):
        self.m=max_volume
        self.V=[None]*max_volume
        self.front=0
        self.rear=0
        self.tag=0
    def enqueue(self, e): # ⼊入队
        if self.tag==1:
            print("已满")
            return
        self.front+=1
        self.front%=self.m
        self.V[self.front]=e
        if self.rear==self.front:
            self.tag=1
    def dequeue(self): # 出队
        if self.front==self.rear:
            if self.tag==0:
                print("空")
                return
            else:
                self.tag=0
        self.rear+=1
        self.rear%=self.m
        return self.V[self.rear]

6-8 双向循环队列

class CirQueue:

    def __init__(self, max_volume=5):
        self.m = max_volume
        self.V = [None] * max_volume
        self.front = 0
        self.rear = 0
        self.tag = 0
    def enqueue(self, e): # 从队尾入队
        if self.tag==1:
            print("已满")
            return
        self.V[self.rear]=e
        self.rear+=self.m-1
        self.rear%=self.m
    def dequeue(self): # 从队头出队
        if self.front==self.rear:
            if self.tag==0:
                print("空")
                return
            else:
                self.tag=0
        ans=self.V[self.front]
        self.front+=self.m-1
        self.front%=self.m
        return ans
    def enqueue_from_head(self, e):
        if self.tag==1:
            print("已满")
            return
        self.front+=1
        self.front%=self.m
        self.V[self.front]=e
        if self.rear==self.front:
            self.tag=1
    def dequeue_from_tail(self):
        if self.front==self.rear:
            if self.tag==0:
                print("空")
                return
            else:
                self.tag=0
        self.rear+=1
        self.rear%=self.m
        return self.V[self.rear]

6-9 Ackermann函数计算

这个非递归的方式计算有点意思呢

def ack(m, n): # ackermann 函数递归
    if m==0:
        return n+1
    if n==0:
        return ack(m-1,1)
    return ack(m-1,ack(m,n-1))


def ackermann(m, n): # ackermann 函数非递归
    ans=[]
    M=m+10
    N=n+10
    for i in range(M+1):
        ans.append([0]*(N+1))
    for y in range(N):
        ans[0][y]=y+1
    for x in range(1,m+1):
        ans[x][0] = ans[x - 1][1]
        for y in range(1,N):
            ans[x][y]=ans[x-1][ans[x][y-1]]
    return ans[m][n]

6-10 单链表的递归运算

def max_integer(p):
    if p.next is None:
        return p.data
    return max(p.data,max_integer(p.next))
def node_number(p):
    if p.next is None:
        return 1
    return node_number(p.next)+1
def sum_integer(p):
    if p.next is None:
        return p.data
    return p.data+sum_integer(p.next)
def avg(p):
    return sum_integer(p)/node_number(p)

第四章

PTA编程题

6-1 字符统计

这次第一题太逆天了。

首先看到输出样例中，“字⺟字符 A 的个数= 0”的“⺟”不是“母”。

该字符的Unicode编码为（\u2e9f）属于汉字部首的范围。具体来说，它是一个部首，通常与汉字的构造和意义相关联。在Unicode中，这个字符位于“CJK 部首”块中，主要用于表示与汉字相关的语义和结构。

第二个需要注意的点是不区分字母的大小写，一律按照大写统计。

第三个需要注意的点是，输入的字符串中可能不止有数字和字母，还有其他的字符。如果你没有通过第二个测试点，则考虑这个问题。

def count(s):
    root="0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
    s=s.upper()
    ans=[0]*len(root)
    for ch in s:
        if ch.isdigit():
            ans[int(ch)]+=1
        if ch.isalpha():
            ans[ord(ch)-ord('A')+10]+=1
    # print(ans)
    for x in range(len(root)):
        if root[x].isdigit():
            out="数字"
        else:
            out="字⺟字符"
        print(f"{out} {root[x]} 的个数= {ans[x]}")

这个“⺟”太邪恶了吧！

6-2 字符串逆序存储

题目要求不“另外串储存空间”，好怪啊，是说不另外使用储存空间吗？但是python的字符串是不可修改的，切片等很多字符串操作看上去没有使用额外空间，但是其实在其内部是使用了的啊。

def inverse(ch):
    if len(ch)==1:
        return ch
    return ch[-1]+inverse(ch[:-1])

6-3 自定义字符串插入函数

这题目更邪恶了，给的接口后面的冒号是中文的……

函数结构定义：

# 将字符串t插入到字符串s中，插入位置为pos

def  insert(s, t,  pos)：

这里最后的冒号是中文的……

def insert(s, t,  pos):
    if 1 <=pos<=len(s):
        return s[0:pos-1]+t+s[pos-1:]
    return False

6-4 字符串格式化-Python

def format(s1, s2, s3, n):
    s1=s1.strip()
    if len(s1)==0:
        return 1
    if len(s1)<n:
        return 2
    s2.append(s1[:n])
    s3.append(s1[n:])
    return 0

6-5 判断数组中是否有相同元素

本来想整点花活的，比如用快排或者平衡树压一下时间复杂度到 \(O(mn\log mn)\) 的。但是还是算了吧，不花时间整活了。

这题也有点邪恶了。题目需要“判断二维数组中是否有相同的元素”，但是最后输出yes或no回答的问题是“判断二维数组中所有数字是否都不相同”；需要些的接口函数的名字是is_equal，但是却需要在没有相同数字的时候返回True……

def is_equal(a, m, n):
    judge=[]
    for i in range(m):
        for j in range(n):
            if a[i][j] in judge:
                return 0
            judge.append(a[i][j])
    return 1

如果说以前的题目是不小心的，这次这6道题绝对是故意的了吧……？有意思吗这题目……

算了，那只能整个活回敬一下了！用splay把时间复杂度降下来（

class Node:
    def __init__(self, val):
        self.val = val
        self.cnt = 1
        self.size = 1
        self.left = None
        self.right = None
        self.parent = None

class Splay:
    def __init__(self):
        self.root = None

    def update(self, node):
        if node:
            node.size = (node.left.size if node.left else 0) + (node.right.size if node.right else 0) + node.cnt

    def rotate(self, x):
        y = x.parent
        z = y.parent
        if y.left == x:
            y.left = x.right
            if x.right:
                x.right.parent = y
            x.right = y
        else:
            y.right = x.left
            if x.left:
                x.left.parent = y
            x.left = y
        x.parent = z
        y.parent = x
        if z:
            if z.left == y:
                z.left = x
            else:
                z.right = x
        self.update(y)
        self.update(x)

    def splay(self, x):
        while x.parent:
            y = x.parent
            if y.parent:
                if (y.left == x) == (y.parent.left == y):
                    self.rotate(y)
                else:
                    self.rotate(x)
            self.rotate(x)
        self.root = x

    def find(self, val):
        x = self.root
        while x:
            if x.val == val:
                self.splay(x)
                return x
            elif val < x.val:
                if not x.left:
                    break
                x = x.left
            else:
                if not x.right:
                    break
                x = x.right
        if x:
            self.splay(x)
        return x

    def insert(self, val):
        if not self.root:
            self.root = Node(val)
            return
        x = self.find(val)
        if x.val == val:
            x.cnt += 1
            x.size += 1
            return
        new = Node(val)
        if val < x.val:
            new.left = x.left
            if x.left:
                x.left.parent = new
            x.left = new
            new.parent = x
        else:
            new.right = x.right
            if x.right:
                x.right.parent = new
            x.right = new
            new.parent = x
        self.splay(new)

    def delete(self, val):
        x = self.find(val)
        if x.val != val:
            return
        if x.cnt > 1:
            x.cnt -= 1
            x.size -= 1
            return
        if not x.left and not x.right:
            self.root = None
        elif not x.left:
            self.root = x.right
            x.right.parent = None
        elif not x.right:
            self.root = x.left
            x.left.parent = None
        else:
            y = x.left
            while y.right:
                y = y.right
            self.splay(y)
            y.right = x.right
            x.right.parent = y
            self.root = y
            y.parent = None
        self.update(self.root)

    def rank(self, val):
        x = self.find(val)
        return (x.left.size if x.left else 0) + 1

    def kth(self, k):
        x = self.root
        while True:
            left_size = x.left.size if x.left else 0
            if left_size >= k:
                x = x.left
            elif left_size + x.cnt < k:
                k -= left_size + x.cnt
                x = x.right
            else:
                self.splay(x)
                return x.val

    def predecessor(self, val):
        x = self.find(val)
        if x.val < val:
            return x.val
        if x.left:
            x = x.left
            while x.right:
                x = x.right
            return x.val
        while x.parent and x.parent.left == x:
            x = x.parent
        return x.parent.val if x.parent else None

    def successor(self, val):
        x = self.find(val)
        if x.val > val:
            return x.val
        if x.right:
            x = x.right
            while x.left:
                x = x.left
            return x.val
        while x.parent and x.parent.right == x:
            x = x.parent
        return x.parent.val if x.parent else None
tree = Splay()



def cmain():
    n = int(input())
    tree = Splay()
    for _ in range(n):
        op, x = map(int, input().split())
        if op == 1:
            tree.insert(x)
        elif op == 2:
            tree.delete(x)
        elif op == 3:
            print(tree.rank(x))
        elif op == 4:
            print(tree.kth(x))
        elif op == 5:
            print(tree.predecessor(x))
        elif op == 6:
            print(tree.successor(x))


def is_equal(a, m, n):
    for row in a:
        for x in row:
            tree.insert(x)
            if tree.find(x).cnt>1:
                return 0
    return 1

6-6 正负分类

太逆天了……但是也合情合理。

这堂堂PTA，居然不能放一个spj上去？

初见这道题第一反应当然是双指针，最短的时间复杂度而且还不占额外空间。

但是样例输出着实让我懵了一下：

in:

5

1 -1 2 -2 3

out:

1 3 2 -2 -1

就算限定 \(O(n)\) 的时间复杂度且不能使用额外空间，就算必须使用双指针法，方法也有很多的呀。比如下面给出一种双指针：

def partition(A, n):
    i=0
    for j in range(n):
        if A[j]>0:
            A[i],A[j]=A[j],A[i]
            i+=1
    return A

其样例输出为：

1 2 3 -2 -1

我的第一种思路便是如此：双指针都从左边出发；右指针负责找到正数，左指针负责指向下一个正数应该摆放的位置。

这样输出的答案也是符合题意的，但是不符合这题的答案。有点无语。

下面是“标准”答案：

def partition(A, n):
    i=0
    j=n-1
    while i<j:
        if A[i]<0 and A[j]>0:
            A[i],A[j]=A[j],A[i]
        else:
            if A[i]>0:
                i+=1
            else:
                j-=1
    return A

其实说吧，这种方法可能是想防止有人用sort或者额外数组等简单粗暴的方法通过这道题吧，所以才出此下策。但是这也太恶心人了吧，算是最懒最不严谨的一种做法了。

首先为了规范题目评测标准，应该使用spj（以防你不知道Special Judge是什么），即判定输出是符合题目要求的（输出数据为输入数据的一个排列，且前半段为正数后半段为负数），若符合则通过。

其次，为了防止有人用错误的时间复杂度通过，应该扩大数据量，使得在时间限制内无法允许排序等 \(O(n\log n)\) 的算法通过。

这里举一个 \(O(n\log n)\) 的例子：

def partition(A, n):
    b=sorted(A,reverse=True)
    A.clear()
    A.extend(b)

最后，可以使用静态检查或者动态检查以判断是否申明了多余的空间，淘汰掉如下面这样的算法：

def partition(A, n):
    b=[]
    c=[]
    for x in A:
        if x>0:
            b.append(x)
        else:
            c.append(x)
    A.clear()
    A.extend(b)
    A.extend(c)

说完上面这些，我发觉，这些可能对于出题者来说还是太难了吧。所以1 3 2 -2 -1 ，似乎也能理解了。可能有点想法，想要把非标准做法统统砍掉；但是有没有考虑到有多种“标准”做法呢？

第五章

PTA编程题

6-1 统计二叉树叶子结点数目

def leaf_node(root):
    if root.data==None:
        return 0
    if root.lchild.data==None and root.rchild.data==None:
        return 1
    return leaf_node(root.lchild)+leaf_node(root.rchild)

6-2 判断两棵树是否相等

• 当前节点的存在情况是否一致
• 当前节点的值是否一致
• 当前节点是否可能有左右儿子？有的话递归左右儿子

def cmp_tree(tree1, tree2):
    if (tree1==None) != (tree2==None):
        return 0
    if tree1==None:
        return 1
    if tree1.data!=tree2.data:
        return 0
    return cmp_tree(tree1.lchild,tree2.lchild) and cmp_tree(tree1.rchild,tree2.rchild)

6-3 交换二叉树结点的左右孩子

def change_lr(root):
    if root.data==None:
        return
    root.lchild,root.rchild=root.rchild,root.lchild
    change_lr(root.lchild)
    change_lr(root.rchild)

6-4 二叉树的双序遍历

# 注意缩进
    def double_traverse(self):
        if self.data==None:
            return
        print(self.data,end=' ')
        self.lchild.double_traverse()
        print(self.data, end=' ')
        self.rchild.double_traverse()

6-5 计算二叉树最大宽度

# 注意缩进
    def width(self):
        ans=0
        q2=SqQueue()
        q2.en_queue(self)
        while not q2.queue_empty():
            ans=max(ans,len(q2))
            q1=q2
            q2=SqQueue()
            while not q1.queue_empty():
                x=q1.de_queue()
                if x.lchild.data!=None:
                    q2.en_queue(x.lchild)
                if x.rchild.data!=None:
                    q2.en_queue(x.rchild)
        return ans

6-6 按层统计二叉树度为1的结点个数

整活（防抄袭？

# 注意缩进
    def level(self):
        return ((self.lchild.data==None)+(self.rchild.data==None)==1)+(self.lchild.level() if self.lchild.data!=None else 0)+(self.rchild.level() if self.rchild.data!=None else 0)

给段ai解释吧，偷懒了

下面是对 level 方法的详细解释：

def level(self):
 return ((self.lchild.data==None)+(self.rchild.data==None)==1) + \
        (self.lchild.level() if self.lchild.data!=None else 0) + \
        (self.rchild.level() if self.rchild.data!=None else 0)

逻辑分析

1. 度为1的节点的判断：

• self.lchild.data == None：检查左子节点是否为空。
• self.rchild.data == None：检查右子节点是否为空。
• ((self.lchild.data==None) + (self.rchild.data==None) == 1)：
  • 这部分的逻辑是将上述两个条件的布尔值（True 为 1，False 为 0）相加，如果相加的结果等于 1，说明只有一个子节点存在，即该节点的度为1。
  • 如果该节点的度为1，返回 True（即 1），否则返回 False（即 0）。

2. 递归统计左子树的度为1的节点：

• (self.lchild.level() if self.lchild.data != None else 0)：
  • 如果左子节点存在（self.lchild.data != None），则递归调用左子节点的 level 方法，统计左子树中度为1的节点个数。
  • 如果左子节点为空，返回 0。

3. 递归统计右子树的度为1的节点：

• (self.rchild.level() if self.rchild.data != None else 0)：
  • 同样地，如果右子节点存在，则递归调用右子节点的 level 方法，统计右子树中度为1的节点个数。
  • 如果右子节点为空，返回 0。

总结

这段代码通过递归的方式统计当前节点及其子树中度为1的节点个数。最终返回值是三个部分的和：

• 当前节点是否度为1（1或0）。
• 左子树中度为1的节点个数。
• 右子树中度为1的节点个数。

这样，level 方法能够有效地计算整个二叉树中度为1的节点总数。

6-7 二叉树的最长路径

被恶心到啦。

做第五章之前看了一眼排行榜，发现大家都没过这道题呢，就怀疑这道题有时又什么猫腻吧。

但是也没那么严重，没有上个章节的题目，全是坑坑洼洼的啦~

这次需要注意的是：题目给的存储路径的数据结构是栈，主函数输出栈的时候，是从栈顶开始输出的；但是观察样例可以发现，这棵树长这样：

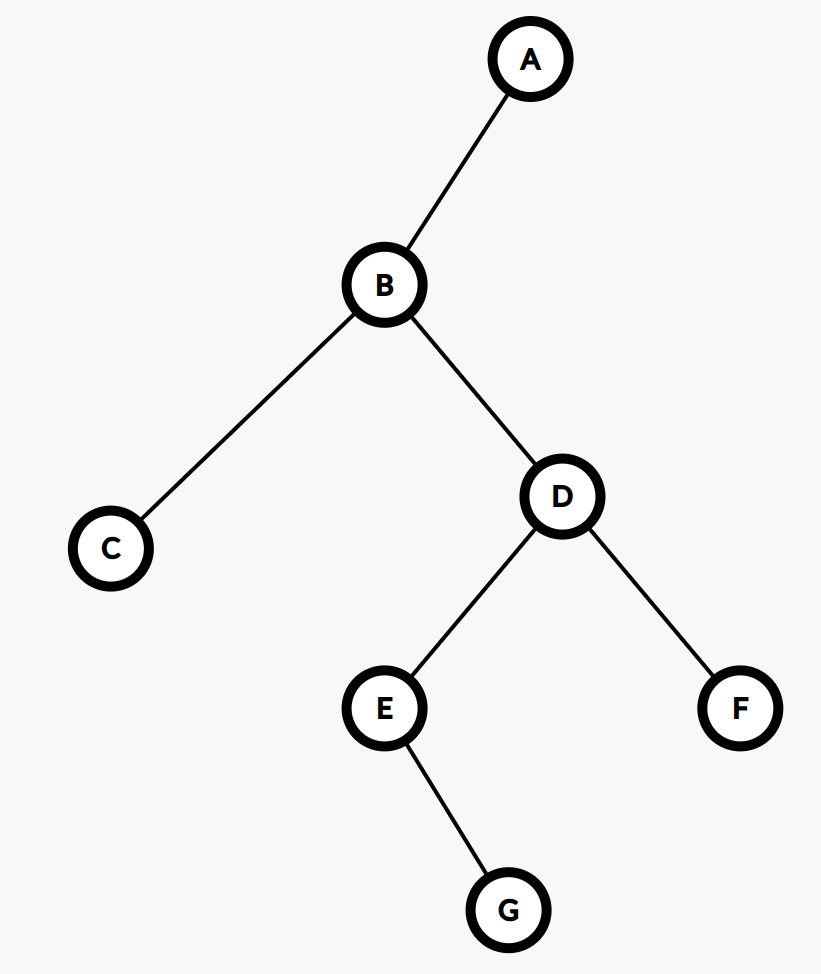
但是其最长路径却是：

最⻓路径为：
G E D B A 

也就是说，是从叶子节点向根节点依次输出的。

但是由于题目给的数据结构是栈，所以就需要先将根节点入栈。

如果说像我一样偷懒，写了一个递归方式的，那么肯定是叶子节点先入栈的，输出的结果就正好反过来了。

下面给一份错误示例代码：

# 注意缩进
    def longest_path(self):
        q=SqStack()
        if self.data==None:
            return len(q),q
        _,ans1=self.lchild.longest_path()
        _,ans2=self.rchild.longest_path()
        if len(ans1)>=len(ans2):
            ans=ans1
        else:
            ans=ans2

        ans.push(self)

        return len(ans),ans

那么怎么办呢？

两种解决方法：

1. 每次push进入的节点，push到栈底。需要先把栈内元素全部取出、放入当前元素、把之前取出的元素重新放回。

# 注意缩进
    def longest_path(self):
        q=SqStack()
        if self.data==None:
            return len(q),q
        _,ans1=self.lchild.longest_path()
        _,ans2=self.rchild.longest_path()
        if len(ans1)>=len(ans2):
            ans=ans1
        else:
            ans=ans2
        temp=SqStack()
        while not ans.stack_empty():
            temp.push(ans.pop())

        ans.push(self)

        while not temp.stack_empty():
            ans.push(temp.pop())

        return len(ans),ans

2. 题目需要的函数接口longest_path(self)调用另一个递归函数用于得到最长路径，而longest_path(self)实现将得到的最长路径反转。

# 注意缩进
    def my_longest_path(self):
        q=SqStack()
        if self.data==None:
            return len(q),q
        _,ans1=self.lchild.my_longest_path()
        _,ans2=self.rchild.my_longest_path()
        if len(ans1)>=len(ans2):
            ans=ans1
        else:
            ans=ans2

        ans.push(self)

        return len(ans),ans

    def longest_path(self):
        _,ans=self.my_longest_path()
        temp=SqStack()
        while not ans.stack_empty():
            temp.push(ans.pop())
        return _,temp

3. 也可以使用分层遍历的方法，再此不作赘述了。方法多种多样。

只是说呢，没有想到，上一章那么恶心坑坑洼洼，大家都做出来了；这一章咋被这区区一个反转栈困住了呢？

6-8 输出二叉树所有叶子到根的路径

也有类似上述的问题， 希望我用list存路径，但是却希望我从叶子节点向根节点输出……

还好，比栈好处理一点，reversed一下就好了。

另外注意，二叉树有那么多的jie点，比如更节电，叶子洁点，左姐点，右截点，父亲羯点，有好多好多的jie点呢！我真的不知道应该叫做节点还是结点……不如，我们叫他们都叫node吧！

我是真没注意这个字。

百度百科上“结”多；维基百科中的二叉树前半部分多用“节点”（63次），后半部分多用“结点”（76次）。

我一般习惯用“节”。“节”的笔划更少，并且我个人认为“节点”更适合，因为“节点”更像是树上的两条边之间的“节点”；而“结点”，“结果”，仿佛只存在于树的边缘（叶子节点）一样呢。

# 注意缩进
    def all_path(self, path, pathlen):
        path.append(self.data)
        if self.lchild.data==None and self.rchild.data==None:
            print(f"{self.data} 到根结点路径:",end=' ')
            for x in reversed(path):
                print(x,end=' ')
            print()

        if self.lchild.data!=None:
            self.lchild.all_path(path,pathlen+1)
        if self.rchild.data!=None:
            self.rchild.all_path(path,pathlen+1)
        path.pop()

第六章

PTA编程题

6-1 图的基本操作（邻接矩阵）

说在前面

这道题的标准程序出错了，导致第二个样例也错误了，所以很多同学（不是很多，是所有）都被卡住了。

不知道后续老师会不会修复这个问题。要是没修复，就直接提交下面的错误的标程就好了（（（

所以，这次先来看看标程吧！

##注意缩进
    ##请在这里填写答案
    def insert_vex(self, v):
        # 在以邻接矩阵形式存储的⽆向图 g 上插⼊顶点 v
        if self.vexnum + 1 > 100:
            return 'INFEASIBLE' # 判断插⼊操作是否合法
        self.vexnum = self.vexnum + 1 # 增加图的顶点数量
        self.vexs.append(v) # 将新顶点 v 存⼊顶点表
        for k in range(0, self.vexnum): # 邻接矩阵相应位置的元素置为 1
            self.arcs[self.vexnum-1][k] = INF
            self.arcs[k][self.vexnum-1] = INF
        return 'OK'

    def delete_vex(self, v):
        # 在以邻接矩阵形式存储的⽆向图 g 上删除顶点 v
        n = self.vexnum
        m = self.locate_vex(v)
        if m < 0:
            return 'ERROR' # 判断删除操作是否合法，即 v 是否在 g 中
        for i in range(0, n): # 将边的关系随之交换
            for j in range(0, n):
                if i > m and j > m:
                    self.arcs[i - 1][j - 1] = self.arcs[i][j]
                else:
                    if i > m:
                        self.arcs[i - 1][j] = self.arcs[i][j]

                    else:
                        if j > m:
                            self.arcs[i][j - 1] = self.arcs[i][j]
        for m in range(m, n - m - 1): # 将待删除顶点交换到最后⼀个顶点
            t = self.vexs[m]
            self.vexs[m] = self.vexs[m + 1]
            self.vexs[m + 1] = t
        self.vexnum = self.vexnum - 1 # 顶点总数减１
        return 'OK'

    def insert_arc(self, v, w):
        # 在以邻接矩阵形式存储的⽆向图 g 上插⼊边(v,w)
        i = self.locate_vex(v)
        j = self.locate_vex(w)
        if i < 0: # 判断插⼊位置是否合法
            return 'ERROR'
        if j < 0: # 判断插⼊位置是否合法
            return 'ERROR'
        self.arcs[i][j] = self.arcs[j][i] = 1 # 在邻接矩阵上增加对应的边
        self.arcnum = self.arcnum + 1 # 边数加１
        return 'OK'

    def delete_arc(self, v, w):
        # 在以邻接矩阵形式存储的⽆向图 g 上删除边(v,w)
        i = self.locate_vex(v)
        j = self.locate_vex(w)
        if i < 0: # 判断插⼊位置是否合法
            return 'ERROR'
        if j < 0: # 判断插⼊位置是否合法
            return 'ERROR'
        self.arcs[i][j] = self.arcs[j][i] = INF # 在邻接矩阵上删除边
        self.arcnum = self.arcnum - 1 # 边数减１
        return 'OK'
    def show(self):
        for i in range(0, self.vexnum):
            for j in range(0, self.vexnum):
                if j != self.vexnum-1:
                    if(self.arcs[i][j] < INF):
                        print(self.arcs[i][j], end="\t")
                    else:
                        print("∞\t", end="")
                else:
                    if (self.arcs[i][j] < INF):
                        print(self.arcs[i][j])
                    else:
                        print("∞")

先说一下标程的两个错误：

对于增加和删除操作，并没有修改arcs邻接矩阵的大小

观察前两个函数可以发现，当新增/删除一个点的时候，其并不会修改arcs数组的大小，只是修改而已。

比如说删除的时候，只是将该行该列挪到了最后行一列：

for i in range(0, n): # 将边的关系随之交换
    for j in range(0, n):
        if i > m and j > m:
            self.arcs[i - 1][j - 1] = self.arcs[i][j]
        else:
            if i > m:
                self.arcs[i - 1][j] = self.arcs[i][j]

            else:
                if j > m:
                    self.arcs[i][j - 1] = self.arcs[i][j]
     

以及新增的时候，只是把vexs加了一个，然后直接使用对应的arcs邻接矩阵的位置：

self.vexnum = self.vexnum + 1 # 增加图的顶点数量
self.vexs.append(v) # 将新顶点 v 存⼊顶点表
for k in range(0, self.vexnum): # 邻接矩阵相应位置的元素置为 1
    self.arcs[self.vexnum-1][k] = INF
    self.arcs[k][self.vexnum-1] = INF

整个过程，都没有修改arcs的大小。arcs的大小在创建图（函数create_udn中）的时候就确定，之后再也没有修改过了。

self.arcs = [[INF for i in range(self.vexnum)] for i in range(self.vexnum)]  # 初始化邻接矩阵，边的权值均置为无穷大

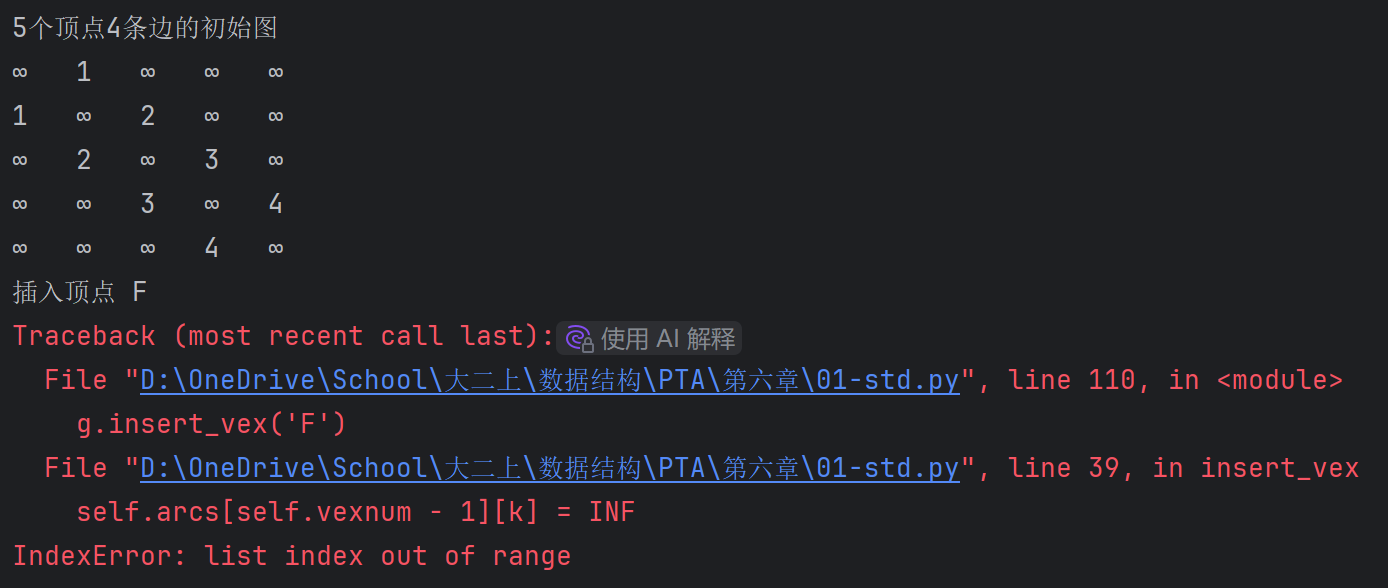
这会导致，如果图创建的时候有ABCDE五个节点，之后直接使用insert_vex，会报错，arcs数组访问越界。

删除节点时，未能成功将被删除的节点挪到vexnum的最后末尾

在函数delete_vex当中，期望将被删除的点挪到当前有效点位列表（vexs的[0,n）的末尾，但是：

for m in range(m, n - m - 1):  # 将待删除顶点交换到最后⼀个顶点
    print("swap", m, m + 1)
    t = self.vexs[m]
    self.vexs[m] = self.vexs[m + 1]
    self.vexs[m + 1] = t
self.vexnum = self.vexnum - 1  # 顶点总数减１

但是，这个for循环枚举的是 \(now\in[m,n-m-1)\) ，也就是说，只会将位于m、准备要被删除的这个元素，挪到下标为n-m-1的位置上？

这个错误也太严重了吧。随便构造数据卡掉这玩意：

1. 首先输入一个5个点的图。为了偷懒，就拿题目的样例吧。

   5
   4
   A
   B
   C
   D
   E
   A
   B
   1
   B
   C
   2
   C
   D
   3
   D
   E
   4
   

   结果如下：

   5个顶点4条边的初始图
   ∞	1	∞	∞	∞
   1	∞	2	∞	∞
   ∞	2	∞	3	∞
   ∞	∞	3	∞	4
   ∞	∞	∞	4	∞
   

2. 然后把B点删了

   # 删除顶点 'B'
   print('删除顶点 B')
   g.delete_vex('B')
   g.show()
   

   结果如下：

   删除顶点 B
   ∞	∞	∞	∞
   ∞	∞	3	∞
   ∞	3	∞	4
   ∞	∞	4	∞
   

   这时候，表面看上去一切正常。这时候，我们期望B会被移到ABCDE的最后一个，也就是变成ACDE(B)。但是其实，range(m,n-1)也就是range(1,5-1-1)=range(1,3)={1,2}所以循环只会进行两次，会将ABCDE变成ACDBE。然后，vexnum-=1，导致真正被删除的是E。

3. 那么想要hack，只需要连接AE

   # 连接 AE
   print('连接 AE')
   g.insert_arc('A', 'E')
   g.show()
   

   

   然后就报错咯，这里是因为找不到E，导致locate_vex('E')返回了个NoneType。

4. 也可以尝试连接AB

   这时候看似已经删除了B，其实并没有。locate_vex('B')的结果应该是3。尝试连接AB：

   print("locate_vex(B)=", g.locate_vex('B'))
   # 连接 AB
   print('连接 AB')
   g.insert_arc('A', 'B')
   g.show()
   

   输出如下：

   locate_vex(B)= 3
   连接 AB
   ∞	∞	∞	1     <-连接到了这里了啊哈哈
   ∞	∞	3	∞
   ∞	3	∞	4
   1	∞	4	∞
   ↑还有这里
   

   发现，B确实存在，且其下标是3。连接AB，也“成功”连接上了，哈哈哈。

下面给出我的（无法通过第二个测试点）的代码

# 注意缩进
    def insert_vex(self, v):
        if self.vexnum + 1 > 100:
            return 'INFEASIBLE' # 判断插⼊操作是否合法
        if self.locate_vex(v):
            print('顶点已存在')
            return
        self.vexs.append(v)
        for i in range(0, self.vexnum):
            self.arcs[i].append(INF)
        self.vexnum+=1
        self.arcs.append([INF for i in range(self.vexnum)])

    def delete_vex(self, v):
        index=self.locate_vex(v)
        for i in range(0, self.vexnum):
            self.arcs[i].pop(index)
        self.arcs.pop(index)
        self.vexs.pop(index)
        self.vexnum-=1

    def insert_arc(self, v, w,weight=1):
        v = self.locate_vex(v)
        w = self.locate_vex(w)
        if v == -1 or w == -1:
            return
        self.arcs[v][w]=self.arcs[w][v]=weight
        self.arcnum+=1

    def delete_arc(self, v, w):
        v = self.locate_vex(v)
        w = self.locate_vex(w)
        if v == -1 or w == -1:
            return
        self.arcs[v][w]=self.arcs[w][v]=INF
        self.arcnum-=1

6-2 图的基本操作（邻接表）

这题我觉得有问题但是测试点没有遇到，所以先放上我的答案。

# 注意缩进
    def insert_vex(self, v):
        self.vertices.append(VNode(v))
        self.vexnum += 1

    def delete_A_B(self, v, w):
        # print("Deleting edge " + str(v) + "->" + str(w))
        p = self.vertices[v].firstarc
        if p is not None:
            if p.adjvex == w:  # If the first arc is the one to delete
                self.vertices[v].firstarc = p.nextarc
            else:
                q = p
                p = p.nextarc
                while p is not None:
                    if p.adjvex == w:
                        q.nextarc = p.nextarc
                        break
                    q = p
                    p = p.nextarc

    def delete_vex(self, v):
        v=self.locate_vex(v)
        # print("Deleting vertex " + str(v))
        p = self.vertices[v].firstarc
        while p is not None:
            x=p.adjvex
            # delete x -> v
            self.delete_A_B(v, x)
            self.delete_A_B(x, v)


            p = p.nextarc

        self.vertices[v].firstarc=None
        self.vertices.pop(v)
        self.vexnum -= 1


    def insert_arc(self, v, w):
        v=self.locate_vex(v)
        w=self.locate_vex(w)
        p1 = ArcNode()
        p2 = ArcNode()
        p1.adjvex = w
        p1.nextarc = self.vertices[v].firstarc
        self.vertices[v].firstarc = p1
        p2.adjvex = v
        p2.nextarc = self.vertices[w].firstarc
        self.vertices[w].firstarc = p2
        self.arcnum += 1



    def delete_arc(self, v, w):
        v=self.locate_vex(v)
        w=self.locate_vex(w)
        # Delete v->w
        self.delete_A_B(v, w)
        # Delete w->v
        self.delete_A_B(w, v)

好抽象。不想再对题目进行评价了。

在第36行，我使用了self.vertices.pop(v)，直接从veretices这个列表中删除了v这个节点。假如原来是ABCDE，执行g.delete_vex('C')，列表就变成了ABDE，这样后两个点就会和其下标错位：如果使用locate_vex('D')，得到的结果将会是3，但是此时如果之前存在边AD，在A的邻接表vertices[locate_vex('A')].firstarc中，该边的终点仍然是4（即原来的locate_vex('D')）吧？

再给一个具体的例子：

class ArcNode:  # 边结点
    def __init__(self):
        self.adjvex = 0  # 该边所指向的顶点的位置
        self.nextarc = None  # 指向下一条边的指针
        self.info = None  # 和边相关的信息


class VNode:  # 顶点信息
    def __init__(self, data):
        self.data = data  # 顶点信息
        self.firstarc = None  # 指向第一条依附该顶点的边的指针


class ALGraph:  # 邻接表
    def __init__(self):
        self.vertices = []
        self.vexnum = 0  # 图当前的顶点数
        self.arcnum = 0  # 图当前的边数

    def locate_vex(self, data):
        # 定位顶点在顶点数组中的下标
        for i in range(0, self.vexnum):
            if self.vertices[i].data == data:
                return i

    def create_udg(self):
        # 采用邻接表表示法，创建无向图
        self.vexnum = int(input())  # 输入总顶点数
        self.arcnum = int(input())  # 输入总边数
        for i in range(0, self.vexnum):  # 输入各点，构造表头结点表
            vdata = input()  # 输入顶点值
            vertex = VNode(vdata)
            self.vertices.append(vertex)
        for k in range(0, self.arcnum):  # 输入各边，构造邻接表
            v1 = input()
            v2 = input()  # 输入一条边依附的两个顶点
            i = self.locate_vex(v1)
            j = self.locate_vex(v2)  # 确定v1和v2在self中位置，即顶点在self.vertices中的序号
            p1 = ArcNode()  # 生成一个新的边结点p1
            p1.adjvex = j  # 邻接点序号为j
            p1.nextarc = self.vertices[i].firstarc
            self.vertices[i].firstarc = p1  # 将新结点p1插入顶点v1的边表头部
            p2 = ArcNode()  # 生成另一个对称的新的边结点p2
            p2.adjvex = i  # 邻接点序号为i
            p2.nextarc = self.vertices[j].firstarc
            self.vertices[j].firstarc = p2  # 将新结点p1插入顶点v1的边表头部

# 注意缩进
    def insert_vex(self, v):
        self.vertices.append(VNode(v))
        self.vexnum += 1

    def delete_A_B(self, v, w):
        # print("Deleting edge " + str(v) + "->" + str(w))
        p = self.vertices[v].firstarc
        if p is not None:
            if p.adjvex == w:  # If the first arc is the one to delete
                self.vertices[v].firstarc = p.nextarc
            else:
                q = p
                p = p.nextarc
                while p is not None:
                    if p.adjvex == w:
                        q.nextarc = p.nextarc
                        break
                    q = p
                    p = p.nextarc

    def delete_vex(self, v):
        v=self.locate_vex(v)
        # print("Deleting vertex " + str(v))
        p = self.vertices[v].firstarc
        while p is not None:
            x=p.adjvex
            # delete x -> v
            self.delete_A_B(v, x)
            self.delete_A_B(x, v)


            p = p.nextarc

        self.vertices[v].firstarc=None
        self.vertices.pop(v)
        self.vexnum -= 1


    def insert_arc(self, v, w):
        v=self.locate_vex(v)
        w=self.locate_vex(w)
        p1 = ArcNode()
        p2 = ArcNode()
        p1.adjvex = w
        p1.nextarc = self.vertices[v].firstarc
        self.vertices[v].firstarc = p1
        p2.adjvex = v
        p2.nextarc = self.vertices[w].firstarc
        self.vertices[w].firstarc = p2
        self.arcnum += 1





    def delete_arc(self, v, w):
        v=self.locate_vex(v)
        w=self.locate_vex(w)
        # Delete v->w
        self.delete_A_B(v, w)
        # Delete w->v
        self.delete_A_B(w, v)

    def show(self):
        for i in range(0, self.vexnum):
            t = self.vertices[i]
            p = t.firstarc
            if p is None:
                print(self.vertices[i].data)
            else:
                print(t.data, end="")
                while p is not None:
                    print("->", end="")
                    print(p.adjvex, end="")
                    p = p.nextarc
                print()


if __name__ == '__main__':
    g = ALGraph()
    g.create_udg()
    print(str(g.vexnum) + '个顶点' + str(g.arcnum) + '条边的初始图')
    g.show()
    print('增加边AE')
    g.insert_arc('A','E')
    g.show()
    g.delete_vex('C')
    print('删除顶点C')
    g.show()
    g.insert_arc('A','D')
    print('增加边AD')
    g.show()
    g.insert_vex('C')
    print('增加顶点C')
    g.show()

输入：

5
4
A
B
C
D
E
A
B
B
C
C
D
D
E

首先，输入的图是：

5个顶点4条边的初始图
A->1
B->2->0
C->3->1
D->4->2
E->3

在主函数中，首先执行连边AE：

增加边AE
A->4->1
B->2->0
C->3->1
D->4->2
E->0->3

可以看到，A后多了一个4，E后也多了一个0。

接着执行删除点C：

删除顶点C
A->4->1
B->0
D->4
E->0->3

发现，C没了，但是各个点的出边数字并没有变化。

那么这时候，在执行连接AD：

增加边AD
A->2->4->1
B->0
D->0->4
E->0->3

发现D后面确实多了一个0；A后面多了一个2——等等，2是谁？是D吗？还是那个已经被删除的C？这里就出现问题了：如果D=2，那么上面数字中的4又是谁呢？E？如果E=4，那么D应该是3才对。

再然后，尝试增加点C：

增加顶点C
A->2->4->1
B->0
D->0->4
E->0->3
C

会将其增加到C=4。但是这里已经有单向边A->4,D->4了……

总之就是很混乱。这种混乱的根本来源，是vertices。这个数组基于下标进行储存，但是删除某个点的时候，会导致该点之后的节点的下标发生变化；而此时，邻接表中存储的出边终点下标并没有变化……

我不知道这算是我写的函数的漏洞，还是算是题目没有考虑到这种情况？可以根据上述混乱产生的原理修复该漏洞。但是，这样会比较麻烦；而且我现在这样居然能通过两个测试点……不知道是测试点太弱了导致没有检测出该漏洞，还是测试点的答案也是如此？

6-3 深度优先遍历-非递归-邻接表

这题，先看看样例：

5个顶点6条边的初始图
A->2->1
B->4->3->0
C->4->3->0
D->2->1
E->2->1
ABDCE

为什么dfs的顺序是ABDCE？

A出发，直接进入2C
--C直接进入4E
----E的第一个邻居是2C，访问过了
----E的第二个邻居是1B，没访问过，进入1B
------B的第一个邻居是4E，访问过
------B的第二个邻居是3D，没访问过，进入3D
--------D的第一个……
……
后面是回溯了，略。

这样看，dfs的顺序不应该是ACEBD嘛？

其实是因为，并没有人说dfs一定要先进入当前点的哪个邻居呀。比如A，可以直接进入4E，也可以直接进入1B，这都是符合dfs的。

所以最大的问题还是：明明这是道多解题，却不开SPJ！！！

标程使用的非递归dfs，会一口气将当前点的所有邻居按照顺序扔进栈当中；而栈是先进后出的，所以当前点的所有邻居的实际访问的顺序就是倒过来的了。

 ##请在这里填写答案
    def dfs(self, V):
    # 从第 v 个顶点出发⾮递归实现深度优先遍历图 G
        visited = [] # 访问标志数组，其初值为"false"
        for i in range(0, 100):
            visited.append('false') # 访问标志数组初始化
        s = SqStack() # 构造⼀个空栈
        v = self.locate_vex(V)
        s.push(v) # 顶点 v 进栈
        while not s.stack_empty():
            k = s.pop() # 栈顶元素 k 出栈
            if visited[k] == 'false': # k 未被访问
                print(self.vertices[k].data, end='') # 访问第 k 个顶点
                visited[k] = 'true'
                p = self.vertices[k].firstarc # p 指向 k 的边链表的第⼀个边结点
                while p is not None: # 边结点⾮空
                    w = p.adjvex # 表示 w 是 k 的邻接点
                    if visited[w] == 'false':
                        s.push(w) # 如果 w 未访问，w 进栈
                    p = p.nextarc # p 指向下⼀个边结点

而我打算用递归dfs的方式改写的非递归dfs，为了通过这道题，就需要先把邻居列表反转一下了。

# 注意缩进
    def dfs(self, V):
        s = SqStack()
        book = []
        V=self.locate_vex(V)
        book.append(V)
        s.push(V)
        while not s.stack_empty():
            v = s.pop()
            print(self.vertices[v].data,end='')
            p=self.vertices[v].firstarc
            # 反转出边列表
            out=[]
            while p is not None:
                out.append(p.adjvex)
                p=p.nextarc

            for y in reversed(out):
                if y not in book:
                    s.push(y)
                    book.append(y)
                    break

有时候我在想，我往我的blog里面塞这种低质量题目的垃圾题解，有什么意义呢？这何尝不是一种制造垃圾……

6-4 距给定顶点距离最远的点-邻接矩阵

Floyd模板题。

# 注意缩进
    def shortest_path_max(self, V):
        dis=[INF for i in range(self.vexnum)]
        dis[self.locate_vex(V)]=0
        for i in range(0, self.vexnum):
            for j in range(0, self.vexnum):
                for k in range(0, self.vexnum):
                    if dis[j] + self.arcs[j][k] < dis[k]:
                        dis[k] = dis[j] + self.arcs[j][k]
        id=0
        for i in range(1, self.vexnum):
            if dis[id] < dis[i]:
                id = i
        return id

6-5 路径测试-邻接表

标记数组+dfs模板。

# 注意缩进
    def path_dfs(self, i, j):
        visited[i] = True
        if i == j:
            return True
        p = self.vertices[i].firstarc
        while p is not None:
            if not visited[p.adjvex]:
                if self.path_dfs(p.adjvex, j):
                    return True
            p=p.nextarc
        visited[i] = False
        return False

6-6 路径测试2-邻接表

dfs模板题。

##注意缩进
    def path_lenk(self, i, j, k):
        
        if i==j and k==0:
            return True
        if k<=0:
            return False
        visited[i] = True
        p = self.vertices[i].firstarc
        while p is not None:
            if not visited[p.adjvex]:
                if self.path_lenk(p.adjvex, j, k - 1):
                    return True
            p = p.nextarc
        visited[i] = False
        return False