CF contest 1909 Pinely Round 3 (Div. 1 + Div. 2) 题解（Vanilla的掉分赛）
Vanilla的掉分赛
$$
\color{purple}\large\textbf{世界上只有一种真正的英雄主义，}
$$
$$
\color{red}\large\textbf{就是认清了生活的真相后还依然热爱它。}
$$
$$
\color{gray}\large\texttt{ ——罗曼·罗兰}
$$
CF contest 1909 Pinely Round 3 (Div. 1 + Div. 2) Vanilla的掉分赛
绪言
Pinely Round 3 (Div. 1 + Div. 2) - Codeforces
A Distinct Buttons
Problem
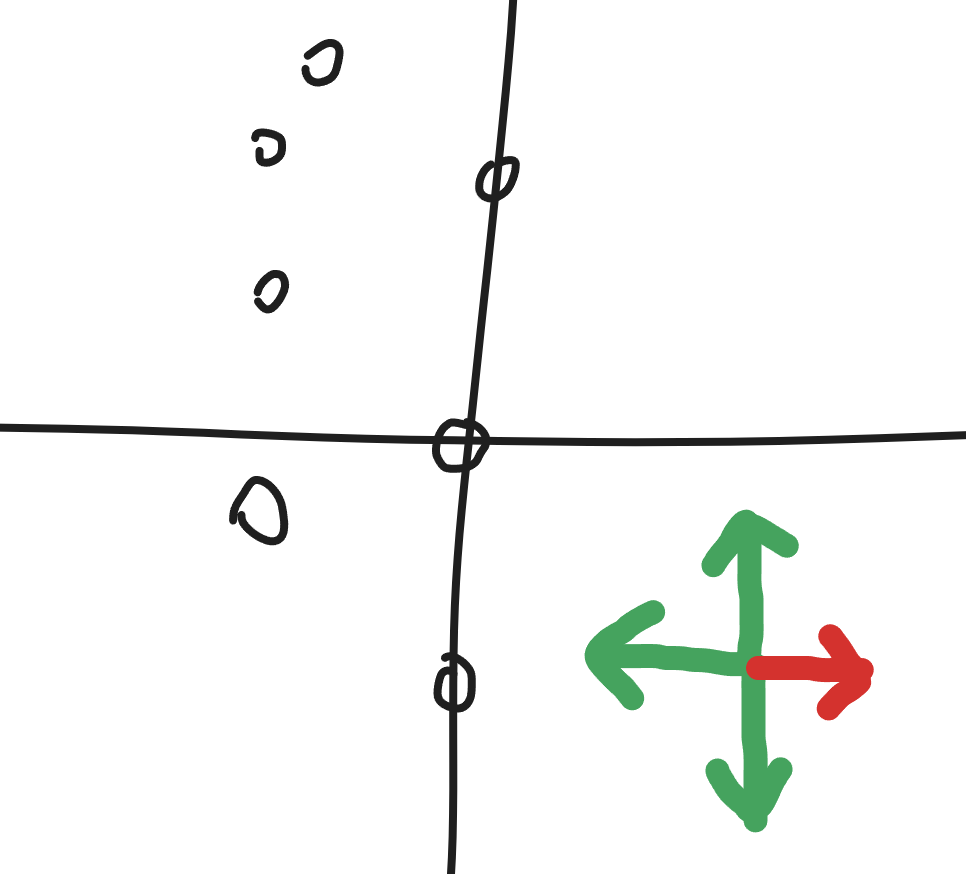
本来可以朝着上下左右移动，以依次（随便什么顺序）到达所有给定的坐标点。但是现在方向遥控器坏了，只能朝着三个方向移动了，请问现在是否还能到达所有给定的坐标点
Solution
只能朝着三个方向移动，也就是不能朝着某一个方向移动，并且这个方向是我们自选的。
假如不能往上走，那么还有整个第三第四象限可以走的（当然还包括x轴、y轴负半轴和坐标原点）；同理，如果所有点都出现在某个坐标轴的一侧的话，那么砍去一个方向依然还是能够全部走到的。
Code
int t;
int n;
int point[2000][2];
int main()
{
cin>>t;
while(t--)
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>point[i][0]>>point[i][1];
}
bool flag=1;
for(int i=0;i<n;i++)
{
if(point[i][0]<0) flag=0;
}
if(flag)
{
cout<<"YES"<<endl;
continue;
}
flag=1;
for(int i=0;i<n;i++)
{
if(point[i][1]<0) flag=0;
}
if(flag)
{
cout<<"YES"<<endl;
continue;
}
flag=1;
for(int i=0;i<n;i++)
{
if(point[i][0]>0) flag=0;
}
if(flag)
{
cout<<"YES"<<endl;
continue;
}
flag=1;
for(int i=0;i<n;i++)
{
if(point[i][1]>0) flag=0;
}
if(flag)
{
cout<<"YES"<<endl;
continue;
}
cout<<"NO"<<endl;
}
return 0;
}
Attention
注意考虑坐标轴和原点，所以直接用大于小于号判断是否在禁区中即可。
B Make Almost Equal With Mod
Problem
给一个长度为n的数列a，任意找到一个k使得将a全部模上k之后的数列中只有两种数（正好两种）
- 500组数据
- \(n \leq 100,1 \leq a_i \leq {10}^{17},k \leq {10}^{18}\)
Solution
偏向于构造题一点？
可以试试当\(k=2\)的时候，显然a中只会有0或者1两种数字。但是也可能会出现只有一种数的情况，比如当a全为偶数时，取模之后就全是0了。
这里以\(k=2\)时\(a_i\%k=0\)为例，\(a_i\%4\)只会有两种可能性：0或者2，所以我们考虑把k放宽到4.
但是这样依然有可能只有一种数（比如恰好\(a_i\%4=0\)的情况）怎么办？那就继续扩大k，直到余数出现了两种为止。
时间复杂度\({O}(tn\mathrm{log}k)\).
Code
#define N 10010
int n,t;
LL a[N];
set<LL>s;
void work()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
s.clear();
for(LL k=2;k<=1000000000000000000ll;k*=2)
{
s.clear();
for(int i=1;i<=n;i++) s.insert(a[i]%k);
if(s.size()==2)
{
cout<<k<<endl;
return;
}
}
}
Attention
注意数据范围需要开LL
注意数据范围k的上限要开\(10^{18}\)
这里用了set来维护有点小暴力了，这里set最多存两个数，直接用数组就好了
#define N 10010
int n,t;
LL a[N];
vector<LL>s;
void work()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
s.clear();
for(LL k=2;k<=1000000000000000000ll;k*=2)
{
s.clear();
for(int i=1;i<=n;i++)
{
bool flag=1;
for(unsigned int j=0;j<s.size();j++)
if(s[j]==a[i]%k)
{
flag=0;
break;
}
if(flag)
{
s.push_back(a[i]%k);
if(s.size()>2) continue;
}
}
if(s.size()==2)
{
cout<<k<<endl;
return;
}
}
}
C Heavy Intervals
Problem
给定n个区间左端点\(l_i\)和区间右端点\(r_i\)，你可以自由组合左右端点形成区间，但是要保证每个区间都是合法的（\(l_i<r_i\)）
再给n个权重\(c_i\)，可以与n个区间自由组合，这个区间的价值就是\(c_i \times (r_i-l_i)\)
总价值为
请重新组合\(l_i,r_i,c_i\)以最小化总价值
- 10000组数据
- \(n \leq 10^5,1 \leq l_i,r_i \leq 2\cdot{10}^{5},1\leq c \leq {10}^{7}\)
Solution
首先看乘法部分。由逆序<乱序<顺序可以知道我们要让最小的c乘以最长的区间，最大的c乘以最短的区间。
接下来分配左右端点。对于两对左右端点，有两种情况：
l=1 4
r= 3 6
这种情况由于要保证区间合法（\(l_i<r_i\)），只能1-3+4-6组合
l=1 3
r= 4 6
这种情况既可以1-4+3-6组合，也可以1-6+3-4组合
注意到两端区间长度之和相等，都是\(4-1+6-3=6-1+4-3=6\)，但是分配给两个区间的不一样了。第一种相交式的组合让两个长度更加平均，而第二种包含式的组合让两个区间长度差别更大。
当两段区间长度\(len_1,len_2(len_1<len_2)\)在乘以不同的权重\(c_1,c_2(c_1<c_2)\)时，可以发现：
即让两端区间的长度差别更大，并且与权重c形成逆序，可以得到更小的总价值
于是得出一个选择策略：
从最后一个左端点开始，寻找在其右侧的最靠左的右端点，与之匹配成区间
通过从后往前为左端点匹配，保证在不会抢占其右侧的左端点匹配右端点，同时使得最近的右端点与之匹配
这里使用map记录所有右端点的坐标，使用upper_bound为每个左端点查找最合适的右端点，并且匹配后将被匹配的右端点从map中移除
最后乘以倒序的c再求和，即为最小总价值。
时间复杂度\(O(tn\log n)\).
Code
#define N 1000010
int t;
int n;
LL l[N],r[N],c[N];
bool cmp(LL a,LL b)
{
return a>b;
}
map<int,int>m;
int main()
{
cin>>t;
while(t--)
{
cin>>n;
for(int i=0;i<n;i++) cin>>l[i];
for(int i=0;i<n;i++) cin>>r[i],m[r[i]]++;
for(int i=0;i<n;i++) cin>>c[i];
sort(l,l+n);
sort(c,c+n,cmp);
for(int i=n-1;i>=0;i--)
{
if(m.upper_bound(l[i])!=m.end())
{
int rr=(*m.upper_bound(l[i])).first;
m[rr]--;
if(m[rr]==0) m.erase(rr);
r[i]=rr-l[i];//这里借用r来存r[i]-l[i]
}
}
sort(r,r+n);
LL ans=0;
for(int i=0;i<n;i++)
{
ans+=c[i]*(r[i]);
}
cout<<ans<<endl;
}
return 0;
}
Tips
噢，刚刚写数据范围的时候发现l和r都比较小（\(2\cdot10^5\)）也就是说可以直接开值域数组记录r，可以把map换成别的算法了
求区间最小位置且动态修改——线段树？怎么反而变复杂了呢……我越想越麻烦啊……
看了一眼Tutorial，这不就是括号匹配嘛，直接上堆栈啊！
复习一下：首先将\(l_n\)右侧的\(r_i\)依次放入栈中，栈顶就是最接近\(l_n\)的\(r_i\)了
取出栈顶与\(l_n\)匹配，并出栈
现在为\(l_{n-1}\)匹配：先将\(l_{n-1}\)右侧的\(r_i\)继续入栈，然后取出栈顶与之匹配出栈
继续匹配到\(l_1\)
D Split Plus K
Problem
给定k，将一个长度为n的数列a进行以下操作，用最小的步数使其元素全部相同，若不能则输出-1
- 在a中选择一个元素x
- 构造一对数\((y,z)\)，满足\(y+z=x+k\)
- 用\(y,z\)代替数列a中原本的x
Solution
参考了Tutorial
首先将等式\(x+k=y+z\)变形为\((x-k)=(y-k)+(z-k)\)
这意味着，本来对一个数\(x\)进行操作时，会使得数列a的和发生变化；而如果我们事先将数列a中所有的元素\(x\)都换成\(x'=x-k\)，那么对于\(x'\)操作时，就只需直接将\(x'\)分裂成两个数\(y',z'\)即可.
现在问题简化为：
对于数列\(a'\)，每次选择一个数裂成两个数，用最小的步数使其元素全部相同。
假如将\(a'\)最终分成了p个元素，每个元素都是m，那么也就是说最后一步完成之后，数列\(a'\)会变成p个m
这时候从最后一步往前反推一步，也就是两个m合并为一个2m……继续合并，会发现无论怎么合并，合并出来的数字都是m的倍数，且正负性永远与m相同
这意味着
- m是所有\(a'_i\)的因子
- 所有\(a'_i\)同号
所以结论
-
为了使得步数最少，答案即为最小公倍数\(|m|=\mathrm{gcd}(|a'_i|)\)
-
若\(a'_i\)不同号或者不皆为0，则无解
-
若\(a'_i\)皆为0，则m=0，
最小操作次数\(T=p-n=\frac{\sum a'_i}{m}-n\)
时间复杂度\(O(n+\mathrm{log}(\max a_i))\).
Code
#define N 200010
int t;
int n;
LL k;
LL a[N],ans,sum;
bool zheng,fu,zero;
LL gcd(LL x,LL y)
{
if(y==0) return x;
return gcd(y,x%y);
}
int main()
{
t=read();
while(t--)
{
n=read();k=read();zheng=fu=zero=1;sum=0;
//cout<<"gcd="<<gcd(n,k)<<endl;
for(int i=0;i<n;i++) a[i]=read()-k,sum+=a[i];
for(int i=0;i<n;i++)
{
if(a[i]>0) fu=zero=0;
if(a[i]==0) fu=zheng=0;
if(a[i]<0) zheng=zero=0;
}
if(zero)
{
cout<<"0"<<endl;
}
else if(zheng)
{
ans=a[0];
for(int i=1;i<n;i++) ans=gcd(ans,a[i]);
cout<<sum/ans-n<<endl;
}
else if(fu)
{
ans=-a[0];sum=-sum;
for(int i=1;i<n;i++) ans=gcd(ans,-a[i]);
cout<<sum/ans-n<<endl;
}
else cout<<"-1"<<endl;
}
return 0;
}
