记一道有趣的交互题 noi.ac #2035歪比巴卜

记一道有趣的交互题 noi.ac #2035歪比巴卜

Problem

Alice手上有两个\(\le n\)且不同的正整数\(x,y\)，Bob手上有一个正整数\(z\)，已经确认是\(x\)或\(y\)中的某一个。 现在除了Alice可以告诉Bob一个正整数\(k\)外，两人不能有任何交流，而Bob需要根据这个数确定\(z=x\)还是\(z=y\)。 请你实现一个程序，帮助Alice决定正整数\(k\)，以及帮助Bob根据\(k\)确定\(z=x\)还是\(z=y\)。

你需要实现下面的三个函数：

void init()

对你的程序进行初始化。该函数只会在程序开始运行时被调用恰好一次。

int helpAlice(int x,int y)}

给定一组互不相同的\(x,y\)，你要帮助Alice确定kk，并将其作为返回值返回。不是正整数的返回值会导致你获得0分。

int helpBob(int z,int k)

给定一组\(z,k\)，保证z是之前某次调用helpAlice(x,y)中的\(x\)或\(y\)，且\(k\)是那次调用函数的返回值。 你要帮助Bob确定\(z=x\)还是\(z=y\)并返回相应的值，若\(z=x\),返回1，否则一定有\(z=y\),返回0。不正确的返回值会导致你获得0分。

评测时，交互程序将会首先调用一次init()，然后调用不超过T次helpAlice()和helpBob()，如果任何一次调用的返回值不合法或不正确， 则直接结束并返回00分。如果全部正确，则按照如下如下标准评分：

令所有helpAlice()的返回值中的最大值为R，则你的得分为：

评测时，保证交互程序使用的时间不超过0.5s,空间不超过128MB。

Example

样例

假设交互程序依次调用了如下函数，则一种合法的返回值如下所示：

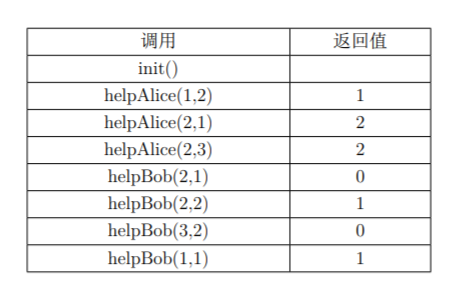
数据范围与约定

对于\(100\%\)的数据，\(n=920\)，\(T=3\times10^6\)。

Solution

首先讲讲交互格式。

最好的方法就是列出1分的代码，应该就可以立马懂了。

void init()
{
	
}
int helpAlice(int x,int y)
{
	return x;
}
int helpBob(int z,int k)
{
	if(k==z) return 1;
	return 0;
}

\(x,y\le920\)，而要得满分则需要做到\(R\le12\)。

这\(920\)和\(12\)之间有什么联系呢？恐怕只有出题人才能想得到吧……

发现\(\binom{12}{6}=924>920\)，所以可以将从1_{12中选6个的方案来唯一表示1}920中的每一个数。

准确地，对于每次调用函数helpAlice()，记表示\(x\)的集合为\(X\)，表示\(y\)的集合为\(Y\)，我们找到任意一个在\(X\)当中且不在\(Y\)当中的元素并将其返回。（由于\(x\neq y\)，这样的元素必定存在，）

对于每次调用函数helpBob()，记表示\(z\)的集合为\(Z\)，若\(k\in Z\)，则说明\(z=x\)；否则说明\(z=y\).

这样，我们就在tyq把香农的棺材板撬开之前做完了这道题，时间复杂度\(O(2^{12}+T)\).

Code

/**************************************************************
 * Problem:
 * Author: Vanilla_chan
 * Date: 20210318
**************************************************************/
int a[924],h[4096],cnt;
void dfs(int x,int y,int z)
{
	if(x==12&&y==6)
	{
		a[cnt++]=z;
		return;
	}
	if(x<12&&y<=6) dfs(x+1,y,z),dfs(x+1,y+1,z+(1<<x));
}
void init()
{
	dfs(0,0,0);
	for(int i=1;i<4096;i++)
	{
		if(i&1) h[i]=0;
		else h[i]=h[i>>1]+1;
	}
}
int helpAlice(int x,int y)
{
	x--;
	y--;
	return h[a[x]&(~a[y])]+1;
}
int helpBob(int z,int k)
{
	z--;
	k--;
	if(a[z]>>k&1) return 1;
	return 0;
}