洛谷 P3268 [JLOI2016]圆的异或并

洛谷 P3268 [JLOI2016]圆的异或并

题目描述

在平面上有两两不相交的\(n\)个圆，即其关系只有相离和包含。求这些圆的异或面积并。

异或面积并为：当一片区域被奇数个圆包含则计算其面积，否则不计算。

输出所有圆的异或面积并除以\(\pi\)的结果。

\(n\le 200000\)。

Solution

前置知识：扫描线，set。

可以发现，由于圆是不相交的，那么这种包含关系可以看作是一棵森林（许多有根树构成的图）。

比如像这个几个圆

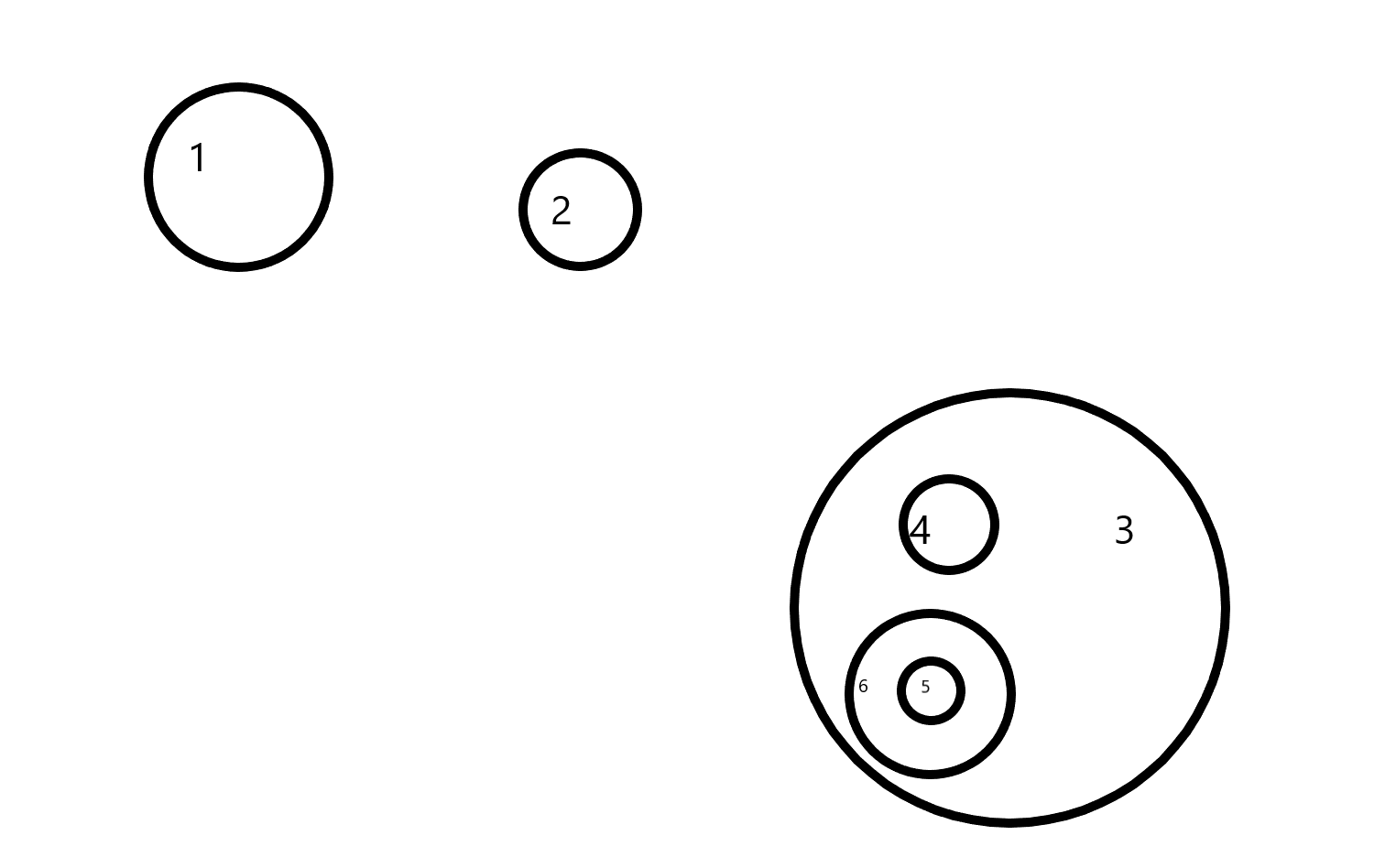
可以变成

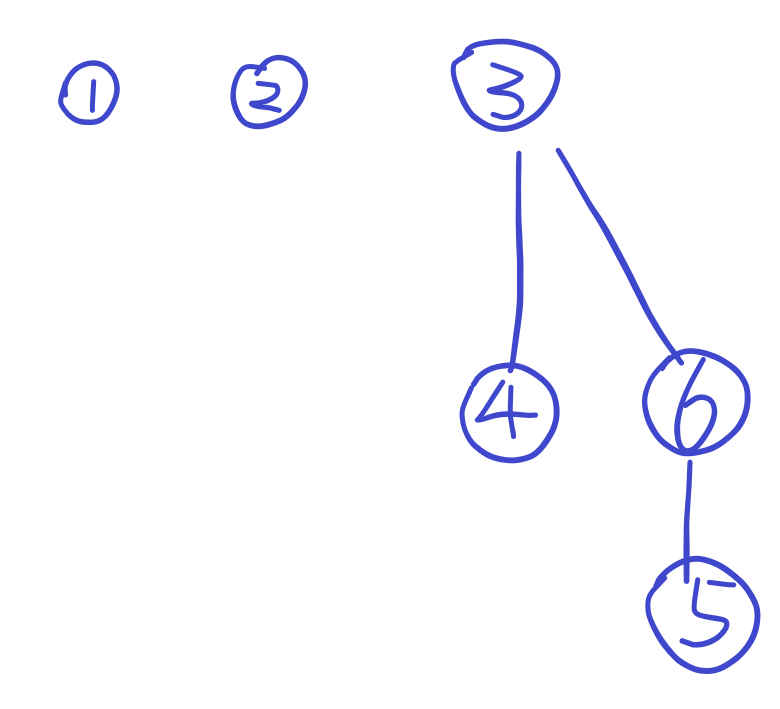
设每个根的深度为1，那么深度为奇数的节点的面积是需要加上的，深度为偶数的节点的面积是需要减去的。

即

\[ans=\sum_{i=1}^nr_i^2\times(-1)^{dep_i+1} \]

同扫描线的思想，我们模拟出有一条垂直于\(x\)轴的直线从左向右移动。

• 当其与某个圆开始触碰到的时候，就将这个圆拆分为上半圆和下半圆插入set中。这个set是按照圆的高度排序的。由于保证了圆和圆之间不相交，所以可以直接计算扫描线与半圆的交点作为关键字排序。圆和圆之间不相交保证了这个关键字的相对大小一定不会变。

查询刚刚插入的圆的上半圆的前驱（在set中的所有半圆中，在当前圆下方最近的半圆）。如果它的前驱是一个上半圆，那么当前圆的深度等于其前驱的深度；若前驱是一个下半圆，那么说明当前圆被其前驱所包含，深度为前驱的深度+1。

• 遇到圆的右边界就直接将其两个半圆从set中删除即可。

因为set中要插入同一id的两个半圆，那么只要用up表示当前圆是上半圆还是下半圆即可。重载运算符时，可以比较当前扫描线与半圆的交点，也可以以圆心的纵坐标为第一关键字，以上/下半圆为第二关键字进行比较。

注意，如果是以扫描线与半圆的交点进行比较的话，在扫描线进入/离开一个圆的时候，扫描线与两个半圆的交点会重合。需要在比较函数中将上半圆的交点纵坐标加上一个\(eps\)即可。

Code

我的排序方法是比较当前半圆和扫描线的交点。

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<limits.h>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#ifdef TH
#define debug printf("Now is %d\n",__LINE__);
#else
#define debug
#endif
using namespace std;

template<class T>inline void read(T&x)
{
	char ch=getchar();
	int fu;
	while(!isdigit(ch)&&ch!='-') ch=getchar();
	if(ch=='-') fu=-1,ch=getchar();
	x=ch-'0';ch=getchar();
	while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
	x*=fu;
}
inline LL read()
{
	LL x=0,fu=1;
	char ch=getchar();
	while(!isdigit(ch)&&ch!='-') ch=getchar();
	if(ch=='-') fu=-1,ch=getchar();
	x=ch-'0';ch=getchar();
	while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
	return x*fu;
}
int G[55];
template<class T>inline void write(T x)
{
	int g=0;
	if(x<0) x=-x,putchar('-');
	do{G[++g]=x%10;x/=10;}while(x);
	for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar('\n');
}
#define N 200010
int n,nowx;
LL X[N],Y[N],R[N];
struct Opt
{
	LL pos;
	int x;
	bool insert;
	Opt(LL a=0,int b=0,bool c=0)
	{
		pos=a,x=b,insert=c;
	}
	IL bool operator<(const Opt& z)const
	{
		return pos<z.pos;
	}
};
vector<Opt>opt;
bool dep[N];
#define eps 1e-6
struct O
{
	int x;
	bool up;
	O(int xx=0,bool u=1)
	{
		x=xx,up=u;
	}
	double calc()const
	{
		if(up) return Y[x]+sqrt(R[x]*R[x]-(X[x]-nowx)*(X[x]-nowx))+eps;
		return Y[x]-sqrt(R[x]*R[x]-(X[x]-nowx)*(X[x]-nowx));
	}
	IL bool operator<(const O& z)const
	{
		return calc()<z.calc();
	}
};
set<O>s;
set<O>::iterator it;
int main()
{
	n=read();
	for(int i=1;i<=n;i++)
	{
		X[i]=read();
		Y[i]=read();
		R[i]=read();
		opt.push_back(Opt(X[i]-R[i],i,1));
		opt.push_back(Opt(X[i]+R[i],i,0));
	}
	sort(opt.begin(),opt.end());
	LL ans=0;
	for(int i=0;i<opt.size();i++)
	{
		nowx=opt[i].pos;
		if(opt[i].insert)
		{
			it=s.insert(O(opt[i].x,1)).first;
			if(it==s.begin())
			{
				dep[opt[i].x]=1;
			}
			else
			{
				it--;
				if(it->up)
				{
					dep[opt[i].x]=dep[it->x];
				}
				else
				{
					dep[opt[i].x]=dep[it->x]^1;
				}
			}
			s.insert(O(opt[i].x,0));
			if(dep[opt[i].x]) ans+=R[opt[i].x]*R[opt[i].x];
			else ans-=R[opt[i].x]*R[opt[i].x];
		}
		else
		{
			s.erase(O(opt[i].x,1));
			s.erase(O(opt[i].x,0));
		}
	}
	write(ans);
	return 0;
}

总结

扫描线是一种重要的思想。在其应用的过程中常常需要用到set​，线段树等数据结构进行维护。