【2020.11.30提高组模拟】删边(delete) 题解

题意简述

给一棵树删边，每次删的代价为这条边所连的两个点的子树中最大点权值。

求删光的最小代价。

\(n\le100000\).

Solution

正着思考发现没有什么好的思路，贪心的话会后效性。不妨反过来考虑。

这时题目变成了：给\(n\)个点，每次连通两个点集，代价为两个点集中最大点权之和。

例如这个图

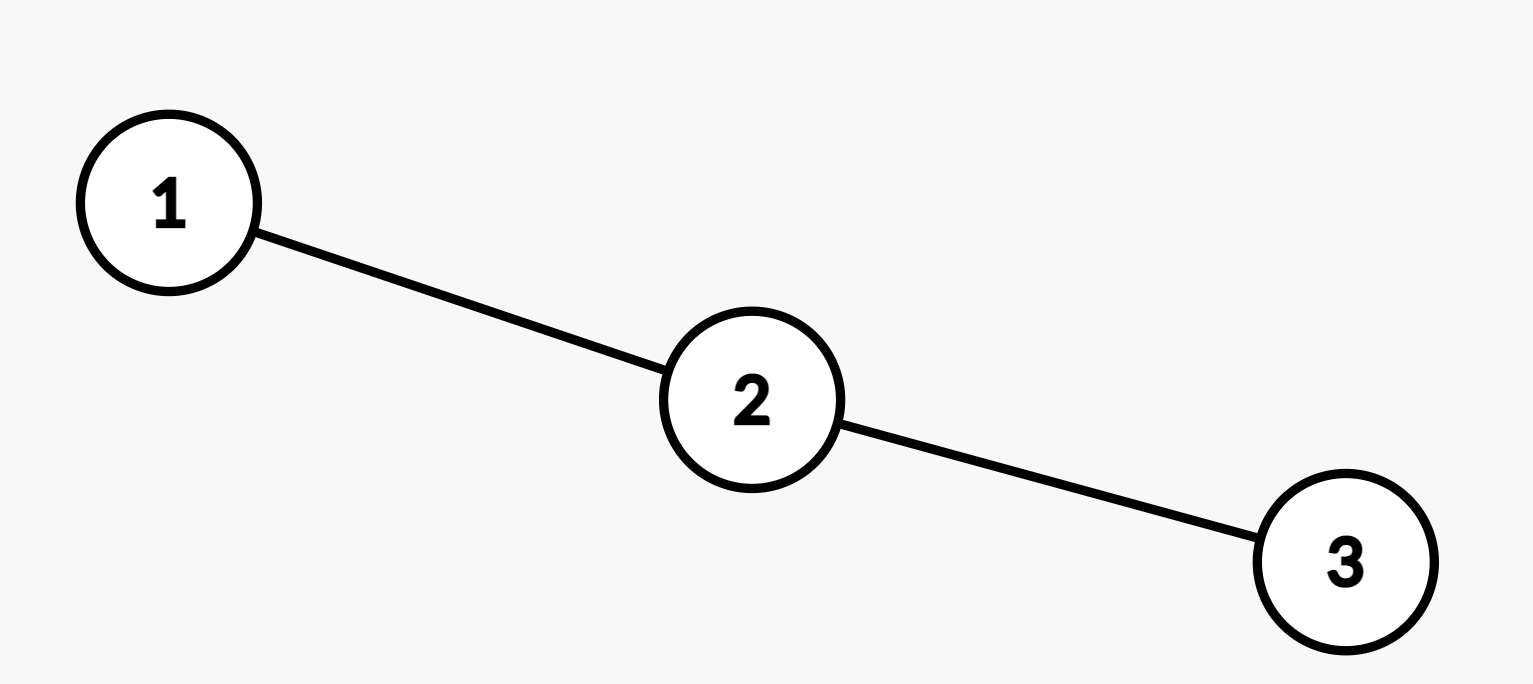
首先，每个点都是独立的。

那么你会先加入\(1-2\)还是\(2-3\)呢？

如果先加入\(2-3\)，代价为\(2+3\)，接下来再加入点\(1\)时，\(2-3\)所产生的贡献是\(3\)。

如果而后还有一些集合需要并进来时，当前集合所产生的贡献为\(3\)，很大很浪费。

所以，我们要让点权大的点以后再合并，点权小的点先合并。

所以初始化时先把边权设为其所连两点的点权中更大的那一个。对所有边按照边权排序，再用类似并查集的方法合并同时维护集合中的最大点权。

以上。

Code

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#ifdef TH
#define debug printf("Now is %d\n",__LINE__);
#else
#define debug
#endif
using namespace std;

template<class T>inline void read(T&x)
{
	char ch=getchar();
	int fu;
	while(!isdigit(ch)&&ch!='-') ch=getchar();
	if(ch=='-') fu=-1,ch=getchar();
	x=ch-'0';ch=getchar();
	while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
	x*=fu;
}
inline int read()
{
	int x=0,fu=1;
	char ch=getchar();
	while(!isdigit(ch)&&ch!='-') ch=getchar();
	if(ch=='-') fu=-1,ch=getchar();
	x=ch-'0';ch=getchar();
	while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
	return x*fu;
}
int G[55];
template<class T>inline void write(T x)
{
	int g=0;
	if(x<0) x=-x,putchar('-');
	do{G[++g]=x%10;x/=10;}while(x);
	for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar('\n');
}
int n,f[100010],mx[100010],a[100010];
LL ans;
int getf(int x)
{
	if(f[x]==x) return x;
	return f[x]=getf(f[x]);
}
void merge(int x,int y)
{
	x=getf(x);
	y=getf(y);
	if(x!=y)
	{
		ans+=mx[x]+mx[y];
		mx[x]=max(mx[x],mx[y]);
		f[y]=x;
	}
}
struct edge
{
	int x,y;
	edge(int xx=0,int yy=0){x=xx,y=yy;}
//	int v()const{return max(a[x],a[y]);}
	bool operator<(const edge & z)const
	{
		return max(a[x],a[y])<max(a[z.x],a[z.y]);
	}
};
vector<edge>e;
int main()
{
//	freopen("delete.in","r",stdin);
//	freopen("delete.out","w",stdout);
	n=read();
	for(int i=1;i<=n;i++) f[i]=i,mx[i]=a[i]=read();
	for(int i=1;i<n;i++) e.push_back(edge(read(),read()));
	sort(e.begin(),e.end());
	for(unsigned i=0;i<e.size();i++)
	{
		merge(e[i].x,e[i].y);
	}
	cout<<ans;
	return 0;
}