【2020.11.19提高组模拟】倍数区间interval 题解
【2020.11.19提高组模拟】倍数区间interval 题解
题目描述
定义在序列\(a_1,a_2,\dots,a_n\)上的合法区间\([L,R]\)为满足\(\exists k\in [L,R],\forall i\in [L,R],a_k\mid a_i\)。
即存在一个数\(a_k\),满足区间内所有的数都是\(a_k\)的倍数。
求最长的合法区间长度并输出这些区间的左端点。
Solution
又是区间问题。
首先找到几个结论:
1.\(a_k\)一定是这个区间内最小的数。
2.\(a_k\mid 区间gcd\)。
第一个很显然,倍数当然要大于或等于自己的。
第二个也很显然,\(区间gcd\)就是这个区间内所有数的因数的交集。
那么我们可以用ST表预处理出区间\(gcd\),然后对于每个数当作它是那个\(a_k\),左右各自二分出最远的合法区间即可。
复杂度\(O(n\log^2 n)\)。
Code-ST
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#define debug printf("Now is %d\n",__LINE__);
using namespace std;
template<class T>inline void read(T&x)
{
char ch=getchar();
int fu;
while(!isdigit(ch)&&ch!='-') ch=getchar();
if(ch=='-') fu=-1,ch=getchar();
x=ch-'0';ch=getchar();
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
x*=fu;
}
inline int read()
{
int x=0,fu=1;
char ch=getchar();
while(!isdigit(ch)&&ch!='-') ch=getchar();
if(ch=='-') fu=-1,ch=getchar();
x=ch-'0';ch=getchar();
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*fu;
}
int G[55];
template<class T>inline void write(T x)
{
int g=0;
if(x<0) x=-x,putchar('-');
do{G[++g]=x%10;x/=10;}while(x);
for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar(' ');
}
int n;
int lg[1000010];
int gcd[1000010][24];
int GCD(int a,int b)
{
// cout<<"gcd a="<<a<<" b="<<b<<" ";
int t;
while(b)
{
t=b;
b=a%b;
a=t;
}
// cout<<"gcd="<<a<<endl;
return a;
}
void pre()
{
lg[1]=0;
for(re int i=2;i<1000010;i++) lg[i]=lg[i>>1]+1;
for(re int j=1;j<=22;j++)
{
for(int i=1;i+(1<<j)-1<=n;i++)
{
gcd[i][j]=GCD(gcd[i][j-1],gcd[i+(1<<(j-1))][j-1]);
}
}
}
int ask(int l,int r)
{
return GCD(gcd[l][lg[r-l+1]],gcd[r-(1<<lg[r-l+1])+1][lg[r-l+1]]);
}
int maxans;
int ans[500010];
int sze;
//out:sze-maxans\nans
int main()
{
freopen("interval.in","r",stdin);
freopen("interval.out","w",stdout);
n=read();
for(int i=1;i<=n;i++) gcd[i][0]=read();
pre();
for(int k=1,L,R,l,r,mid;k<=n;k++)
{
l=1,r=k;
while(l!=r)
{
mid=(l+r)/2;
if(ask(mid,k)%gcd[k][0]==0) r=mid;
else l=mid+1;
}
L=l;
l=k,r=n;
while(l<r)
{
mid=(l+r+1)/2;
if(ask(k,mid)%gcd[k][0]==0) l=mid;
else r=mid-1;
}
R=r;
// cout<<L<<" "<<R<<endl;
if(R-L>maxans) maxans=R-L,sze=0;
if(R-L==maxans&&ans[sze]!=L) ans[++sze]=L;
}
printf("%d %d\n",sze,maxans);
for(int i=1;i<=sze;i++) write(ans[i]);
return 0;
}
upd
但是其实有一种\(O(n\log n)\)的做法!
我在考试的时候打暴力时打的就是这样的优化,我觉得它的时间过不去,但是其实比上面的算法还要暴力,复杂度还要小!
利用第一个性质——自己的倍数的倍数也是自己的倍数。
那么每次对一个数扩展完之后记录一下区间的左右端点。
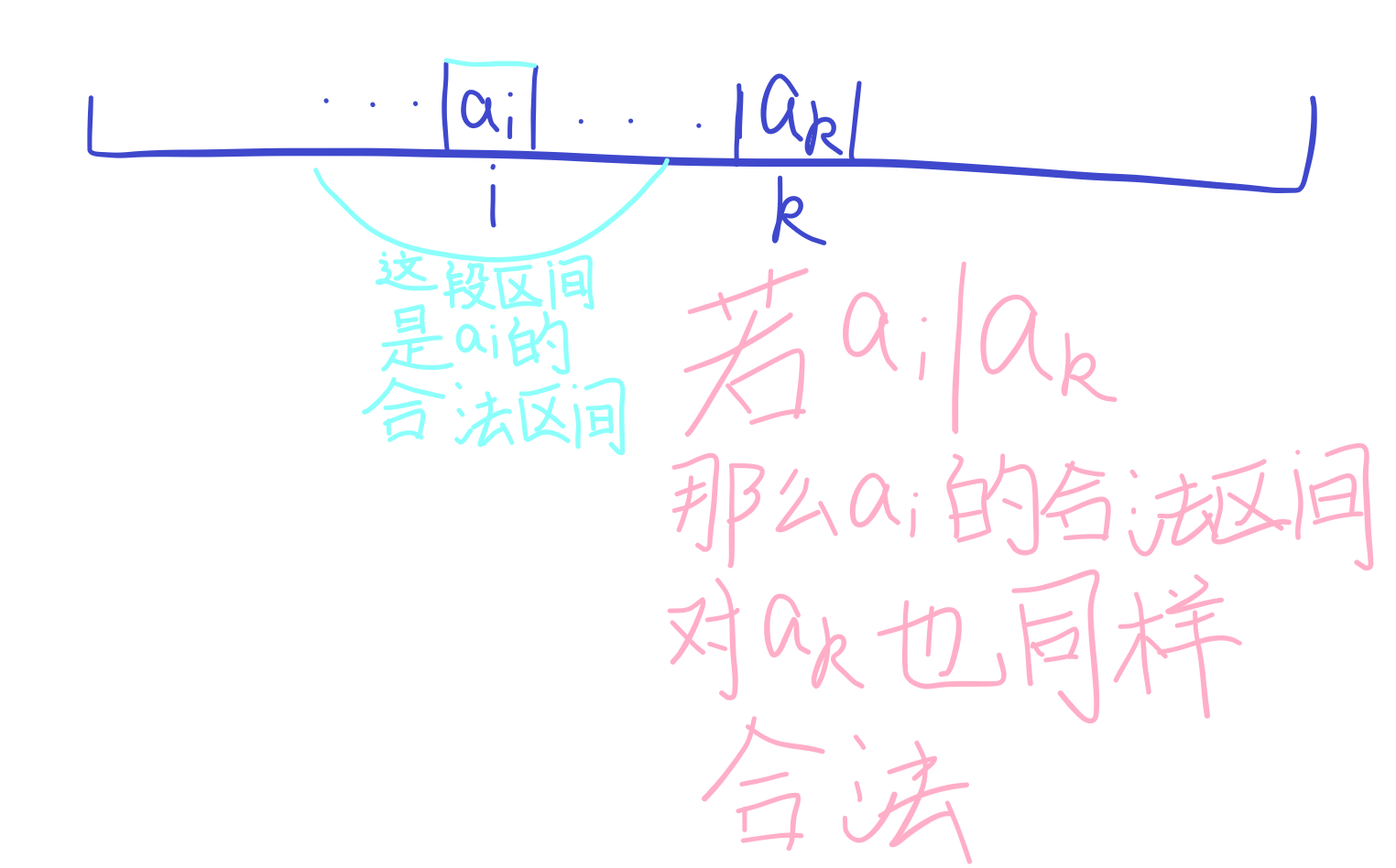
之后对后面的数\(a_k\)扩展时,若发现有一个\(a_k\mid a_i(i<k)\),那么当前的区间的左端点可以直接跳转到\(a_i\)的合法区间左端点。同理,右端点也可以跳。
Code
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#define debug printf("Now is %d\n",__LINE__);
using namespace std;
template<class T>inline void read(T&x)
{
char ch=getchar();
int fu;
while(!isdigit(ch)&&ch!='-') ch=getchar();
if(ch=='-') fu=-1,ch=getchar();
x=ch-'0';ch=getchar();
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
x*=fu;
}
inline int read()
{
int x=0,fu=1;
char ch=getchar();
while(!isdigit(ch)&&ch!='-') ch=getchar();
if(ch=='-') fu=-1,ch=getchar();
x=ch-'0';ch=getchar();
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*fu;
}
int G[55];
template<class T>inline void write(T x)
{
int g=0;
if(x<0) x=-x,putchar('-');
do{G[++g]=x%10;x/=10;}while(x);
for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar(' ');
}
int n;
int a[500010];
int kmp[500010],gkd[500010];
int ans;
int L[500010];
int sze;
//out:size-ans\nL
int main()
{
freopen("interval.in","r",stdin);
freopen("interval.out","w",stdout);
n=read();
for(re int i=1;i<=n;i++) a[i]=read(),kmp[i]=i;
for(re int i=1,l,r;i<=n;i++)
{
// debug cout<<"i="<<i<<endl;
for(l=i-1,r=i+1;l>0;l--)
{
// debug
if(a[l]<a[i]||a[l]%a[i]) break;
// debug
// cout<<"l="<<l<<endl;
l=kmp[l];
r=max(r,gkd[l]);
}
l++;
kmp[i]=l;
for(;r<=n;r++)
{
// debug
if(a[r]<a[i]||a[r]%a[i]) break;
// debug
}
r--;
gkd[i]=r;
if(r-l>ans)
{
ans=r-l;
sze=0;
}
if(r-l==ans&&L[sze]!=l)
{
L[++sze]=l;
}
}
printf("%d %d\n",sze,ans);
for(int i=1;i<=sze;i++)
{
write(L[i]);
}
return 0;
}
小结
注意最后的结果要判重哦!否则\(score-=30pts\)!

