树状数组小结

树状数组小结

背景

树状数组本质是区间前缀和，但是众所周知，暴力和前缀和各有优缺点……

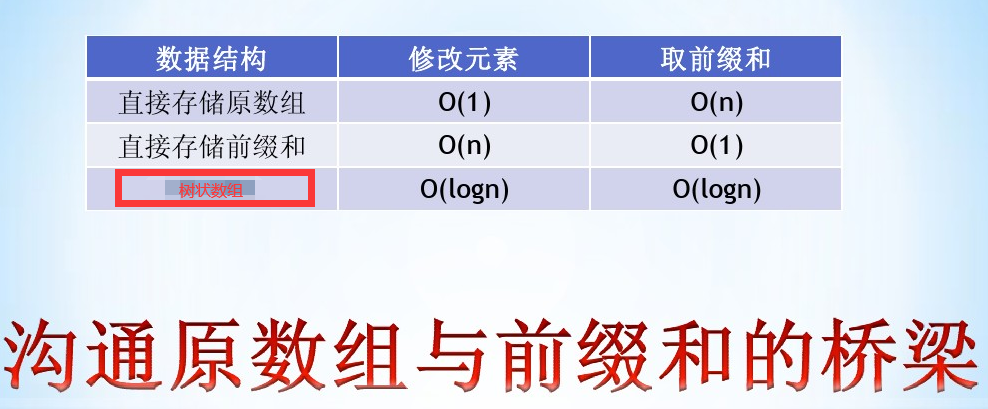
（图片中本来是线段树的，但是其实差不多吧）

所以诞生了树状数组这个东西。

功能

树状数组分为以下几步

声明部分

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <map>
#include <set>
#include <queue>
#include <vector>
#define IL inline
#define re register
#define LL long long
using namespace std;

IL LL read() {
    LL ans = 0;
    bool fu = 0;
    char ch = getchar();
    while ((ch > '9' || ch < '0') && ch != '-') ch = getchar();
    if (ch == '-')
        fu = 1, ch = getchar();
    while (ch <= '9' && ch >= '0') ans = (ans << 3) + (ans << 1) + (ch ^ 48), ch = getchar();
    if (fu)
        ans *= -1;
    return ans;
}
LL n, m;
LL a[1000010];
LL s[1000010];
LL b[1000010];

建树

IL void add(LL x, LL y) {
    for (; x <= n; x += x & (-x)) a[x] += y;
}
int main()
{
    n = read();
    m = read();
    for (re int i = 1; i <= n; i++){
        add(i,read());
}    

使用了add函数，见下面的单点修改。

当然这是简单的O(nlogn)建树，还有更快的：

更快的建树

    n = read();
    m = read();
    for (re int i = 1; i <= n; i++){
        b[i]=read();
        a[i]+=b[i];
        a[i+(i&-i)]+=a[i];
    }    

时间复杂度为O(n)

单点修改

IL void add(LL x, LL y) {
    for (; x <= n; x += x & (-x)) a[x] += y;
}

查询前缀和

IL LL ask(LL x) {
    re LL ans = 0;
    for (; x; x -= x & (-x)) ans += a[x];
    return ans;
}

由此可以查询区间。

Code

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <map>
#include <set>
#include <queue>
#include <vector>
#define IL inline
#define re register
#define LL long long
using namespace std;

IL LL read() {
    LL ans = 0;
    bool fu = 0;
    char ch = getchar();
    while ((ch > '9' || ch < '0') && ch != '-') ch = getchar();
    if (ch == '-')
        fu = 1, ch = getchar();
    while (ch <= '9' && ch >= '0') ans = (ans << 3) + (ans << 1) + (ch ^ 48), ch = getchar();
    if (fu)
        ans *= -1;
    return ans;
}
LL n, m;
LL a[1000010];
LL s[1000010];
LL b[1000010];
IL void add(LL x, LL y) {
    for (; x <= n; x += x & (-x)) a[x] += y;
}
IL LL ask(LL x) {
    re LL ans = 0;
    for (; x; x -= x & (-x)) ans += a[x];
    return ans;
}
int main() {
    n = read();
    m = read();
    for (re int i = 1; i <= n; i++){
        b[i]=read();
        a[i]+=b[i];
        a[i+(i&-i)]+=a[i];
    }    
    LL t, x, y;
    while (m--) {
        t = read();
        x = read();
        y = read();
        if (t == 1)
            add(x, y);
        else
            cout << ask(y) - ask(x - 1) << endl;
    }

    return 0;
}

小结

这应该是最快的RSQ算法了。如果这都过不去请参见zkw线段树……

（我还真就遇到过……）

#include<cstdio>
#define ll long long
#define go(i,j,n,k) for(ll i=j;i<=n;i+=k)
#define fo(i,j,n,k) for(ll i=j;i>=n;i-=k)
#define mn 1000010
inline ll read(){ll x=0,f=1;char ch=getchar();while(ch>'9'||ch<'0'){if(ch=='-')f=-f;ch=getchar();    }
                while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;}
ll z[mn << 2], M, n, m;
inline void update(ll rt){z[rt] = z[rt<<1] + z[rt<<1|1];}
inline void build(){for(M=1;M<n+2;M<<=1);go(i,M+1,M+n,1)z[i]=read();fo(i,M,1,1) update(i);}
inline void modify(ll now,ll v){for(z[now+=M]+=v,now>>=1;now;now>>=1)update(now);}
inline ll query(ll l,ll r){ll ans=0;for(--l+=M,++r+=M;l^r^1;l>>=1,r>>=1){if(~l&1)ans+=z[l^1];if(r&1)ans+=z[r^1];}return ans;}
int main(){
    n=read(),m=read();build();
    go(i,1,m,1){
        int s=read(),x=read(),y=read();
        if(s==1)modify(x,y);else printf("%lld\n",query(x,y));
    }
}

树状数组的拓展

 

事实上，树状数组存在许多拓展。

比如最值维护，只要只需要查询前缀最值，且求改只涉及取最值操作，也是可以做的。

而树状数组可以区间修改，这里不进行讨论。

树状数组可以和主席树搭配使用，超出noip范围，也不讨论。