启智树提高组day4T1 T1(t1.cpp,1s,512MB)
启智树提高组day4T1 T1(t1.cpp,1s,512MB)

题面描述
对⼀个⻓度为2n 的实数序列A考虑下列问题:
设S为序列中所有元素的和。你可以做下列操作n次:
- 选择两个未被选中过的下标i和j,要求i≠j ;
- 将 Ai变为不超过Ai的最⼤整数,即将 Ai向下取整;
- 将Aj变为不小于Aj的最小整数,即将Aj向上取整。
要求操作完成之后,新的序列中所有元素之和S'和S的差的绝对值尽量小。
现在给你⼀个⻓度为m的实数序列B,有Q组询问。每组询问要求将这个序列的⼀个区间作为上述问题中的A求解。
输入格式
第⼀⾏两个正整数m ,Q 。第⼆⾏ m个 0到 10^4之间的实数Ai ,每个实数都恰好保留了三位小数。
然后Q⾏,每⾏两个正整数Li,Ri ,表⽰此次需要求解的区间为[Li,Ri] ,保证。
输出格式
Q⾏,每⾏⼀个实数,保留三位小数,表⽰此次询问中 和 的差的绝对值可能取到的最小值。
样例输入

样例输出
样例解释
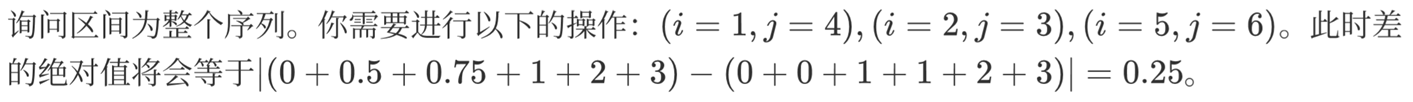
数据范围

解题思路
我的基本想法
输入这个数组,记录每个数字的小数部分;
取出并复制其需要区间
排序,但是要先去掉小数区间为0的,因为零的话既可以向上取整,也可以向下取整
一个循环,循环区间中不为0 的数字的个数的一半。每次循环时取出一个最小值和最大值;
但是如果这时,最小值>0.5的话就要考虑使用0来补位。最大值同理。
1 while(li<=ri) 2 3 { 4 5 if(range[li]>0.5&&zero) li--,zero--; 6 7 else{ 8 9 ans-=range[li]; 10 11 // cout<<"ans+="<<range[li]<<endl; 12 13 } 14 15 if(range[ri]<=0.5&&zero) ri++,zero--; 16 17 else{ 18 19 ans+=1-range[ri]; 20 21 // cout<<"ans+=1-"<<range[ri]<<endl; 22 23 } 24 25 li++; 26 27 ri--; 28 29 }
Code

1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 #include<cstring> 5 #include<cmath> 6 #include<iomanip> 7 #include<map> 8 #include<set> 9 #include<queue> 10 #include<vector> 11 #define IL inline 12 #define re register 13 #define LL long long 14 #define ULL unsigned long long 15 using namespace std; 16 17 template<class T>inline void read(T&x) 18 { 19 char ch=getchar(); 20 while(!isdigit(ch))ch=getchar(); 21 x=ch-'0';ch=getchar(); 22 while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} 23 } 24 int G[55]; 25 template<class T>inline void write(T x) 26 27 { 28 int g=0; 29 do{G[++g]=x%10;x/=10;}while(x); 30 for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar('\n'); 31 } 32 33 double a[500000],m[500000]; 34 int M,Q; 35 vector<double>range; 36 double ans; 37 int main() 38 { 39 cin>>M>>Q; 40 for(re int i=1;i<=M;i++) cin>>a[i],m[i]=a[i]-floor(a[i]); 41 int l,r; 42 while(Q--) 43 { 44 read(l),read(r); 45 range.clear(); 46 ans=0; 47 int zero=0; 48 for(re int i=l;i<=r;i++) if(m[i]) range.push_back(m[i]); else zero++; 49 sort(range.begin(),range.end()); 50 re int li=0,ri=range.size()-1; 51 while(li<=ri) 52 { 53 if(range[li]>0.5&&zero) li--,zero--; 54 else{ 55 ans-=range[li]; 56 // cout<<"ans+="<<range[li]<<endl; 57 } 58 if(range[ri]<=0.5&&zero) ri++,zero--; 59 else{ 60 ans+=1-range[ri]; 61 // cout<<"ans+=1-"<<range[ri]<<endl; 62 } 63 li++; 64 ri--; 65 } 66 67 cout<<fixed<<setprecision(3)<<fabs(ans)<<endl; 68 } 69 return 0; 70 }
提交的时候,忘记去除调试信息……啊啊啊啊啊啊……
当然,这是暴力,10分吧。
正解
观察暴力,可以发现,一段区间的S’只和实数和,下取整和,上取整和有关系
所以我们只要给三种(实数,下取整小数,上取整小数)搞一个前缀和就好。
Code
1 #include<bits/stdc++.h> 2 using namespace std; 3 template<class T>inline void read(T&x) 4 { 5 char ch=getchar(); 6 while(!isdigit(ch))ch=getchar(); 7 x=ch-'0';ch=getchar(); 8 while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} 9 } 10 int G[55]; 11 template<class T>inline void write(T x) 12 13 { 14 int g=0; 15 do{G[++g]=x%10;x/=10;}while(x); 16 for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar('\n'); 17 } 18 int N,q,c[1<<19];double t[1<<19],s[1<<19]; 19 int main(){ 20 scanf("%d%d",&N,&q); 21 for(int i=1;i<=N;i++){ 22 double x; 23 scanf("%lf",&x),s[i]=s[i-1]+x,t[i]=t[i-1]+ceil(x); 24 c[i]=c[i-1]+(floor(x)!=ceil(x)); 25 } 26 while(q--){ 27 int l,r;read(l),read(r); 28 int n=r-l+1>>1,cnt=c[r]-c[l-1]; 29 double tot=s[r]-s[l-1],tt=t[r]-t[l-1];//取出这一部分的和 30 if(tt-min(cnt,n)>tot) tt-=min(cnt,n); 31 else{ 32 int v=min({cnt,n,int(tt-tot+.5-1e-8)}),t=n-v; 33 tt-=v; 34 if(2*n-cnt<t) tt-=t-(2*n-cnt); 35 } 36 printf("%.3lf\n",abs(tt-tot)); 37 } 38 return 0; 39 }
小结
提交时去除调试信息



