启智树提高组day3T1 3479 : A:climb 树
启智树提高组day3T1 3479 : A:climb 树
题目描述
DoubleDuck山是X省的著名旅游景点。这一天,淘淘慕名而来,打算爬到山顶处。
DoubleDuck山的构造是十分特殊的。在这座山上,总共有n个观景台,我们依次标号为1到n,其中1号观景台在山顶处。对于剩下来的第i(i ≥ 2)号观景台,有且仅有一条长度为wi路径连向上方的第fai(fai < i)号观景台。不难发现,这形成了一个树形结构。
每个观景台到山顶都有一定的距离。我们令dep1 = 0,那么,第i号观景台到山顶的距离为depi =depfai + 1。
为了方便人们爬山,在某些观景台处会有一些缆车。如果i处的缆车能够使用,那么人们就能到达所有到山顶距离小于等于depi的观景台j(不管j号观景台的缆车能否被使用),并且这会花费|depi − depj| ∗ k的时间。(不要吐槽为什么相同高度不需要花费时间)。
淘淘每单位时间走过的长度为1。他想知道,对于每一个观景台,最少要花多少时间才能到达山顶。
输入格式
第一行两个整数n,k。
接下来2到n行,每行三个整数fan,w,ban,分别表示第i个观景台连向哪一个观景台,这条路径的长度,以及缆车的使用情况。如果ban为1,说明不能使用,否则可以。
注意,数据保证fa < i。
输出格式
n行n个整数,第i行表示第i号观景台的答案。
样例
climb0.in | climb0.out |
4 3 1 7 1 1 5 0 2 1 0 | 0 7 3 6 |
样例解释
对于第1号观景台,由于它在山顶,答案为1。
对于第2号观景台,缆车不能使用,只能走路径到达山顶。因此答案为7 1。
对于第3号观景台,缆车能够使用。由于路径的长度为5,坐缆车的时间为|1 − 0| ∗ 3 = 3,所以答案为3。
对于第4号观景台,一种方法是直接坐缆车到达山顶,答案为|2 − 0| ∗ 3 = 6。
1.6 样例2
见下发文件。
数据规模
对于所有数据,所有的路径长度均非负,并且所有答案小于等于10的9次方。k为正整数。
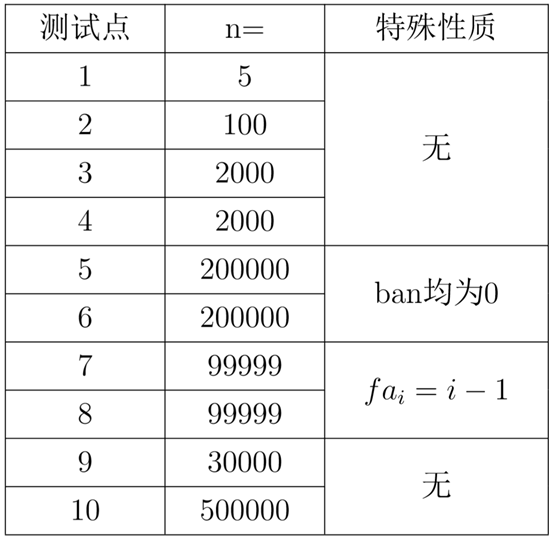
模型描述
很明显这是一颗树,每个观景台都有它唯一的父亲。
其次就先把它转化成链(如task7/8,fai=i-1)
所以可以直接写出方程


