洛谷P4526 【模板】自适应辛普森法2
P4526 【模板】自适应辛普森法2
题目描述
计算积分
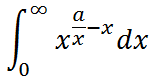
保留至小数点后5位。若积分发散,请输出"orz"。
输入格式
一行,包含一个实数,为a的值
输出格式
一行,积分值或orz
输入输出样例
输入 #1
2.33
输出 #1
1.51068
说明/提示
a<=50
请注意时空限制。
Solution
这和辛普森公式又啥关系?上限可是正无穷!
带着好奇心,我打开了几何画板。
几何画板
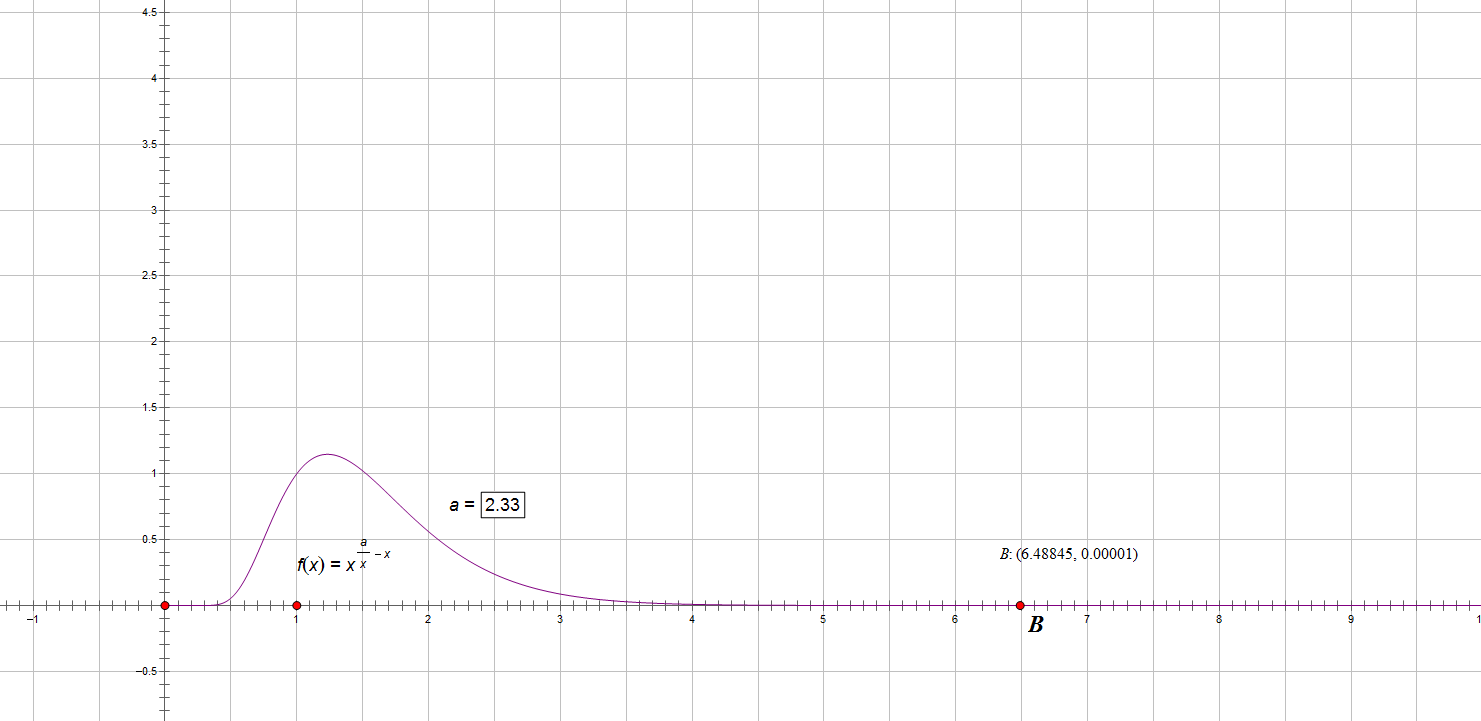
这……这么快就收敛了?!?!?!
看看a=50?
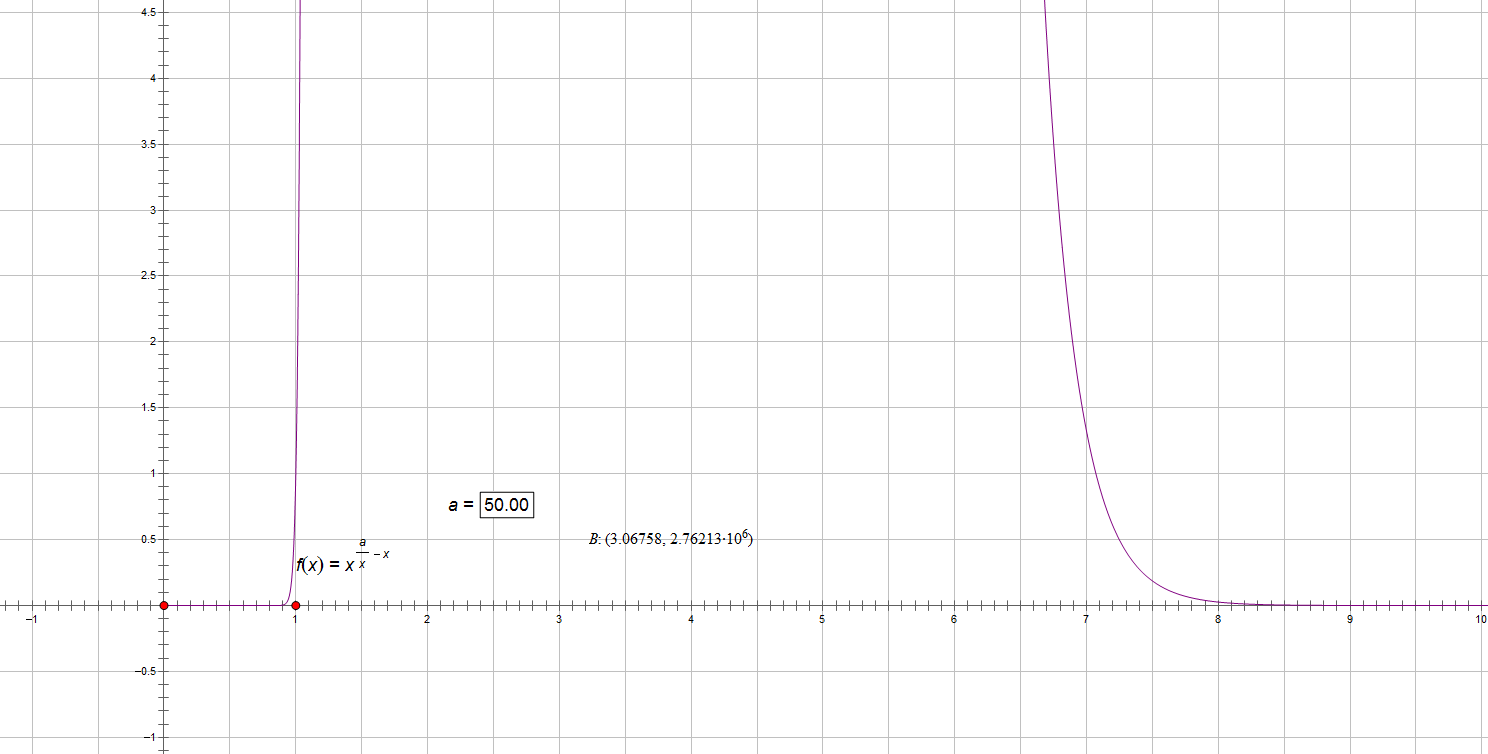
随便把B放在3边上。结果……反正是有限的,有限的就好。
貌似在x=10附近,这玩意就收敛的可怜了……
你有没有考虑a<0?
把B靠近原点,再把a调为-1。
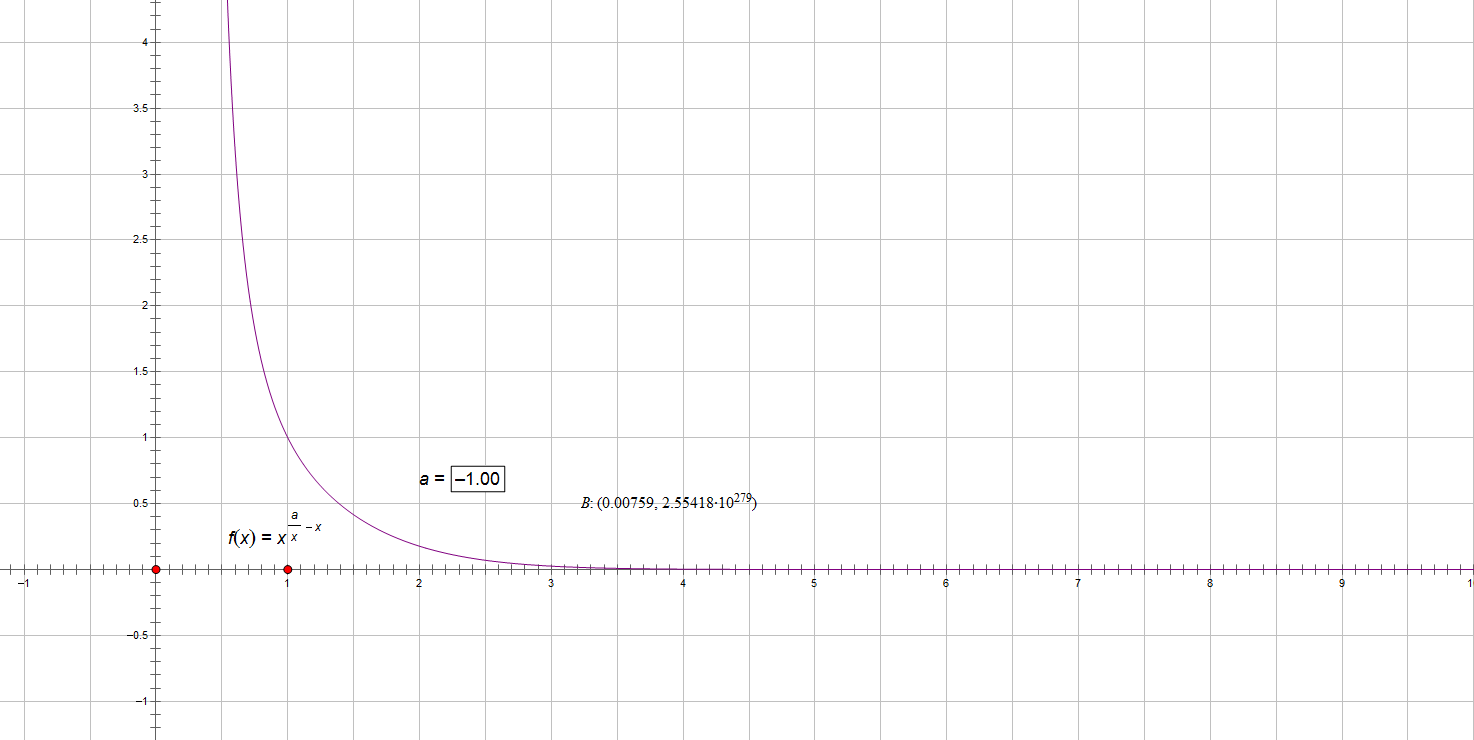
不能想,要是B的横坐标为0会发生什么……貌似直接不显示B点了……
几何画板——自保系统?
从这里就可以得到:
- a<0时函数发散
- a>0时函数收敛于20左右(确保误差尽量小,建议稍大一点)
Code
#include<iostream> #include<cstdio> #include<cmath> #define IL inline #define re register using namespace std; const double eps=1e-12; double a; IL double f(double x) { return pow(x,a/x-x); } IL double simpson(double l,double r) { return (r-l)*(f(l)+4.0*f((l+r)/2.0)+f(r))/6.0; } double integral(double l,double r) { re double mid=(l+r)/2,ans=simpson(l,r); if(fabs(ans-simpson(l,mid)-simpson(mid,r))<eps) return (ans+simpson(l,mid)+simpson(mid,r))/2.0; return integral(l,mid)+integral(mid,r); } int main() { cin>>a; if(a<0) cout<<"orz"; else printf("%.5lf",integral(eps,15)); return 0; }
Attention
保留5位小数

