纪中21日T3 2118. 【2016-12-30普及组模拟】最大公约数

纪中21日T3 2118. 最大公约数

(File IO): input:gcd.in output:gcd.out

时间限制: 1000 ms 空间限制: 262144 KB 具体限制

Goto ProblemSet

题目描述

给出两个正整数A，B，求它们的最大公约数。

输入

第一行一个正整数A。
第二行一个正整数B。

输出

在第一行输出一个整数，表示A，B的最大公约数。

样例输入

18
24

样例输出

数据范围限制

在40%的数据中，1 ≤ A，B ≤ 10^6
在60%的数据中，1 ≤ A，B ≤ 10^18
在80%的数据中，1 ≤ A，B ≤ 10^100
在100%的数据中，1 ≤ A，B ≤ 10^1000

Solution

Algorithm1

正常的gcd（a，b）=gcd（b，a%b）；

开unsigned long long可得六十分（应该不会超时）

Code1

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
unsigned long long gcd(unsigned long long a,unsigned long long b)
{
    return b==0?a:gcd(b,a%b);
}
unsigned long long a,b;
int main()
{
    cin>>a>>b;
    cout<<gcd(a,b);
     return 0;
}

Attention1

函数也要开ULL（缩写）

别把“%”写成“-”，否则在相减前要先使得a>b

而且那样就变成更相减损法了

Algorithm2

gcd二进制法

先看看a，b是不是2的倍数

如果都是，gcd（a，b）=2*gcd（a/2，b/2）；

如果a是，gcd（a，b）=gcd（a/2，b）；

如果b是，gcd（a，b）=gcd（a，b/2）；

如果都不是，gcd（a，b）=gcd（b，a%b）

最后一条=gcd（b，a-b）也可以

（为后面的高精度做铺垫）

Code2

 1 #include<iostream>
 2 #include<iomanip>
 3 #include<algorithm>
 4 #include<cstdio>
 5 #include<cstring>
 6 #include<cmath>
 7 #include<map>
 8 #include<set>
 9 #include<queue>
10 #include<vector>
11 #define IL inline
12 using namespace std;
13 IL unsigned long long gcdbin(unsigned long long a,unsigned long long b)
14 {
15     if(!b) return a;
16     if(!(a|0)&&!(b|0)) return 2*gcdbin(a>>1,b>>1);
17     if(!(a|0)&&(b&1)) return gcdbin(a>>1,b);
18     if((a&1)&&!(b|0)) return gcdbin(a,b>>1);
19     return gcdbin(b,a%b);
20 }
21 unsigned long long a,b;
22 int main()
23 {
24     freopen("rand_gcd.txt","r",stdin);
25     cin>>a>>b;
26     cout<<gcdbin(a,b);
27      return 0;
28 }

Code2

Algorithm3

不压位的高精度

高精度求余数很麻烦（按位求会比较快）

套用更相减损法

同时特判：如果a，b小于19位，依然采用二进制的辗转相除。

Code3

在GMOJ上……

Code3

由于是普通的更相减损，一旦数位超过20使用高精，速度就会很慢很慢很慢……

60分~80分不等

Algorithm4

高精压位

核心算法与Algorithm3相同

Code4

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
const int L=1001;
int a[L],b[L],t[L];
int times=1;
string stra,strb;
bool fail;
IL bool cmp()
{
    for(int i=L-1;i>=0;i--)
    {
        if(a[i]>b[i]) return 0;
        if(a[i]<b[i]) return 1;
    }
    return 0;
}
IL void minus()
{
    
    
} 
IL void diva()
{
    for(int i=L-1;i>=0;i--)
    {
        if(a[i]&1) a[i-1]+=5;
        a[i]>>=1;
    }
}
IL void divb()
{
    for(int i=L-1;i>=0;i--)
    {
        if(b[i]&1) b[i-1]+=5;
        b[i]>>=1;
    }
}
IL void div2()
{
    diva();
    divb();
}
int main()
{
//    freopen("gcd.in","r",stdin);
//    freopen("gcd.out","w",srdout); 
    cin>>stra>>strb;
    for(unsigned int i=0;i<stra.size();i++)
        a[i]=stra[stra.size()-i-1];
    for(unsigned int i=0;i<strb.size();i++)
        b[i]=strb[strb.size()-i-1];
    do{
        if(!(a[0]|0)&&!(b[0]|0)){
            times*=2;
            div2();
            continue;
        }
        if(!(a[0]|0)&&(b[0]&1))
        {
            diva();
            continue;
        }    
        if((a&1)&&!(b|0))
        {
            divb();
            continue;
        }
        
        fail=0;
        for(int i=0;i<L;i++)
        {
            if(a[i]&&b[i])//会不会出现0与非0交错出现呢？概率是(1/10)^L吧…… 
            {
                fail=1; 
                break;
            }
        }
    }while(fail);
    bool zeroa;//为了避免交换，不能确定那个是0 
    for(int i=0;i<L;i++)
    {
        if(a[i]){
            zeroa=0;
            break;
        }
        if(b[i]){
            zeroa=0;
            break;
        }
    }
    bool flag=0;
    if(zeroa)
    for(int i=0;i<L;i++)
    {
        a[i]*=times;
        a[i+1]+=(a[i]>>1)+(a[i]>>3);
        a[i]%=10;
    }
    else
    for(int i=0;i<L;i++)
    {
        b[i]*=times;
        b[i+1]+=(b[i]>>1)+(b[i]>>3);
        b[i]%=10;
    }
    if(zeroa)
    for(int i=L-1;i>=0;i--)
    {
        if(a[i]) flag=1;
        if(flag) cout<<a[i];
    }
    else
    for(int i=L-1;i>=0;i--)
    {
        if(b[i]) flag=1;
        if(flag) cout<<b[i];
    }
    
    
     return 0;
}

Code4

Algorithm5

通过下面（最下面）的对拍发现，四种算法中，二进更相比普通更相更快（不是只有0.3毫秒么？）

高精（可以不压位）二进制更相减损术也不是很难打（而且判断也很快）

Algorithm6

之前是苦于没有时间打高精，终于在今天（2019-11-05 现在是00:17:29），我无意中点开了这篇题解，将我的高精度（甚至都没有压位）的模板稍作修改后边送上了“断头台”……

哈哈哈！

惊到我了！

Code6

由于是模板，所以代码较长。

  1 #include<iostream>
  2 #include<cstring>
  3 #include<cstdio>
  4 #include<cmath>
  5 using namespace std;
  6 
  7 bool insigma(char ch){
  8     return ch=='-'||('0'<=ch&&ch<='9');
  9 }
 10 
 11 const int maxn = 1000;
 12 struct number{
 13     int num[maxn];
 14     int len;
 15     bool fu;
 16     
 17     number(){//初始化 
 18         len=fu=0;
 19         memset(num,0,sizeof(num));
 20     }
 21     
 22     int updata_len(){//更新长度 
 23         for(int i=maxn-1;i>=0;i--) if(num[i]) return len=i+1;
 24         return len=0;
 25     }
 26     
 27     //    /*
 28     number operator= (int x){//隐式转换 
 29         fu=(x<0);
 30         num[0]=abs(x);
 31         if(x>9) carry_bit();
 32         if(x<-9) back_space();
 33         return *this;
 34     }
 35 //    */
 36     /*
 37     number (int x){//有bug的构造函数 暂时用重载=替代 
 38         fu=(x<0);
 39         num[0]=abs(x);
 40         if(x>9) carry_bit();
 41         if(x<-9) back_space();
 42     }
 43     */
 44     
 45     void input(){
 46 //        /*
 47         string a;
 48         cin>>a;
 49         if(a[0]=='-'){
 50             fu=1;
 51             len=a.size()-1;
 52             for(unsigned int i=0;i<a.size()-1;i++) num[i]=a[a.size()-i-1]-'0';
 53         }
 54         else{
 55             len=a.size();
 56             for(unsigned int i=0;i<a.size();i++)    num[i]=a[a.size()-i-1]-'0';
 57         }
 58         
 59 //        */
 60         /*
 61         len=0;
 62         char ch;
 63         while(!insigma(ch=getchar()));
 64         if(ch=='-')
 65             fu=true;
 66         else 
 67             num[len++]=ch-'0';
 68         while(isdigit(ch=getchar())){
 69             num[len++]=ch-'0';
 70         }
 71         int t;
 72         for(int i=0;i<len;i++)
 73         {
 74             t=num[i];
 75             num[i]=num[len-i-1];
 76             num[len-i-1]=t; 
 77         }
 78         */
 79     }
 80     
 81     void output(){
 82         if(fu) cout<<"-";
 83         bool flag=0;
 84         for(int i=len;i>0;i--){
 85             if(num[i]) flag=1;
 86             if(num[i]>9) carry_bit(); 
 87             if(flag) putchar(num[i]+'0');//putchar加速 
 88         }
 89         putchar(num[0]+'0');
 90     }
 91     
 92     friend istream & operator>> (istream &in, number &obj);    
 93     friend ostream & operator<< (ostream &out, number &obj);
 94     
 95     int compare(number x){//2=    1> 0<
 96         if(fu^x.fu){
 97             if(fu) return 0; 
 98             else return 1;
 99         }
100         for(int i=max(len,x.len);i>=0;i--)
101         {
102             if(num[i]>x.num[i]) return !fu;//大于 (1)
103             if(num[i]<x.num[i]) return fu;//小于 (0)
104         }
105         return 2;//相等 
106     }
107     
108     //利用compare()重载比较运算符 
109      
110     bool operator> (number x){
111         return (compare(x)==1);
112     } 
113     
114     bool operator< (number x){
115         return (compare(x)==0);
116     }
117     
118     bool operator>= (number x){
119         return !(*this<x);
120     }
121     
122     bool operator<= (number x){
123         return !(*this>x);
124     }
125     
126     bool operator== (number x){
127         return compare(x)==2;
128     }
129     
130     bool operator!= (number x){
131         return compare(x)!=2;
132     }
133 
134     number operator++ (){
135         num[0]++;
136         if(num[0]>9) carry_bit();
137         return *this;
138     }
139     
140     number operator++ (int){
141         number save=*this;
142         ++*this;
143         return save;
144     }
145     
146     number operator-- (){
147         num[0]--;
148         if(num[0]<0) back_space();
149         return *this;
150     }
151     
152     number operator-- (int){
153         number save=*this;
154         num[0]--;
155         if(num[0]<0) back_space();
156         return save;
157     }
158     
159     bool judge_zero(){
160         for(int i=maxn-1;i>=0;i--)
161             if(num[i]) return 0;
162         return 1;
163     }
164     
165     bool judge_non_zero(){
166         return !judge_zero();
167     }
168     
169     bool convert_bool(){
170         return !judge_zero();
171     }
172     
173     bool even(){
174         if(num[0]%2) return 0;
175         return 1;
176     }
177     
178     bool odd(){
179         if(num[0]%2) return 1;
180         return 0;
181     }
182     
183     void carry_bit(){
184         for(int i=0;i<maxn;i++){
185             num[i+1]+=num[i]/10;
186             num[i]%=10;
187         }
188         updata_len();
189     }
190     
191     void back_space(){
192         for(int i=0;i<maxn;i++){
193             while(num[i]<0) num[i]+=10,num[i+1]--;
194         }
195     }
196     
197     number operator+ (int x){
198         number newness=*this;
199         newness.num[0]+=x;
200         if(newness.num[0]>9) newness.carry_bit();
201         return newness;
202     }
203     
204     number operator+ (number x){
205         number res=x;
206         for(int i=0;i<maxn;i++)
207         {
208             res.num[i]+=num[i];
209         }
210         res.carry_bit();
211         return res;
212     }
213     
214     number operator+= (int x){
215         *this=(*this+x);
216         return *this;
217     }
218     
219     number operator+= (number x){
220         *this=*this+x;
221         return *this;
222     }
223     
224     number operator- (number x){
225         number i,j;
226         if(compare(x)) {i=*this,j=x;}
227         else {i=x,j=*this;}
228         for(int t=0;t<maxn;t++)
229         {
230             i.num[t]-=j.num[t];
231         }
232         i.back_space();
233         return i;
234     }
235     
236     number operator-= (number x){
237         *this=*this-x;
238         return *this; 
239     }
240     
241     number operator* (number x){
242         number sum;
243         sum.fu=fu^x.fu;
244         for(int i=0;i<updata_len();i++)
245         for(int j=0;j<x.updata_len();j++)
246         {
247             if(i+j>maxn-1) continue;
248             sum.num[i+j]+=num[i]*x.num[j];
249         }
250         sum.carry_bit();
251         return sum;
252     }
253     
254     number operator*= (number x){
255         return *this=*this*x;
256     }
257     
258     number factor(){
259         number ans,t;
260         t.num[0]=1;
261         ans.num[0]=1;
262         for(;t<=*this;t.num[0]+=1,t.carry_bit())
263             ans*=t;
264         return ans;
265     }
266     
267     number division2(){
268         for(int i=maxn-1;i>=0;i--){
269             if(num[i]&1&&i!=0) num[i-1]+=10;
270             num[i]>>=1;
271         }
272         return *this;
273     }
274 };
275 
276 istream & operator>> (istream &in, number &obj)
277 {
278     string a;
279     in>>a;
280     if(a[0]=='-'){
281         obj.fu=1;
282         obj.len=a.size()-1;
283         for(unsigned int i=0;i<a.size()-1;i++) obj.num[i]=a[a.size()-i-1]-'0';
284     }
285     else{
286         obj.len=a.size();
287         for(unsigned int i=0;i<a.size();i++) obj.num[i]=a[a.size()-i-1]-'0';
288     }
289     if (!in) obj = number();
290     return in;
291 }
292 
293 ostream & operator<< (ostream &out, number &obj)
294 {
295     if(obj.fu) cout<<"-";
296         bool flag=0;
297         for(int i=obj.len;i>0;i--){
298             if(obj.num[i]) flag=1;
299             if(obj.num[i]>9) obj.carry_bit(); 
300             if(flag) out<<obj.num[i]; 
301         }
302         out<<obj.num[0];
303     return out;
304 }
305 
306 
307 number gcd_rec(number a,number b){
308     if(b.judge_zero()) return a;
309     return gcd_rec(b,a-b);
310 }
311 
312 number gcd(number a,number b){
313     if(a.judge_zero()) return a;
314     number t;
315     for(;;t=b,b=a-b,a=t)
316         if(b.judge_zero()) return a;
317     return a;
318 }
319 
320 number power(number a,number n){
321     number zero;
322     number c;c=1;
323     for(;n>zero;n.division2(),a*=a) if(n.odd()) c*=a;
324     return c;
325 }
326 
327 int main()
328 {
329     freopen("gcd.in","r",stdin);
330     freopen("gcd.out","w",stdout);
331     number a,b,c;
332     cin>>a>>b;
333     c=gcd(a,b);
334     cout<<c;
335     return 0;
336 }

Impression

如果你有兴趣……

#pragma GCC optimize(2)
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
unsigned long long gcd(unsigned long long a,unsigned long long b)
{
    return b==0?a:gcd(b,a%b);
}
unsigned long long a,b;
int main()
{
    freopen("rand_gcd.txt","r",stdin);
    cin>>a>>b;
    cout<<gcd(a,b);
     return 0;
}

gcd.cpp

#pragma GCC optimize(2)
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
unsigned long long gx(unsigned long long a,unsigned long long b)
{
    if(a<b) swap(a,b);
    return b==0?a:gx(b,a-b);
}
unsigned long long a,b;
int main()
{
    freopen("rand_gcd.txt","r",stdin);
    cin>>a>>b;
    cout<<gx(a,b);
     return 0;
}

gx.cpp

#pragma GCC optimize(2)
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
IL unsigned long long gcdbin(unsigned long long a,unsigned long long b)
{
    if(!b) return a;
    if(!(a|0)&&!(b|0)) return 2*gcdbin(a>>1,b>>1);
    if(!(a|0)&&(b&1)) return gcdbin(a>>1,b);
    if((a&1)&&!(b|0)) return gcdbin(a,b>>1);
    return gcdbin(b,a%b);
}
unsigned long long a,b;
int main()
{
    freopen("rand_gcd.txt","r",stdin);
    cin>>a>>b;
    cout<<gcdbin(a,b);
     return 0;
}

gcdbin

#pragma GCC optimize(2)
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
IL unsigned long long gxbin(unsigned long long a,unsigned long long b)
{
    if(!b) return a;
    if(!(a|0)&&!(b|0)) return 2*gxbin(a>>1,b>>1);
    if(!(a|0)&&(b&1)) return gxbin(a>>1,b);
    if((a&1)&&!(b|0)) return gxbin(a,b>>1);
    if(a<b) swap(a,b);
    return gxbin(b,a%b);
}
unsigned long long a,b;
int main()
{
    freopen("rand_gcd.txt","r",stdin);
    cin>>a>>b;
    cout<<gxbin(a,b);
     return 0;
}

gxbin.cpp

#pragma GCC optimize(2)
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<windows.h>
#include<ctime>
#define IL inline
using namespace std;
int main()
{
    freopen("rand_gcd.txt","w",stdout);
    srand(time(NULL));
    cout<<(unsigned long long)rand()*rand()*rand()<<endl;
    cout<<(unsigned long long)rand()*rand()*rand()<<endl;
     return 0;
}

rand_gcd.cpp

#pragma GCC optimize(2)
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<ctime>
#define IL inline
using namespace std;
int avg[4];
int times;
int main()
{
    system("random_gcd.exe");
    int s1=clock();
    system("gcd.exe");
    int s2=clock();
    system("gcdbin.exe");
    int s3=clock();
    system("gx.exe");
    int s4=clock();
    system("gxbin.exe");
    int e=clock();
//    cout<<"\n辗转相除："<<s2-s1<<"ms\n";
//    cout<<"二进辗转："<<s3-s2<<"ms\n";
//    cout<<"更相减损："<<s4-s3<<"ms\n"; 
//    cout<<"二进更相："<<e-s4<<"ms\n";
    avg[0]+=s2-s1;
    avg[1]+=s3-s2;
    avg[2]+=s4-s3;
    avg[3]+=e-s4;
    times++;
    if(times>=100)
    {
        system("cls");
        cout<<"总计"<<times<<"组数据\n"; 
        cout<<"平均用时：\n"; 
        cout<<"辗转相除："<<avg[0]/(times*1.0)<<"ms\n";
        cout<<"二进辗转："<<avg[1]/(times*1.0)<<"ms\n";
        cout<<"更相减损："<<avg[2]/(times*1.0)<<"ms\n"; 
        cout<<"二进更相："<<avg[3]/(times*1.0)<<"ms\n";
        return 0;
    }
    main(); 
     return 0;
}

gcd对拍.cpp

1000组数据运算结果如下

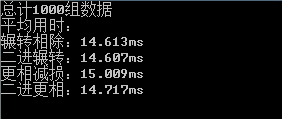
End

posted @ 2019-08-21 16:49 Vanilla_chan 阅读(388) 评论(0) 编辑收藏举报

刷新页面返回顶部

折柳

纪中21日T3 2118. 【2016-12-30普及组模拟】最大公约数

纪中21日T3 2118. 最大公约数

题目描述

输入

输出

样例输入

样例输出

数据范围限制

Solution

Algorithm1

Code1

Attention1

Algorithm2

Code2

Algorithm3

Code3

Algorithm4

Code4

Algorithm5

Algorithm6

Code6

Impression

公告