纪中10日T1 2300. 【noip普及组第一题】模板题

2300. 【noip普及组第一题】模板题 

(File IO): input:template.in output:template.out

时间限制: 1000 ms  空间限制: 262144 KB  具体限制  

题目描述

 

输入

 

输出

样例输入

 

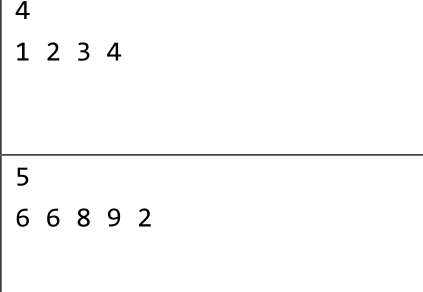
样例输出

 

数据范围限制

 

朴素算法

考试开始的前一个小时我一直在折腾朴素算法 -> 对拍

 1 #pragma GCC optimize(2)
 2 #include<bits/stdc++.h>
 3 #define IL inline
 4 using namespace std;
 5 int a[100001];
 6 bool vis[100001];
 7 int n,k,maxans;
 8 bool cmp(int a,int b)
 9 {
10     return a>b;
11 }
12 int gcd(int a,int b)
13 {
14     if(b==0) return a;
15     if(b==1) return 1;
16     if(a%2==0&&b%2==0) return 2*gcd(a/2,b/2);
17     if(a%2==1&&b%2==0) return gcd(a,b/2);
18     if(a%2==0&&b%2==1) return gcd(a/2,b);
19     if(a%2==1&&b%2==1) return gcd(b,a%b);
20 //    return (b==0)?a:gcd(b,a%b);
21 //这里还用到了二进制gcd（会更快一点）
22 }
23 void search(int depth/*k*/,int now)
24 {
25     if(depth==k) {
26         maxans=max(maxans,now);
27         return;
28     }
29     int maxgcd=0,maxnum=0;
30     for(int i=1;i<=n;i++)
31     {
32         if(vis[i]) continue;
33         if(gcd(now,a[i])>maxgcd){
34             maxnum=i;
35             maxgcd=gcd(now,a[i]);
36             if(depth+1<k){
37                 vis[i]=1;
38                 search(depth+1,maxgcd);
39                 vis[i]=0;
40             }
41         }    
42         if(depth+1==k)
43         {
44             vis[i]=1;
45             search(depth+1,maxgcd);
46             vis[i]=0;    
47         }
48     }
49 }
50 int main()
51 {
52     freopen("template.in","r",stdin);
53     freopen("template.out","w",stdout);
54     cin>>n;
55     for(int i=1;i<=n;i++)
56         scanf("%d",a+i);
57     sort(a+1,a+n+1,cmp);
58     for(k=1;k<=n;k++)
59     {
60         if(a[k]==1){
61             printf("1\n");
62             continue;
63         }
64         maxans=0;
65         for(int s=1;s<=n;s++)
66         {
67             vis[s]=1;
68             search(1,a[s]);
69             vis[s]=0;
70         }
71         printf("%d\n",maxans);
72     }
73     return 0;
74 }
我再也不想看到了

这个算法就是模拟，谁都会写吧？

O（n2）算法

我会写出这个算法来，完全是因为下面的那一种在考试时我写出来有问题

Solution

 先在输入的同时预处理出每个数的所有因数（可以是质数，合数，也可以是1）

for(int j=1;j<a;j++)
    if(a%j==0)
        array[j]++;

这样子的好处是，我没有保存每一个数，而是统计了所有的因子

这里的array[i]就表示因子有i的数有多少个

于是我们要计算 10,000个数 * 10,000个可能的因子 次询问

哈哈

还是把这种讲完吧

然后再外层循环k++

内层循环i--

一旦有一个array[i]>=k

就把这时的i输出即可

Code（TLE70分）

 1 //#pragma GCC optimize(2)
 2 #include<bits/stdc++.h>
 3 using namespace std;
 4 int array[100001];
 5 int a,n,k,maxa;
 6 int main()
 7 {
 8     freopen("template.in","r",stdin);
 9     freopen("template.out","w",stdout);
10     cin>>n;
11     for(int i=1;i<=n;i++){
12         scanf("%d",&a);
13                 for(int j=1;j<a;j++)
14                         if(a%j==0)
15                 array[j]++;
16                 maxa=max(maxa,a);
17     }
18     int b=maxa;
19     for(k=1;k<=n;k++)
20     {
21         for(int i=b;i>0;i--)
22         {
23             if(array[i]>=k){
24                 cout<<i<<endl;
25                 b=i;
26                 break;
27             }
28         }
29     }
30     return 0;
31 }
Code（TLE70分）

O（n sqrt（n））算法

Solution

 

posted @ 2019-08-10 19:52  Vanilla_chan  阅读(274)  评论(0)  编辑  收藏  举报