嵊州集训小结
嵊州集训小结
以下是2019年7月11~17日,我在嵊州市嵊州中学机房里,东塔路惠余宾馆里的部分付出与收获。
0x00 搜索优化
(普通搜索:老师觉得太简单就没有讲,一句带过了。其实DFS,BFS也没有什么难度的啦!)
引入:
在模拟赛中,我们总是要用到搜索,而DFS和BFS各有各的优缺点,常常还没搜到,就会TLE/MLE。
而且,有些数据则会专门针对有些简单的算法出一些比较偏/深的数据,使我们得不到分。
所以,仅仅掌握普通搜索是不够的!
0x01 双向宽搜
定义:宽度优先搜索(BFS)沿起点到终点,终点到起点的搜索
条件:1、操作可逆 2、已知目标状态
优点:省时间省空间
效率:普通BFS的2/(kx/2+1)。(有x层的完全k叉树)
例题1:最少点路径(minpoint)
在一个无向图中求经过最少点的从S到T的路径。
solution1:用一个一位数组,[0]放S,[inf]放T。起点终点同时搜索。
例题2:分油问题
0x02 迭代加深(DFS-ID)
定义:从小到大限制搜索的深度,如果在当前深度限制下搜不到答案,就把深度限制增加,重新进行一次搜索。
优点:继承了DFS比BFS省空间的特点,也没有需要很大的空间。
条件:1、搜索树规模随层次增长很快 2、能确保答案在一个较浅的节点
效率:虽然当搜索限制d层时,我们要先再搜索第1~d-1层的节点,但当树节点的分支节点数目较多时,每层的节点数会呈指数级增长。这与普通DFS搜索的深层子树规模相比,也是微不足道了。
例题1:小猫爬山 cat
有N只猫要乘坐一次一元,最大承载量为W的缆车。已知每只猫的数量,求最少花多少钱
solution1:1、从大到小排列 2、肥猫先上车,瘦猫后上车 3、穷举(二分也可以,且当N大时,二分更快)
0x02.5 计算完全k叉树的节点个数
设此树是有d层的完全k叉树
则节点个数为:
1+k+k^2+k^3+k^4+……+k^d=(k^(d+1)-1)/(k-1)
即:
1+k+k2+k3+k4+……+kd=(kd+1-1)/(k-1)
(等比数列求和公式)
0x03 记忆化搜索
目的:避免重复搜索同一个节点
结构:DFS递归
思想:相当于DP,但当拓扑关系复杂时,DP不可用
模型:

1 int work(int s) 2 { 3 if(ops[s]/*已经计算过了*/) 4 { 5 work=opt[s]; 6 return 0; 7 } 8 else 9 for(/*枚举所有可以推导出状态的s的状态(前驱)*/) 10 { 11 int tmp=/*由s1推出的最优值*/; 12 if(opt(s)/*未计算过*/||tmp/*优于opt[s]*/) 13 /*更新opt[s]为最优值*/; 14 } 15 }
例题1:巧克力 chocolate
有个矩形cho,n行m列,n*m个大小相同的小块……
练习1:函数运行乐趣 Function Run Fun
http://acm.hdu.edu.cn/showproblem.php?pid=1579
洛谷https://www.luogu.org/problem/P1464
我的题解https://www.cnblogs.com/send-off-a-friend/p/11352031.html

1 #include<bits/stdc++.h> 2 using namespace std; 3 int a,b,c,ra,rb,rc; 4 int memory[21][21][21]={}; 5 long long w(int a,int b,int c) 6 { 7 if(a<=0||b<=0||c<=0){ 8 return 1; 9 } 10 if(a>20||b>20||c>20){ 11 return w(20,20,20); 12 } 13 if(memory[a][b][c]!=-1) return memory[a][b][c]; 14 if(a<b&&b<c){ 15 return memory[a][b][c]=w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c); 16 } 17 return memory[a][b][c]=w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1); 18 } 19 int main() 20 { 21 memset(memory,-1,sizeof(memory)); 22 cin>>a>>b>>c; 23 while(a!=-1||b!=-1||c!=-1){ 24 int ans=w(a,b,c); 25 printf("w(%d, %d, %d) = %d\n",a,b,c,ans); 26 // memory[a][b][c]=ans; 27 cin>>a>>b>>c; 28 } 29 return 0; 30 }
0x04 状态表示和状态压缩(及HASH表)
定义:把当前的状态特殊处理,使状态表示更简单
优点:能充分的反应关系,以及省空间
应用1:八皇后问题
solution1:位运算压缩
使用递归&三个参数row,ld,rd 分别代表竖线,左下斜对角线,右下斜对角线,表示纵列和双对角线方向限制
以6*6为例
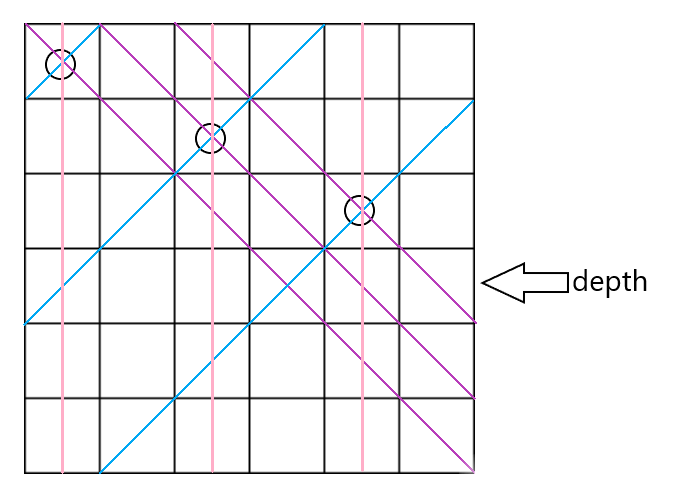
如图,此时
depth=4
row=101010(14)
ld=100100(36)
rd=000111(7)
那么
这一行的状态就是:
now = row | ld | rd
边界检测:
如果now = 1 << 6-1 //1000000-1=111111
return 0;
递归调用:
将row不变,ld左移一位,rd右移一位
即:work(row,ld << 1,rd >> 1);
完成情况:
depth==n+1
此时,输出。

1 #include<iostream> 2 #define IL inline 3 using namespace std; 4 int n,ans,jf; 5 int queen[20]; 6 IL void dfs(int depth,int ld,int rd,int row) 7 { 8 int now=ld|rd|row; 9 if(depth>=n){ 10 if(++jf<=3){ 11 for(int i=0;i<n;i++)cout<<queen[i]+1<<" "; 12 cout<<endl; 13 } 14 ans++; 15 return; 16 } 17 for(int i=0;i<n;i++) 18 { 19 if((now>>i)&1) continue; 20 queen[depth]=i; 21 ld^=1<<i;rd^=1<<i;row^=1<<i; 22 dfs(depth+1,ld<<1,rd>>1,row); 23 ld^=1<<i;rd^=1<<i;row^=1<<i; 24 queen[depth]=0; 25 } 26 } 27 int main() 28 { 29 cin>>n; 30 dfs(0,0,0,0); 31 cout<<ans; 32 return 0; 33 }
应用2:八数码问题
压缩成一个九位数
(双向宽搜)
0x04 搜索剪枝
相当于排除死胡同
原则:A.正确性 B.准确性 C.高效性
0x04.1 可行性剪枝
“从当前状态可得解吗?”
例题1:门票 tecket
用c个字母(都已知),组成长度为L的字符串。
3<=L<=15 至少一个元音字母,两个辅音字母。按字母序输出。
solution:剪枝
1、对a[c]排序
2、预处理:用b[i]表示a中[i]后还有几个元音
3、递归深搜:dfs(int x,int y,int n1,int n2,string s)
//搜到第x个字符,已经生成了y长度的字符串
//至少还要n1个元音,n2个辅音,生成的字符串为s
if(len+1==y) {cout<<s;计数器+1;}
else{if(a[i]是元音} dfs(x+1,y+1,n1-1,n2,s+a[x]);
else dfs(x+1,y+1,n1,n2-1;s+a[x]);
剪枝:
1、接下来字母全用也不够
总数-x<len-(y-1)
2、接下来无元音,且之前没有用元音
len-y<n1&&b[x+1]<n1
3、接下来辅音全用长度也不够
自己试着写一下吧~
应用2:Betsy的旅行
一个N2的小镇被分成N*N个格子
Betsy从左上走到左下,每个格子恰好经过一次。
给定N(N<=7),有多少种?
solution2:剪枝
不能单纯的扫描全局(那样是O(N2))
分析发现
Betsy移动只影响其周边格子
1、不能形成空格子(四边全封闭)
可以检测现在的位置的上下左右格来实现
2、留给你自己想啦~
剪枝就是要开动脑筋嘛!
0x04.2 最优化剪枝
方法:保存一个“当前最优解”——解的优度下限(用估价函数h())
例题1:快速加 quicksum
比如:12 & 3
0次:12
1次:1+2=3 √
再比如:303 & 6
0次:303
1次:3+03=6 √ 或30+3=33
2次:3+0+3=6 × (非最优解)
(这也说明可以有前导0)
solution1:
算法1:DP模型(石子合并)
暂时先不考虑
算法2:S+TBJ
用g[i][j]表示si->sj的值
dfs(i,last,p,sum);
边界:得到答案
if(i==len)//形成了结果
{
sum+=g[last][len];
if(sum==n)
if(p<ans) ans=p;
}
剪枝:
1、当前sum+剩下不加加号组成的数小于n
2、当前sun>n
3、已加加号数p大于最优解ans
(2019-07-17 22:43:20)
例题2:特别的数列 seq
数列A1,A2,An.
0x10 图论相关
图的定义:由点,边构成的模型
分为有向图和无向图
储存结构
1、二维数组(邻接矩阵)几乎不需要预处理
2、邻接表(3*一维数组) 预处理特别快,方便排序,统计出边
3、邻接链表(点|权|指针)(vector|map) 也可用数组模拟,可以快速访问一条边的反向边
0x11 Prim
用来计算最小生成树(MST,Minimum Spanning Tree)
基于贪心
用邻接表存储边(结构体更好)
- 从任意一点开始
- 扫描MST所有出边,选用离当前MST距离(边权)最小的点加入MST(即优先用边权小的边)
- 标记此点(用bool数组)
暴力O(|v|2)
堆优化后O(|v|*log(|v|))
0x05 kruskal
克鲁斯卡尔
基于贪心
同Prim,用来计算最小生成树(MST,Minimum Spanning Tree)
用并查集来查看是否形成环
- 使用邻接表储存两点之间的边权
- 将所有边按照边权进行排序(从小到大)
- 每次选取最小边权的两点,查询这两点是否在同一集合内
- 若不在,则将这两点连接,使用并查集并merge(合并)这两点
- 重复3,4直到连了n-1条边(或只有一个点的祖先是自己),即所有点都在同一个连通分量中
平均时间复杂度为O(|E|log|E|),其中E和V分别是图的边集和点集。(百度百科)



