2017提高组D1T1 洛谷P3951 小凯的疑惑

洛谷P3951 小凯的疑惑 

原题

题目描述

小凯手中有两种面值的金币，两种面值均为正整数且彼此互素。每种金币小凯都有 无数个。在不找零的情况下，仅凭这两种金币，有些物品他是无法准确支付的。现在小 凯想知道在无法准确支付的物品中，最贵的价值是多少金币？注意：输入数据保证存在 小凯无法准确支付的商品。

输入输出格式

输入格式：

 

两个正整数 a 和 b，它们之间用一个空格隔开，表示小凯中金币的面值。

 

输出格式：

 

一个正整数 N，表示不找零的情况下，小凯用手中的金币不能准确支付的最贵的物品的价值。

 

输入输出样例

输入样例#1： 

3 7

输出样例#1： 

11

说明

【输入输出样例 1 说明】

小凯手中有面值为3和7的金币无数个，在不找零的前提下无法准确支付价值为1,2,4,5,8,11 的物品，其中最贵的物品价值为 11，比11 贵的物品都能买到，比如：

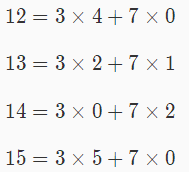
【数据范围与约定】

 

 

---

小学奥数法

运用公式a*x+b*y=k，max(k)=a*b-a-b

我对小奥一窍不通，更别说什么同余那些东西了

我的理解：假设两种钱每种最少要拿一次（也就是不能不拿），不能凑成的最小钱数为k，因为a和b互质，显然,k = a * b，(当k = a * b 时，由于ab互质，要么a拿b个，要么b拿a个)。 由于a和b可以一样都不拿，所以ans = k - a - b = a * b - a - b吧。。。

感觉貌似有那么点道理

2019-07-16 21:05:54更新

今天我在回顾博客园时，问了大佬一个问题：我写的对了吗？

突然自己都发现有问题

原本的题解，貌似是当时看懂了一位大佬后，照搬过来的呢。。。

有点bug，比如说k的定义？

不能凑成的最小钱数为k

既然不能凑成，那么哪来的k=a*b？

所以，旧东西有些是要检查，然后舍弃的呢！

看看能不能开学后问问老板吧

更新完毕

不过还是看具体公式推导吧

其实，这道题目是一道数学定理——赛瓦维斯特定理：已知a,b为大于1的正整数，(a,b)=1,则使不定方程ax+by=Cax+by=C无负整数解的最大整数C=ab−a−bC=ab−a−b！

证明：
若存在x,y>=0x,y>=0满足 ax+by=ab−a−bax+by=ab−a−b 则a(x+1)+b(y+1)=aba(x+1)+b(y+1)=ab
于是a|(y+1)a|(y+1),b|(x+1)b|(x+1)
(a(x+1)=b(a−y−1)a(x+1)=b(a−y−1)，有 a,b互质，所以b|(x+1)b|(x+1)。a|(y+1)a|(y+1)同理）
又x+1>=1,y+1>=1x+1>=1,y+1>=1
故a(x+1)+b(y+1)>=a∗b+b∗a=2aba(x+1)+b(y+1)>=a∗b+b∗a=2ab (因为b|(x+1)b|(x+1),所以b<=x+1b<=x+1,同理a<=y+1a<=y+1)
但是在上述假设中我们知道a(x+1)+b(y+1)=aba(x+1)+b(y+1)=ab,a>=0,b>=0a>=0,b>=0
所以假设不成立，即不存在x,y>=0x,y>=0,满足 ax+by=ab−a−bax+by=ab−a−b
 
对于任意正整数C>=ab−a−b+1C>=ab−a−b+1，即C+a+b>=ab+1C+a+b>=ab+1
设C+a+b=ka+m(k>=b,1<=m<=a−1)C+a+b=ka+m(k>=b,1<=m<=a−1)
注意到(a,b)=1
由裴蜀定理，知存在x0,y0∈Zx0,y0∈Z，使得ax0+by0=1ax0+by0=1
故存在x1,y1∈Z，−(b−1)<=x1<=−1x1,y1∈Z，−(b−1)<=x1<=−1
使得ax1+by1=max1+by1=m
(解释一下，这里的意思其实是设−(b−1)<=x1<=−1−(b−1)<=x1<=−1，一定存在整数y1y1使得ax1+by1=max1+by1=m成立。原因就是在整数x1x1的取值中一共有b−1b−1个数，y1=(m−ax1)/by1=(m−ax1)/b，总是可以找到x1x1使得m−ax1m−ax1能被b整除）
显然，y1>=1(ax1<0,m>0,b>0y1>=1(ax1<0,m>0,b>0，因此y1>=1y1>=1)
于是，取x=k+x1−1,y=y1−1x=k+x1−1,y=y1−1
注意到x1,y1x1,y1的取值范围，得x,y>=0x,y>=0
得ax+by=Cax+by=C
所以任意C>=ab−a−b+1C>=ab−a−b+1都存在x,y>=0x,y>=0,ax+by=Cax+by=C
证毕

　　

　代码如下：　

//AC
//luoguP3951小凯的疑惑 
#include<iostream>
using namespace std;
int main()
{
    long long a,b;
    cin>>a>>b;
    cout<<a*b-a-b;
    return 0;
}

 

---

暴力法

简单粗暴的枚举，但是枚举量无疑是巨大的。每个枚举量的最大值都是a*b(根据上面推理的公式，且题目中给出a，b互质，说明结果一定会小于a*b)。逐一舍去可以被表示出来的数字（赋予1），最后再倒序从a*b-1开始输出第一个为零的数字

还有地方需优化

//60分 
//luoguP3951小凯的疑惑  
#include<iostream>
using namespace std;
bool number[100000000000000];
int main()
{
    long long a,b;
    cin>>a>>b;
    for(long long i=0;i*a<a*b;i++)
        for(unsigned long long j=0;j*b<a*b;j++)
        {
            if(i*a+j*b>a*b) break;
            number[i*a+j*b]=1;
        }
    for(long long i=a*b-1;i>0;i--)
        if(number[i]==0) {cout<<i;break;}
    return 0;
    
}

之后，我下载了#13测试数据：66650775 6074462

对应的答案：404867527282813

你就知道为什么会不能通过了——超时

---

第三种方法

被启发 by 我的好室友NLH

因为对于每一个可以得到的商品的价格，再加上a或b，小凯也可以买到。那么每一个数字就有两种选择，直到数字超过了a*b。

不过，想法十分巧妙效果一般

还有地方需改进

//30分
//luoguP3951小凯的疑惑 
#include<iostream>
using namespace std;
unsigned long long a,b;
bool number[1000000000];
void function(unsigned long long one){
    if(one>a*b) return;
    number[one]=1;
    //cout<<one<<endl;//倘若你输出每一次的one值，你就可以看到效率是多么的低。。。
    function(one+a);
    function(one+b);
} 
int main()
{
    cin>>a>>b;
    function(0);
    for(unsigned long long i=a*b-1;i>0;i--)
        if(number[i]==0) {cout<<i;break;}
    return 0;
}

 

---

总结

总而言之，还是第一种方法好，没有任何的循环等等。。。

但它也是最难理解的一种。

做这种题时，要好好想想有没有更简单的方法，其次是数学基本功底要好。

再接再厉！

好的，那就先这么草率的结束了吧！