Mini-batch 梯度下降 与Tensorflow中的应用
mini-batch在深度学习中训练神经网络时经常用到,这是一种梯度下降方法,可以很快的降低cost,接下来系统介绍一下。
1. 什么是 mini-batch梯度下降
先来快速看一下BGD,SGD,MBGD的定义,
当每次是对整个训练集进行梯度下降的时候,就是batch梯度下降
当每次只对一个样本进行梯度下降的时候,就是 stochastic梯度下降
当每次处理样本的个数在上面二者之间,就是mini batch 梯度下降
我们知道batch梯度下降的做法是,在对训练集执行梯度下降算法时,必须处理整个数据集,然后才能进行下一步梯度下降。
在处理完整个训练集之前,先让梯度下降法处理一部分数据,那么算法就相对快一些。
也就是把整个大的训练集划分为若干小的训练集,被成为mini batch
例如 500万 的训练集,划分为每个子集中只有1000个样本,那么一共会有5000个这样的子集。同样的,对y也做相同的划分:
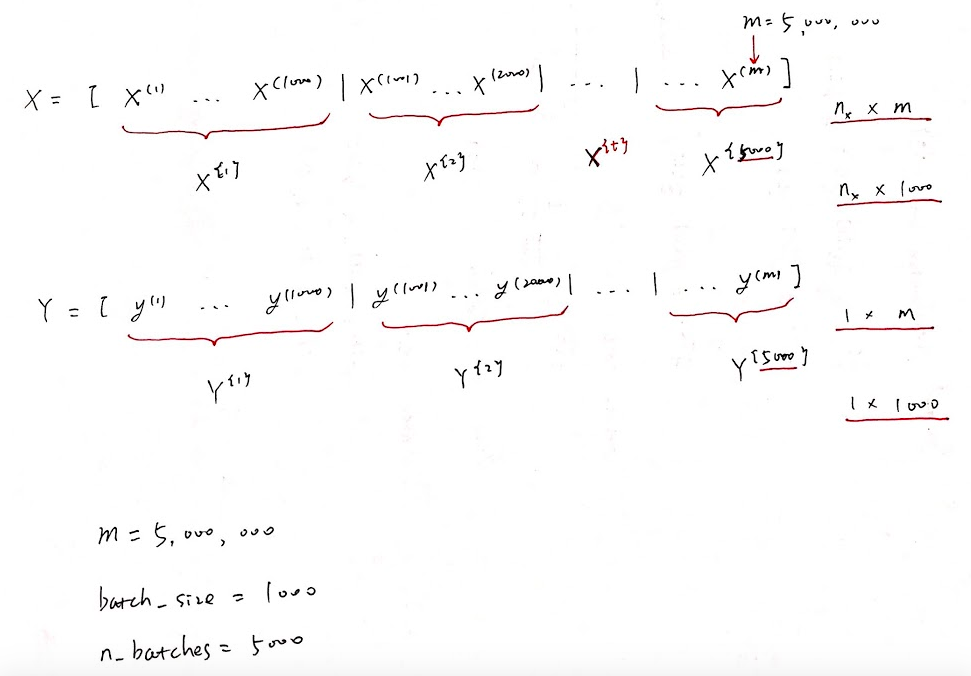
上角标用大括号表示为第几个子集,小括号表示第几个样本,中括号为神经网络的第几层。
这时候,每一次对每个子集进行整体梯度下降,也就是对1000个样本进行整体梯度下降,而不是同时处理500万个x和y。相应的这个循环要执行5000次,因为一共有5000个这样的子集。
2. mini-batch梯度下降具体算法

t代表第几个子集,从1到5000,因为划分后,一共有5000个子集,
1.对每个子集,进行前向计算,从第一层网络到最后一层输出层
因为batch梯度下降是对整个数据集进行处理,所以不需要角标,而mini-batch这里需要对x加上角标,表示是第几个子集。
2.接下来计算当前子集的损失函数,因为子集中一共有1000个样本,所以这里除以1000。损失函数也是有上标的,和第几个子集相对应。
3.然后进行反向传播,计算损失函数J的梯度。
4.最后更新参数。
将5000个子集都计算完时,就是进行了一个epoch处理,一个epoch意思是遍历整个数据集,即5000个子数据集一次,也就是做了5000个梯度下降。
如果需要做多次遍历,就需要对epoch进行循环。当数据集很大的时候,这个方法是经常被使用的。
3. 为什么需要 mini-batch梯度下降
当数据集很大时,训练算法是非常慢的,
和 batch 梯度下降相比,使用mini-batch梯度下降更新参数更快,有利于更鲁棒地收敛,避免局部最优。
和 stochastic 梯度下降相比,使用 mini-batch 梯度下降的计算效率更高,可以帮助快速训练模型。
4. 进一步看batch,stochastic,mini batch 梯度下降的比较
来看一下cost函数随着训练的变化情况:
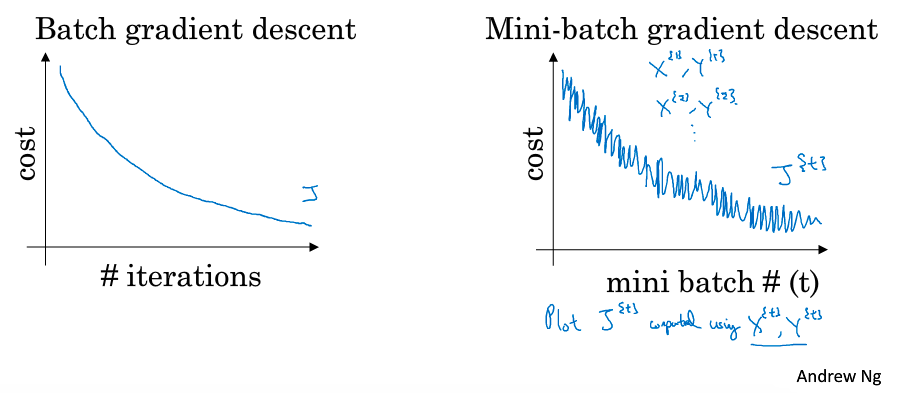
在 batch梯度下降中,单次迭代的成本是会下降的,如果在某次迭代中成本增加了,那就是有问题了。
在 mini batch 梯度下降中,并不是每一批成本都是下降的,因为每次迭代都是训练不同的子集,所以显示在图像上就是,整体走势是下降的,但是会有更多的噪音。
噪音的原因是,如果是比较容易计算的子集,需要的成本就会低一些,遇到难算的子集,成本就会高一些。
图中中间那个点就是想要达到的最优的情况:
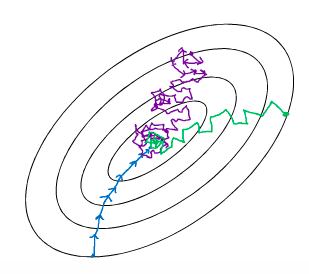
蓝色:为 batch 梯度下降,即 mini batch size = m,
紫色:为 stochastic 梯度下降, 即 mini batch size = 1,
绿色: 为 mini batch 梯度下降, 即 1< mini batch size < m。
Batch gradient descent,噪音小一些,幅度大一些。
BGD的缺点,每次对整个训练集进行处理,那么数量级很大的时候耗费时间就会比较长。
Stochastic gradient descent,因为每次只对一个样本进行梯度下降,所以大部分时间是向最小值靠近的,但也有一些是离最小值越来越远,因为那些样本恰好指向相反的方向。所以看起来会有很多噪音,但整体趋势是向最小值逼近。
但SGD永远不会收敛,它只会在最小值附近不断的波动,不会到达也不会再次停留。
SGD的噪音,可以通过调节学习率来改善,但是它有一个很大的缺点,就是不能通过进行向量化来进行加速,因为每次都知识对一个样本进行处理。
Mini Batch Gradient descent的每个子集的大小刚好位于两种极端情况之间。
那么就有两个好处,一个是可以进行向量化处理,另一个是不用等待整个训练集训练完就可以进行后续的工作。
MBGD的成本函数变化,不会一直朝着最小值的方向前进,但和SGD相比,会更持续的地靠近最小值。
5. 如何选择mini batch的参数 batch size 呢?
不难看出 Mini Batch gradient descent 的batch大小,也是一个影响算法效率的参数。
如果训练集小的话,一般小于2000的,就直接使用 Batch Gradient descent。
一般Mini Batch Gradient Descent 的大小在64到512之间,选择2的n次方会运行的更快一些。
注意这个值设为2的n次幂,是为了符合cpu gpu的内存要求,如果不符合的话,不管用什么算法表现都会很糟糕。
6. 在TensorFlow中应用举例
下面这个例子是对fetch_california_housing数据集 用一个简单的线性回归预测房价,在过程中用到了mini batch 梯度下降:
损失函数用 MSE , 对每个子集 x_batch, y_batch 应用 optimizer = tf.train.GradientDescentOptimizer。
详细注释见代码:(具体代码上传至github了,地址为mini-batch的demo)
# -*-coding:utf-8-*-
# fetch_california_housing 数据集包含9个变量的20640个观测值,
# 目标变量为平均房屋价,
# 特征包括:平均收入、房屋平均年龄、平均房间、平均卧室、人口、平均占用、维度和经度。
import numpy as np
import tensorflow as tf
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing() # 获取放假数据
m, n = housing.data.shape # 获取数据维度,矩阵的行列长度
scalar = StandardScaler() # 将特征进行标准归一化
scaled_housing_data = scalar.fit_transform(housing.data)
scaled_housing_data_plus_bias = np.c_[np.ones((m, 1)), scaled_housing_data] # np.c_是连接的含义,加了一个全为1的列
learning_rate = 0.01
# X 和 y 为placeholder, 后面将要传进来的数据占位
X = tf.placeholder(tf.float32, shape=(None, n+1), name="X") # None 就是没有限制,可以任意长
y = tf.placeholder(tf.float32, shape=(None, 1), name="y")
# 随机生成 theta,形状为(n+1, n),元素在[-1.0, 1.0) 之间
theta = tf.Variable(tf.random_uniform([n+1, 1], -1.0, 1.0, seed=42), name="theta")
# 线性回归模型
y_pred = tf.matmul(X, theta, name="predictions")
# 损失用MSE
error = y_pred - y
mse = tf.reduce_mean(tf.square(error), name="mse")
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(mse)
# 初始化所有向量
init = tf.global_variables_initializer()
n_epochs = 10
# 每一批样本数设为100
batch_size = 100
n_batches = int(np.ceil(m/batch_size)) # 总样本数除以每一批的样本数,得到批的个数,要得到比它大的最近的整数
# 从整批中获取数据
def fetch_batch(epoch, batch_index, batch_size):
np.random.seed(epoch * n_batches + batch_index) # 用于 random,每次可以得到不同的整数
indices = np.random.randint(m, size=batch_size) # 设置随机索引,最大值为m
X_batch = scaled_housing_data_plus_bias[indices]
y_batch = housing.target.reshape(-1, 1)[indices]
return X_batch, y_batch
with tf.Session() as sess:
sess.run(init)
for epoch in range(n_epochs):
for batch_index in range(n_batches):
X_batch, y_batch = fetch_batch(epoch, batch_index, batch_size)
sess.run(training_op, feed_dict={X: X_batch, y:y_batch})
best_theta = theta.eval()
print("Best theta:\n", best_theta)



