机器学习中常用评估指标
评估指标 Evaluation metrics 可以说明模型的性能,辨别模型的结果。
我们建立一个模型后,计算指标,从指标获取反馈,再继续改进模型,直到达到理想的准确度。在预测之前检查模型的准确度至关重要,而不应该建立一个模型后,就直接将模型应用到看不到的数据上。
今天先来简单介绍几种回归和分类常用的评估方法。
回归
均方误差:
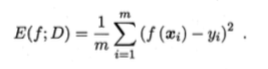
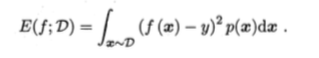
其中D为数据分布,p为概率密度函数。
from sklearn.metrics import mean_squared_error y_true = [3, -0.5, 2, 7] y_pred = [2.5, 0.0, 2, 8] mean_squared_error(y_true, y_pred) 0.375
分类
二分类和多分类:
错误率
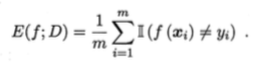
准确率
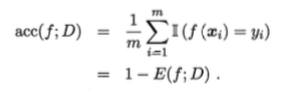
二分类
混淆矩阵:
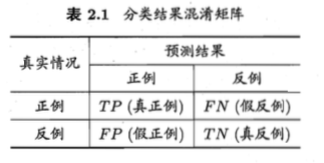
from sklearn.metrics import confusion_matrix pipe_svc.fit(X_train, y_train) y_pred = pipe_svc.predict(X_test) confmat = confusion_matrix(y_true=y_test, y_pred=y_pred) print(confmat) [[71 1] [ 2 40]]
单纯用 错误率,准确率 是无法知道下面的问题,即在正负样本不平衡的情况下,准确率这个评价指标有很大的缺陷。比如在互联网广告里面,点击的数量是很少的,一般只有千分之几,如果用acc,即使全部预测成负类(不点击)acc 也有 99% 以上,没有意义。:
查准率,即精确率,精确率高了,就是误报低:
应用场景 - 当你想知道”挑出的西瓜中有多少比例是好瓜“
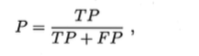
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score, f1_score
print('Precision: %.3f' % precision_score(y_true=y_test, y_pred=y_pred))
Precision: 0.976
查全率,即召回率,召回率高了,就是漏报低:
应用场景 - 当你想知道”所有好瓜中有多少比例被挑出来了“
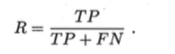
print('Recall: %.3f' % recall_score(y_true=y_test, y_pred=y_pred))
Recall: 0.952
P-R图 (precision - relation):
当一个学习器的P-R曲线被另一个学习器的包住,那么后者性能优于前者。
当有交叉时,需要在具体查准率或者查全率下进行比较。

平衡点(Break Event Point BEP):
即上图中三个红点。
综合考虑查准率,查全率的度量。
当 查准率 = 查全率时的点,谁大谁更优。
F1度量:
也是综合考虑查准率,查全率的度量,比BEP更常用:

print('F1: %.3f' % f1_score(y_true=y_test, y_pred=y_pred))
F1: 0.964
Fβ:
可以表达对查准率,查全率的不同重视程度,
β>1 则查全率有更大影响, β<1 则查准率有更大影响, β=1 则为F1。
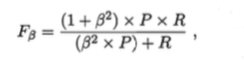
One vs. All (OvA) 分类问题
这时会在 n 个二分类问题上综合考虑查准率,查全率。
宏~ :先在每个混淆矩阵上计算率,再求平均
宏查准率
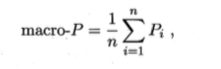
宏查全率
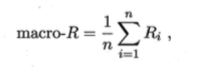
宏 F1
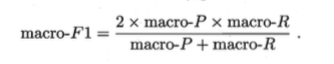
微~ :先将各个混淆矩阵上对应元素求平均,再计算率
微查准率 
微查全率 
微 F1 
ROC:
反映敏感性和特异性连续变量的综合指标,roc曲线上每个点反映着对同一信号刺激的感受性。
纵轴为TPR 真正例率,预测为正并且实际为正的样本占所有正例样本的比例
横轴为FPR 假正例率,预测为正并且实际为负的样本占所有负例样本的比例

对角线对应的是”随机猜想“,
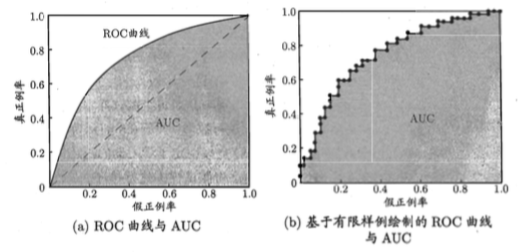
当一个学习器的ROC曲线被另一个学习器的包住,那么后者性能优于前者。
有交叉时,需要用AUC进行比较。
AUC:
ROC曲线下的面积
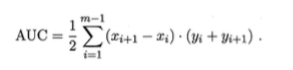
import numpy as np from sklearn.metrics import roc_auc_score y_true = np.array([0, 0, 1, 1]) y_scores = np.array([0.1, 0.4, 0.35, 0.8]) roc_auc_score(y_true, y_scores) 0.75
代价敏感
现实任务中,当不同类型的错误具有不同的影响后果时,他们的代价也是不一样的。
此时,可以设定:
代价矩阵 cost matrix:
如果将第0类预测为第1类的损失更大,则cost01 > cost10,相反将第1类预测为第0类造成的损失更大,则cost01 < cost10:
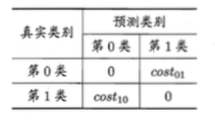
则带有“代价敏感”的错误率为: 
其中 0 为正类,1 为反类,D+ 为正例子集合,D- 为反例子集合。
代价曲线 cost curve:
非均等代价下,反应学习器的期望总体代价。
横轴为取值为[0,1]的正例概率代价: 
纵轴为取值为[0,1]的归一化代价: 
其中 p 为正例的概率,FPR = 1 - TPR。




