validation curve 验证曲线与超参数

验证曲线的作用

我们知道误差由偏差（bias）、方差（variance）和噪声（noise）责成。

偏差：模型对于不同的训练样本集，预测结果的平均误差。

方差：模型对于不同训练样本集的敏感程度

噪声：数据集本身的一项属性

同样的数据（cos函数上的点加上噪声），我们用同样的模型（polynomial），但是超参数却不同（degree=1, 4, 15），会得到不同的拟合效果：

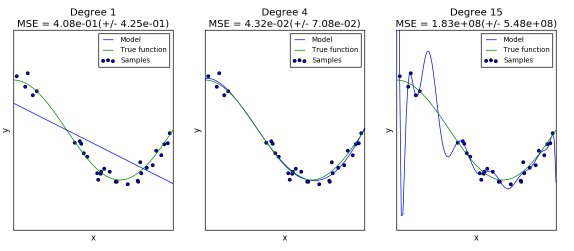
第一个模型太简单，模型本身就拟合不了这些数据（高偏差）；

第二个模型可以看成几乎完美地拟合了数据；

第三个模型完美拟合了所有训练数据，但却不能很好地拟合真实的函数，也就是对于不同的训练数据很敏感（高方差）。

对于这两个问题，我们可以选择模型和超参数来得到效果更好的配置，也就是可以通过验证曲线来调节。

---

验证曲线是什么

验证曲线和学习曲线的区别是，横轴为某个超参数的一系列值，由此来看不同参数设置下模型准确率，而不是不同训练集大小下的准确率。

从验证曲线上可以看到随着超参数设置的改变，模型可能从欠拟合到合适再到过拟合的过程，进而选择一个合适的位置，来提高模型的性能。

需要注意的是如果我们使用验证分数来优化超参数，那么该验证分数是有偏差的，它无法再代表模型的泛化能力，我们就需要使用其他测试集来重新评估模型的泛化能力。

即我们需要把一个数据集分成三部分，train、validation和test，我们使用train训练模型，并通过在validation上的表现不断修改超参数值（例如svm中的C值、gamma值等），当模型超参数在validation上表现最优时，我们再使用全新的测试集test进行测试，以此来衡量模型的泛化能力。

不过有时画出单个超参数与训练分数和验证分数的关系图，有助于观察该模型在相应的超参数取值时，是否过拟合或欠拟合的情况发生。

---

 

适用场景

当拥有大量样本可供使用时，可以将数据分为train、validation和test；当样本数量较少时，可以使用交叉验证，但也一定要留出相同的一部分test数据集，在最后使用。而其余部分假如分成了k-fold，就可以循环让k-1fold做训练集，剩下一个fold做验证集。

---

如何解读

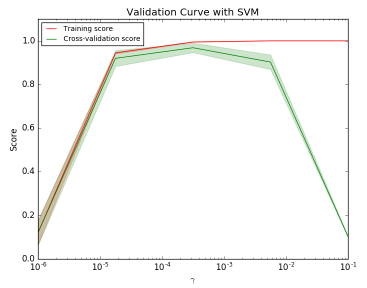
如图是SVM在不同gamma时，它在训练集和交叉验证上的分数：

gamma很小时，训练分数和验证分数都很低，为欠拟合；

gamma逐渐增加时，两个分数都较高，此时模型相对不错；

gamma太高时，训练分数高，验证分数低，学习器会过拟合。

本例中，可以选验证集准确率开始下降，而测试集越来越高那个转折点作为gamma的最优选择。

---

怎么画

下面用SVC为例，调用validation_curve：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_digits

from sklearn.svm import SVC
from sklearn.learning_curve import validation_curve

validation_curve要看的是SVC()的超参数gamma，gamma的范围是取 10^-6 到 10^-1 5 个值， 评分用的是metrics.accuracy_score的accuracy：

param_range = np.logspace(-6, -1, 5)

　　

train_scores, test_scores = validation_curve(
    SVC(), X, y, param_name="gamma", param_range=param_range,
    cv=10, scoring="accuracy", n_jobs=1)

画图时，横轴为param_range，纵轴为train_scores_mean，test_scores_mean：

plt.semilogx(param_range, train_scores_mean, label="Training score", color="r")
plt.semilogx(param_range, test_scores_mean, label="Cross-validation score",
             color="g")