Learning Curve 与 偏差方差 （判断欠过拟合）

 

之前有一篇文章介绍了什么是偏差（bias）与方差（variance），这篇文章介绍一下如何使用学习曲线来判断模型是否处于欠拟合或过拟合。

---

 

什么是学习曲线？

学习曲线就是通过画出不同训练集大小时训练集和验证集的准确率，可以看到模型在新数据上的表现，进而来判断模型是否方差偏高或偏差过高，是否可以通过增加数据集来减少过拟合、是否可以通过增加特征、减少正则项来降低偏差。

---

怎么解读？

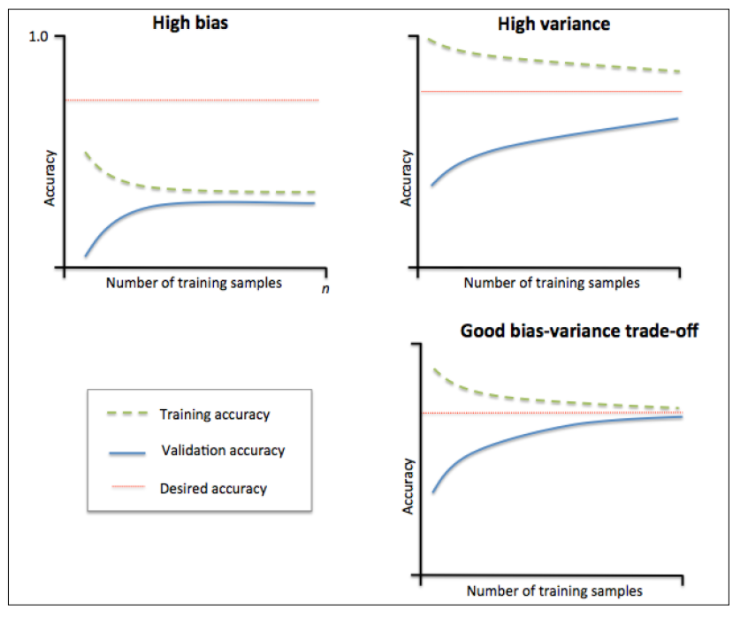
当训练集和测试集的误差收敛但却很高时，为高偏差。

例如左上，偏差很高，训练集和验证集的准确率都很低，很可能是欠拟合。

我们可以增加模型参数，比如，构建更多的特征，减少正则项。

此时通过增加数据量是不起作用的。

 

当训练集和测试集的误差之间有大的差距时，为高方差。

当训练集的准确率比其他独立数据集上的测试结果的准确率要高时，一般都是过拟合。

例如右上，方差很高，训练集和验证集的准确率相差太多，应该是过拟合。

我们可以增大数据集，降低模型复杂度，增大正则项，或者通过特征选择减少特征数。

 

理想情况是找到偏差和方差都很小的情况，即收敛且误差较小。

---

怎么画？

在画学习曲线时，横轴为训练样本的数量，纵轴为准确率。

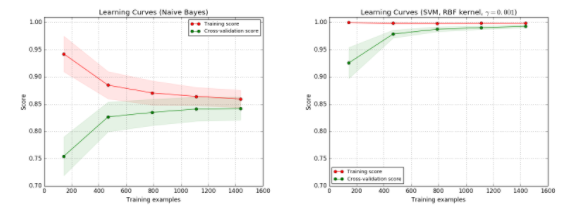
左图为 朴素贝叶斯（Native Bayes）分类器，分数大概收敛在0.85，此时增加数据集对提升结果没有帮助。

右图为 支持向量机（SVM RBF-kernel），训练集的准确率很高，验证集的准确率也随着数据量增加而增加，不过因为训练集还是高于验证集的，处于过拟合状态，所以增加数据集还是对提升结果有帮助的。

---

 

代码实现

模型选择GaussianNB和SVC作比较；

模型选择方法中需要用到learning_curve和交叉验证中的ShuffleSplit

import numpy as np
import matplotlib.pyplot as plt

from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC

from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit

定义画出学习曲线的方法，

核心是调用了sklearn.model_selection的learning_curve，

学习曲线返回的是train_sizes,train_scores,test_scores，

画训练集的曲线时，横轴是train_sizes，纵轴为train_scores_mean，

画测试集的曲线时，横轴是train_sizes，纵轴为test_scores_mean。

def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
                        n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
    ~~~
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
    train_scores_mean = np.mean(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)  
    ~~~     

在调用plot_learning_curve时，首先定义交叉验证cv和学习模型estimator。

这里交叉验证用的是ShuffleSplit，它首先将样例打散，并随机选取20%的数据集作为测试集，这样选出100次，最后返回的是train_index,test_index，就知道哪些数据是训练集，哪些是测试集。

当estimator是GaussianNB，对应左图：

cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)

当estimator是SVC时，对应右图：

cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)