ML中的集成学习

什么是集成学习？

集成学习或者叫元算法，就是对其他算法进行组合的一种方式。毕竟，三个臭皮匠顶个诸葛亮呢。集成学习的处理思路就是这样。

集成学习为什么有效？

不同的模型通常会在测试集上产生不同的误差；如果成员的误差是独立的，集成模型将显著地比其他成员表现更好。

集成学习的基本策略

Boosting方法

• 基于串行策略：基学习器之间存在依赖关系，新的学习器要根据上一个学习器生成。
• 基本思路：
  • 先从初始训练集训练一个基学习器；初始训练集中各样本的权重是相同的；
  • 根据上一个学习器的表现，调整样本权重，使分类错误的样本得到更多的关注；
  • 基于调整后的样本分布，训练下一个基学习器；
  • 测试时，对各基学习器加权得到最终结果
• 特点：
  • 每次学习都会使用全部样本
• 代表算法：
  • AdaBoost
  • GBDT算法

Bagging方法

• 基于并行策略：基学习器之间不存在依赖关系，可同时生成。
• 基本思路：
  • 利用自助采样法对训练集随机采样，重复采样 T 次
  • 基于每个采样集训练一个基学习器，并得到 T 个基学习器；
  • 预测时，集体投票决策

  • 自助采样法：对m个样本的训练集，有放回的采样m次；此时，样本在m次采样中始终没被采样的概率约为0.368，即每次自助采样只能采样到全部样本的63%左右。

  • 
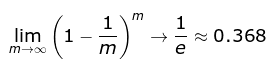
• 特点：
  • 训练每个基学习器时只使用一部分样本；
  • 偏好不稳定的学习器作为基学习器；

  • 所谓不稳定的学习器，指的是对样本分布较为敏感的学习器

Stacking方法

• 基于串行策略：初级学习器与次级学习器之间存在依赖关系，初学习器的输出作为次级学习器的输入。
• 基本思路：
  • 先从初始训练集训练 T 个不同的初级学习器；
  • 利用每个初级学习器的输出构建一个次级数据集，该数据集依然使用初始数据集的标签；
  • 根据新的数据集训练次级学习器；
  • 多级学习器的构建过程类似。

为什么使用决策树作为基学习器？

类似问题

• 基学习器有什么特点？
• 基学习器有什么要求？

使用决策树作为基学习器的原因：

1. 决策树的表达能力和泛化能力，可以通过剪枝快速调整；
2. 决策树可以方便地将样本的权重整合到训练过程中；
3. 决策树是一种不稳定的学习器；  所谓不稳定，指的是数据样本的扰动会对决策树的结果产生较大的影响；

后两点分别适合Boosting策略和Bagging策略；所以它们一般都使用决策树作为基学习器。

为什么不稳定的学习器更适合作为基学习器？

• 不稳定的学习器容易收到样本分布的影响（方差大），很好的引入了随机性；这有助于在集成学习（特别是采用Bagging策略）中提升模型的泛化能力。
• 为了更好的引入随机性，有时会随机选择一个属性子集的最优分裂属性，而不是全局最优（随机森林）。

还有哪些模型也适合作为基学习器？

神经网络

• 神经网络也属于不稳定的学习器；
• 此外，通过调整神经元的数量、网络层数，连接方式初始权重也能很好的引入随机性和改变模型的表达能力和泛化能力。

Bagging方法中能使用线性分类器作为基学习器吗？Boosting呢？

• Bagging方法中不推荐
  • 线性分类器都属于稳定的学习器（方差小），对数据不敏感；
  • 甚至可能因为Bagging的采样，导致训练过程中难以收敛，增大集成分类器的偏差；
• Boosting方法中可以使用
  • Boosting方法主要通过降低偏差的方式来提升模型的性能，而线性分类器本身具有方差小的特点，所以两者有一定的相容性
  • XGBoost中就支持以线性分类器作为基学习器。

Boosting/Bagging与偏差/方差的关系

简单来说，Boosting能提升弱分类器性能的原因是降低了偏差；Bagging则是降低了方差；

• Boosting方法：
  • Boosting的基本思路就是不断减小模型的训练误差（拟合残差或者加大错类的权重），加强模型的学习能力，从而减小偏差；
  • 但Boosting不会显著降低方差，因为其训练过程中各基学习器是强相关的，缺少独立性。
• Bagging方法：
  • 对 n 个独立不相关的模型预测结果取平均，方差是原来的1/n；
  • 假设所有基分类器出错的概率是独立的，超过半数基分类器出错的概率会随着基分类器的数量增加而下降。
• 泛化误差、偏差、方差、过拟合、欠拟合、模型复杂度（模型容量）关系图：