「题解」P7043 「MCOI-03」村国
其实最开始看到这道题目的时候是没有什么做法的,但是看到\(M \le 10 ^ {18}\) 之后感觉应该是个结论题,所以自己画图手玩了一下发现了做法
首先对于一个最开始到达的点,它是好感度最大且编号最小的,并且他只会影响到他周围的点(显然),所以我们先随便画个图:
下文称权值最大且编号最小的点为 \(Max\),与他相连的次大的且编号最小的点为 \(Max_S\)
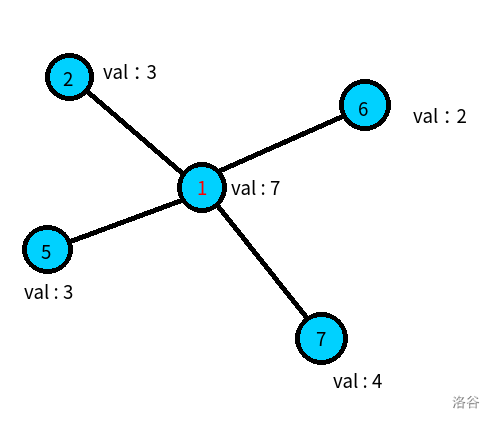
对于这个图,标红的是我们会选择的第一个点,因为他只会对周围的点造成影响,所以不在他周围的次大的点是不会对答案造成贡献的,那么我们会一直选这个点作为 \(Max\) 直到他周围的点和他幸福度相同的时候,如下图
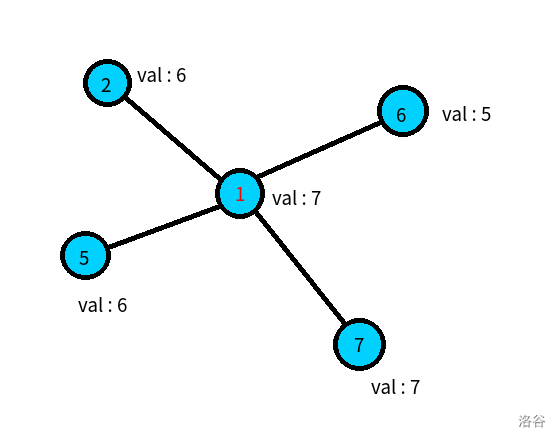
显然,当有一个点的权值和他一样时,我们会选择这两个点中编号较小的一个,在图中是结点1的标号更小,所以我们继续选择一号结点,且这个和第一个 与\(Max\) 权值相同的点一定是 \(Max_S\)那么,当 \(Max_S\) 的优先级 高于 \(Max\) 时,即 \(Max_S\) 成为 \(Max\) 时,原来的 \(Max\) 一定是 \(Max_s\), 这个下文再画图解释

当 \(Max_S\) 成为 \(Max\) 时,即图中的7号结点在第4次更新后,权值变成8,这个时候我们会选择7号结点作为 \(Max\)。接着我们又会更新7号结点周围的点,导致一号结点成为 \(Max\) 然后重复这个操作,那么我们发现,答案最终只会在最初的 \(Max\) 与 \(Max_S\) 中产生。
那么我们先算出 \(Max\) 与 \(Max_S\) 的差值,并且当 \(Max\) 的标号大于 \(Max_S\) 时,交换他们两个的值保证\(Max\) 的标号小于 \(Max_S\),将它与 \(M\) 进行比较,如果 \(M\) 小于这个差值,那么我们直接输出\(Max\) 值,如果大于等于的话,我们将这个差值 % 2,如果余数等于1,输出\(Max_S\),因为这个时候我们选择的是最开始的 \(Max\) 所以更新了 \(Max_S\) 的值使其的幸福度大于 \(Max\) ,而当余数等于0时,我们输出 \(Max\) 因为此时 \(Max\) 与 \(Max_S\) 的幸福度相等,而前者标号小于后者。
记得对 \(n = 1\) 的情况进行特判,因为这个时候我们找不到任何一个 \(Max_S\), 所以直接输出唯一的一个点。
然后对一些上文提到的问题进行解释
当 \(Max_s\) 的优先级 高于 \(Max\) 时,即 \(Max_S\) 成为 \(Max\) 时,原来的 \(Max\) 一定是 \(Max_S\)
\(Q\) : 如果有一个点在 \(Max_S\) 成为 \(Max\) 时与\(Max_S\) 相连且幸福度同样与 \(Max_S\) 相等,标号还要小些怎么办,要选择那个点吗
\(A\) : 你看
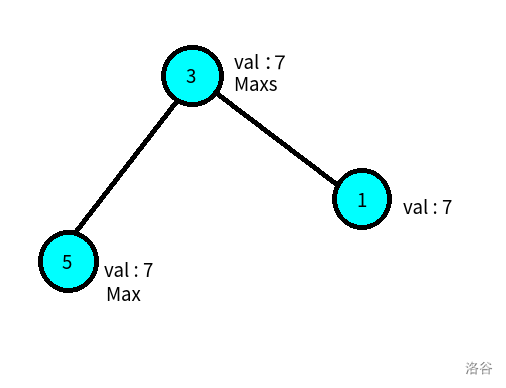
如果存在这样一个点,那么在最开始选择我们这个理想的 \(Max\) 的时候是不会更新这个一号结点的,也就是说一号结点最开始的幸福度就和5号结点一样大,所以在最开始我们就会选择1号结点而不是5号结点,当 \(Max\) 的标号小于 \(Max_S\) 的时候同理。
附上代码
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL MAXN = 2000000 + 10;
LL head[MAXN], to[MAXN << 1], nxt[MAXN << 1];
LL val[MAXN], cnt, Max, Maxs;
inline LL read() {
LL x = 0;char c = getchar();
while (c < '0' || c > '9') c = getchar();
while (c >= '0' && c <= '9') x = x * 10 + c -'0',c = getchar();
return x;
}
int main () {
LL T; T = read();
while(T --) {
memset(head, 0, sizeof(head));
cnt = 0; Max = 0; Maxs = 0;
LL n, m; n = read(); m = read();
for(register LL i = 1; i <= n; i ++) {
val[i] = read();
if(val[Max] < val[i]) Max = i;
}
for(register LL i = 1; i < n; i ++) {
LL x, y; x = read(); y = read();
if(y == Max) swap(x, y);
if(x == Max) {
if(val[Maxs] < val[y]) Maxs = y;
else if(val[Maxs] == val[y])
Maxs = min(Maxs, y);
}
}
if(n == 1) {printf("%lld\n", Max); continue;}
if(val[Max] - val[Maxs] <= m) {
m -= (val[Max] - val[Maxs]);
if(Maxs < Max) swap(Max, Maxs);
if(m % 2 & 1) printf("%lld\n", Maxs);
else printf("%lld\n", Max);
}
else printf("%lld\n", Max);
}
return 0;
}
如果对于文章中有什么疑问或是错误,欢迎在评论或私信提出


