A. 小明修公路

对于每新增的一条边权为 $w$ 的路径 $(u,v)$，我们尝试用其去更新 $d$ 矩阵的值。

具体的，枚举 $x,y$，有：

复杂度 $\mathcal{O}(n^{2}k)$。

B. 小明的字符串

设 $f_{i,j}$ 表示考虑到 $s$ 的前 $i$ 个字符且 $s_i$ 匹配到 $t$ 的第 $j$ 个字符的情况下 $t$ 的出现次数。预处理出 $\mathrm{transfer}(l,c)$ 表示在匹配到 $T$ 的第 $l$ 个字符的情况下在添加一个 $c$ 字符可以匹配到 $T$ 的第几个字符。使用 KMP 预处理即可，进而可以直接转移。

发现其实质上为自动机 DP，内层自动机为 KMP 自动机。

复杂度为 $\mathcal{O}(\left|S\right|\left|T\right|\left|\mathrm{\Sigma }\right|)$。

C. 小明的生日 / [AGC001D] Arrays and Palindrome

我们考虑对被限制相同的字符连边，那么合法的构造即为使得建出的图为联通图。

首先考虑 $m=1$ 时如何处理，发现对于所有 $i\in [0,\lceil \frac{n}{2}\rceil )$，若我们可以使得连通块 $\{i+1,n-i\}$ 与连通块 $\{i+2,n-i-1\}$ 联通，那么我们即可构造出有解方案，进而我们考虑连边 $(1,n-1)$，并依次为回文串边界继续建边 $(2,n-2)$，进而可以得到形如下图的构造，可以发现其一定有解。

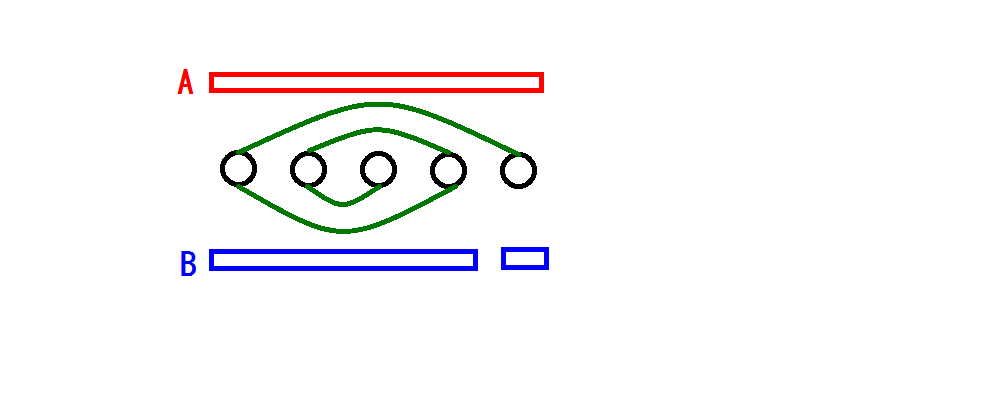
通过上述分析我们可以得到，对于一个长度为 $n$ 的回文串，我们在其端点处添加 $n-1$ 的限制即可使得其元素均相同。下面我们考虑如何扩展到 $m=2$ 的情况，一个直观的想法是我们令 $b$ 序列为 $\{a_1-1,2,a_2-1\}$。发现这样构造其实是通过一个长度为 $2$ 的小回文串使得其相同的。但是这样难于扩展到 $m$ 更大的情况，我们考虑另一种构造。

首先我们取 $b_1=a_1-1$，接下来我们不妨删去字符串的前 $a_i-1$ 个字符，因此我们只需要使得剩余的字符均相同那么即可得到一组合法的构造，那么我们现在的 $a$ 序列实际上为 $\{1,a_2\}$ 发现其与上述 $m=1$ 情况时的 $b$ 序列相似，因此我们取 $b_2=a_2+1$ 即可构造出一组合法方案。

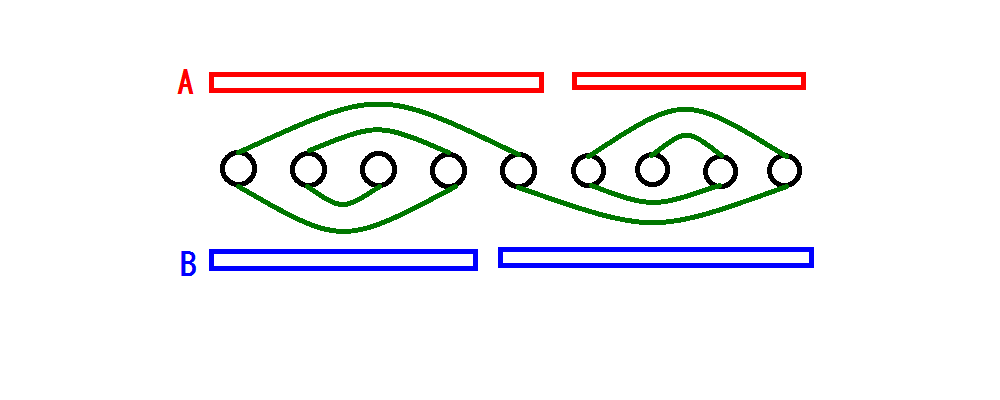
考虑扩展到 $m>2$ 的情况。我们继续使用上述删除前缀的思想，那么问题转化为了 $a=\{1,x\}$ 的情况，另外我们还要求 $\sum b=x$。

我们考虑有解的必要条件，即至少存在 $n-1$ 条边，否则一定无解。

已知 $a$ 数组已经贡献了 $\lfloor \frac{x}{2}\rfloor$ 条边，而可以发现 $b$ 至多贡献 $\lfloor \frac{x}{2}\rfloor$ 条边，因此若 $x$ 为奇数，那么我们至多有 $x-2$ 条边，因此我们在这里只考虑 $x$ 为偶数的情况，后文会证明其他情况一定无解。现在我们已经限制了 $x$ 为偶数，不难发现若 $a=\{1,x\},b=\{x,1\}$ 那么一定合法。因此若 $a$ 中不存在超过两个奇数，我们将这些奇数放到 $a_1$ 或 $a_n$ 的位置上，剩余部分按上述方法处理即可。

进而我们得到了一组合法的构造方式，对于 $iin[2,n-1]$，令 $b_i=a_i$，并且 $b_1=a_1-1,b_2+a_2+1$。

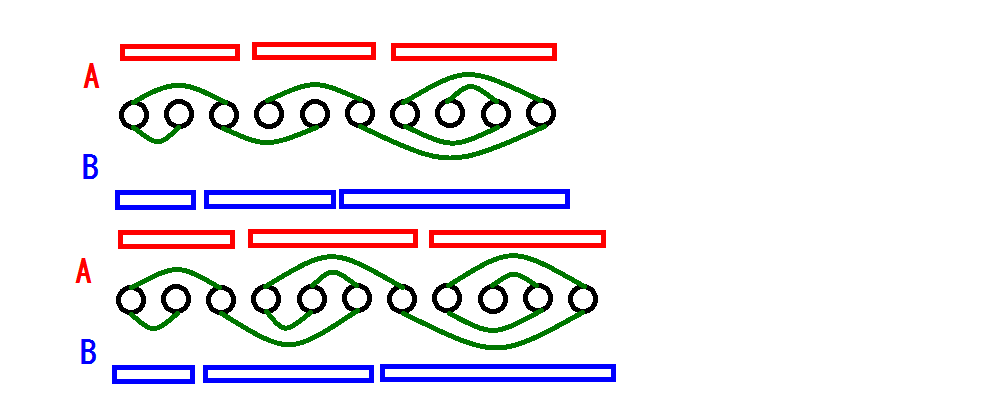
发现我们仅剩下了 $a$ 多与两个奇数的情况未考虑，我们可以发现若 $a$ 中存在多于两个奇数，那么我们一定无法得到 $n-1$ 条边，进而一定无解。

复杂度为 $\mathcal{O}(n)$。

D. 小明的路径

发现若存在度数不小于 $2$ 的节点，那么路径条数关于路径长度是指数级别的，考虑 DP 求解，设 $f_{i,j}$ 以 $i$ 结尾，长度为 $j$ 的路径条数，根据上述分析，该 DP 复杂度为 $\mathcal{O}(n\log V)$。

若不存在度数不小于 $2$ 的节点，那么图中的各个连通块只有孤立点和长度为 $2$ 的链两种。前者的贡献为常数，后者的贡献关于路径条数为一次函数，因此总路径数为关于长度的一次函数，直接求解即可。

复杂度为 $\mathcal{O}(n\log V)$。