Solution Set【2024.1.20】

合集 - Solution Set(35)

29.Solution Set【2024.1.20】2024-01-20

30.Solution Set【2024.1.21】2024-01-21 31.Solution Set【2024.1.27】2024-01-27 32.Solution Set【2024.1.29】2024-01-29 33.Solution Set【2024.2.1】2024-02-01 34.Solution Set【2024.2.15】2024-02-15 35.Solution Set【2024.2.21】2024-02-21

A. 整除

首先特殊考虑 $x = 1$ 的情况，不难发现其合法当且仅当 $\sum c_{i} = m$ 。

对于 $x > 1$ ，我们有

\sum_{i = 0}^{m - 1} x^{i} = \frac{x^{m} - 1}{x - 1}

因此我们不妨考虑 $f (x) = \sum_{i} c_{i} x^{a_{i}} \times (x - 1)$ 在模 $x^{m} - 1$ 意义下的值。

发现在模 $x^{m} - 1$ 意义下，我们有：

x^{m} \equiv x^{0} (\mod x^{m} - 1)

进而我们有：

c x^{a} \equiv c x^{a mod m} (\mod x^{m} - 1)

因此我们可以将 $f (x)$ 转化为一个 $m$ 次多项式，设 $f (x) = \sum_{i = 0}^{m - 1} b_{i} x^{i}$ 。考虑进一步利用上述性质，发现若 $| b_{i} | \geq x$ ，我们可以将其减去 / 加上 $x$ ，同时使得 $b_{(i + 1) mod m}$ 加上 / 减去 $1$ 。不妨称之为「进位」操作，由于 $x > 1$ ，因此这样的操作一定可以减少 $\sum_{i = 0}^{m - 1} | b_{i} |$ 的值，进而减少问题规模。

不难发现通过这样的操作可以使得 $\forall i \in [0, m) \Rightarrow | b_{i} | < x$ ，因此我们只需要考虑在此限制下 $f (x) \equiv 0 (\mod x^{m} - 1)$ 的充要条件即可。首先若 $\forall i \in [0, m) \Rightarrow b_{i} = 0$ ，那么一定有解。

否则我们以 $f (x) > 0$ 的情况为例， $f (x) < 0$ 的情况一定与之对称。首先由于 $\forall i \in [0, m) \Rightarrow | b_{i} | < x$ 不难发现 $max f (x) = \sum_{i = 0}^{m - 1} (x - 1) x^{i}$ ，即当 $\forall i \in [0, m) \Rightarrow b_{i} = x - 1$ 时 $f (x)$ 取到最大值，同时可以发现：

\begin{aligned} max f (x) = & \sum_{i = 0}^{m - 1} (x - 1) x^{i} \\ = & \sum_{i = 1}^{m} x^{i} - \sum_{i = 0}^{m - 1} x^{i} \\ = & x^{m} - 1 \end{aligned}

因此在 $f (x) > 0$ 时，当且仅当 $\forall i \in [0, m) \Rightarrow b_{i} = x - 1$ 时满足 $f (x) \equiv 0 (\mod x^{m} - 1)$ 。

综上，我们可以得出满足 $f (x) \equiv 0 (\mod x^{m} - 1)$ 的三种情况为：

$\forall i \in [0, m) \Rightarrow b_{i} = x - 1$
$\forall i \in [0, m) \Rightarrow b_{i} = 0$
$\forall i \in [0, m) \Rightarrow b_{i} = - (x - 1)$

至此我们得到了一个判定算法：枚举所有的正整数 $x$ ，不断进行上述的「进位」操作，直至满足 $\forall i \in [0, m) \Rightarrow | b_{i} | \leq x$ ，接下来判断是否满足上述三种情况之一，若满足则 $x$ 是一个合法的解。需要注意的是若在进行「进位」操作前满足 $\forall i \in [0, m) \Rightarrow b_{i} = 0$ 那么存在无穷多个解，因此我们需要特殊考虑这种情况。

下面我们尝试分析其复杂度，不难发现对于 $x > {max}_{i = 0}^{m - 1} | b_{i} |$ ，其不会产生任何的「进位」操作，因此对于 $x > {max}_{i = 0}^{m - 1} | b_{i} | + 1$ ，其一定无解（在不考虑无穷多解的情况下）。因此我们需要枚举的 $x$ 上界为 ${max}_{i = 0}^{m - 1} | b_{i} | + 1$ ，由于 $\sum_{i = 0}^{m - 1} | b_{i} |$ 为 $O (n)$ 级别，因此需要枚举的 $x$ 上界为 $O (n)$ 级别。同时发现每次「进位」操作一定会使得 $\sum_{i = 0}^{m - 1} | b_{i} |$ 至少减少 $x - 1$ ，因此最多进行 $O (\frac{n}{x})$ 次「进位」操作。因此在枚举 $x$ 的过程中，我们一共进行了 $O (n \log n)$ 次「进位」操作，考虑使用 std::map 维护 $b_{i}$ 的值，每次「进位」操作的复杂度为 $O (\log n)$ ，完成当前的 $x$ 的所有「进位」操作并判定后恢复 $b_{i}$ 的值即可，总复杂度为 $O (n \log^{2} n)$ 。

Code

#include <bits/stdc++.h>

typedef long long valueType;
typedef std::vector<valueType> ValueVector;
typedef std::vector<ValueVector> ValueMatrix;
typedef std::map<valueType, valueType> ValueMap;
typedef std::set<valueType> ValueSet;
typedef std::map<valueType, ValueSet> SetMap;

void solve() {
    valueType N, M;

    std::cin >> N >> M;

    ValueMap A;
    SetMap bucket;
    valueType count = 0;
    valueType sum = 0;

    for (valueType i = 0; i < N; ++i) {
        valueType c, a;

        std::cin >> c >> a;

        sum += c;

        A[a % M] -= c;
        A[(a + 1) % M] += c;
    }

    if (sum % M == 0)
        ++count;

    {
        auto iter = A.begin();

        while (iter != A.end()) {
            if (iter->second == 0)
                iter = A.erase(iter);
            else
                ++iter;
        }
    }

    if (A.empty()) {
        std::cout << -1 << '\n';

        return;
    }

    for (auto const &[i, a] : A)
        bucket[static_cast<valueType>(a)].insert(static_cast<valueType>(i));

    std::function<bool(valueType)> Check = [&](valueType x) -> bool {
        ValueMap rollBack;

        auto Dec = [&](valueType i, valueType y) {// dec A[i] by y
            bucket[A[i]].erase(i);
            A[i] -= y;
            bucket[A[i]].insert(i);
            rollBack[i] += y;
        };

        auto Inc = [&](valueType i, valueType y) {// inc A[i] by y
            bucket[A[i]].erase(i);
            A[i] += y;
            bucket[A[i]].insert(i);
            rollBack[i] -= y;
        };

        while (bucket.begin()->second.empty())
            bucket.erase(bucket.begin());

        while (bucket.rbegin()->second.empty())
            bucket.erase(std::prev(bucket.end()));

        while (bucket.begin()->first <= -x || bucket.rbegin()->first >= x) {
            while (bucket.begin()->first <= -x) {
                ValueSet const S = bucket.begin()->second;

                for (auto const &i : S) {
                    while (A[i] >= x) {
                        Dec(i, x);

                        Inc((i + 1) % M, 1);
                    }

                    while (A[i] <= -x) {
                        Inc(i, x);

                        Dec((i + 1) % M, 1);
                    }
                }

                while (bucket.begin()->second.empty())
                    bucket.erase(bucket.begin());
            }

            while (bucket.rbegin()->first >= x) {
                ValueSet const S = bucket.rbegin()->second;

                for (auto const &i : S) {
                    while (A[i] >= x) {
                        Dec(i, x);

                        Inc((i + 1) % M, 1);
                    }

                    while (A[i] <= -x) {
                        Inc(i, x);

                        Dec((i + 1) % M, 1);
                    }
                }

                while (bucket.rbegin()->second.empty())
                    bucket.erase(std::prev(bucket.end()));
            }

            while (bucket.begin()->second.empty())
                bucket.erase(bucket.begin());

            while (bucket.rbegin()->second.empty())
                bucket.erase(std::prev(bucket.end()));
        }

        bool const result = bucket.size() == 1 && (bucket.begin()->first == 0 || bucket.begin()->first == x - 1 || bucket.begin()->first == -x + 1);

        for (auto const &[i, y] : rollBack) {
            bucket[A[i]].erase(i);
            A[i] += y;
            bucket[A[i]].insert(i);
        }

        return result;
    };

    valueType max = 0;

    for (auto &[a, c] : A)
        max = std::max(max, std::abs(c) + 1);

    for (valueType i = 2; i <= max; ++i) {
        if (Check(i))
            ++count;
    }

    std::cout << count << '\n';
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

#ifndef LOCAL_STDIO
    freopen("div.in", "r", stdin);
    freopen("div.out", "w", stdout);
#endif

    valueType T;

    std::cin >> T;

    for (valueType testcase = 0; testcase < T; ++testcase)
        solve();

    std::cout << std::flush;

    return 0;
}

B. 词典

考虑对词典建出字典树，发现合法的词典对应的字典树一定满足：

存在 $n$ 个叶子节点，分别对应 $n$ 个单词。
对于父边权值为 $0$ 的节点，其最多有一条权值为 $1$ 的出边。

不难发现满足上述条件的字典树一定是唯一的，对应的词典也一定是合法的。因此我们只需要考虑在满足上述条件的字典树的最小代价即可。

设 $f_{n}$ 表示父边权值为 $1$ 且有 $n$ 个叶子节点的子树的最小代价， $g_{n}$ 表示父边权值为 $0$ 且有 $n$ 个叶子节点的子树的最小代价，那么对于 $n \geq 2$ 我们有：

\begin{aligned} f_{n} = & min_{0 < k < n} {g_{k} + f_{n - k}} + w (n) \\ g_{n} = & f_{n} + w (n) \end{aligned}

其中 $w (n) = \sum_{i = 1}^{n} ⌊ 1 + \log_{2} n ⌋$ ，即代价函数。在计算 $f_{n}$ 时 $k$ 枚举了其权值为 $0$ 的边连向的子树大小， $k \neq 0 \land k \neq n$ 是因为这种情况下一定不会是最优的，因为可以将其拆分为两个子树，从而使得代价更小。将 $g_{n}$ 的定义代入 $f_{n}$ 的式转移式中，我们有：

f_{n} = min_{0 < k < n} {f_{k} + w (k) + f_{n - k}} + w (n)

可以发现 $w (n) - w (n - 1) = ⌊ 1 + \log_{2} n ⌋$ 单调不降，因此 $w (n)$ 下凸，通过归纳可证明 $f_{n}$ 下凸。进而可以推知 $v (k) = f_{k} + w (k) + f_{n - k}$ 同样下凸，求 $f_{n}$ 在凸包上二分即可复杂度为 $O (n \log n)$ 。将 $f_{n - k}$ 视作代价函数可以发现其满足四边形不等式，因此决策点 $k$ 单调不降，复杂度为 $O (n)$ 。需要进一步优化。

不难发现 $w (n)$ 的值为 $O (n \log n)$ ，取 $k = \frac{n}{2}$ 可以得到 $f_{n}$ 的值上界为 $O (n \log^{2} n)$ 。即 $f_{n}$ 差分值的上界为 $O (\log^{2} n)$ ，因此若我们对于每一个差分值 $d$ 求出一个区间 $[l, r]$ 满足 $\forall i \in [l, r] \Rightarrow f_{i} - f_{i - 1} = d$ 。发现对于每个 $d$ ，若我们能得到其区间右端点的值和该位置上的 $f$ 值，那么我们可以通过在该序列上二分得到 $f_{n}$ 的值。考虑如何求出该差分序列。

首先我们可以通过上述算法求出 $[1, n]$ 内 $f_{i}$ 的取值，同时由于决策点 $k$ 单调递增我们可以猜测 $k$ 的最小值是 $n \cdot r$ 级别的，其中 $r$ 是一个 $[0, 1]$ 之间的实数，可以发现当 $n$ 较大时有 $r = \frac{1}{3}$ ，因此实际上我们可以通过 $[1, n]$ 的取值求出 $[1, \frac{n}{1 - r}]$ 内的 $f$ 值。我们可以扩展的这个区间二分出差分值 $d$ 的区间右端点，进而扩展可以求出 $f$ 值的区间，然后继续二分差分值 $d + 1$ 的区间右端点。直至可以求出 $n \leq 10^{15}$ 的 $f_{n}$ 的值。

时间复杂度为 $O (\log^{4} n \log \log n + T \log n)$ 。

Code

#include <bits/stdc++.h>

typedef long long valueType;
typedef std::vector<valueType> ValueVector;

valueType W(valueType n) {// 单次查询复杂度为 O(log n)
    static constexpr valueType const B = 63;

    valueType ans = 0;

    for (valueType i = 0; i < B; ++i) {
        if (n >= (1ll << (i + 1))) {
            ans += (1ll << i) * (i + 1);
        } else {
            ans += (n - (1ll << i) + 1) * (i + 1);
            break;
        }
    }

    return ans;
}

constexpr valueType PreN = 1e5;
ValueVector PreF(PreN + 1);

constexpr double const Rate = 1.3, FindRange = 0.35;// 倍增倍率，查询范围，要求 Rate * (1 - FindRange) <= 1

constexpr valueType MaxDiff = 7000;// 差分数组最大值
constexpr valueType MaxN = 1e15;   // 最大查询范围

std::array<std::pair<valueType, valueType>, MaxDiff> Diff;// 差分数组，first:最大的 m 使得 f_m - f_{m - 1} = i，second: f_m
valueType DiffSize = 0, PreDiff = 0;

void Pre() {// 预处理，复杂度为 O(PreN log PreN)
    ValueVector G(PreN + 1, 0);

    PreF[0] = 0;
    G[0] = 0;
    PreF[1] = W(1);
    G[1] = W(1);

    for (valueType i = 2; i <= PreN; ++i) {
        PreF[i] = std::numeric_limits<valueType>::max();

        valueType l = 1, r = i - 1, point = 1;

        while (l <= r) {
            valueType mid = (l + r) / 2;

            if ((G[mid + 1] - G[mid]) + (PreF[i - (mid + 1)] - PreF[(i - mid)]) >= 0) {
                point = mid;
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        }

        PreF[i] = std::min(PreF[i], G[point] + PreF[i - point]);

        PreF[i] += W(i);

        G[i] = PreF[i] + W(i);
    }

    for (valueType i = 1; i <= PreN; ++i) {
        valueType diff = PreF[i] - PreF[i - 1];

        Diff[diff].first = i;
        Diff[diff].second = PreF[i];

        DiffSize = std::max(DiffSize, diff);
    }

    Diff[DiffSize].first = 0;
    Diff[DiffSize].second = 0;

    --DiffSize;

    PreDiff = DiffSize;
}

valueType F_Extened(valueType n) {
    if (n <= PreN)
        return PreF[n];

    valueType l = PreDiff, r = DiffSize, point = -1;

    while (l <= r) {
        valueType mid = (l + r) / 2;

        if (Diff[mid].first <= n) {
            point = mid;
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }

    if (!(point != -1 && (Diff[point + 1].first >= n || Diff[point].first == n))) {
        std::cerr << "Error: " << n << '\n';
    }
    assert(point != -1 && (Diff[point + 1].first >= n || Diff[point].first == n));

    return Diff[point].second + (n - Diff[point].first) * (point + 1);
}

valueType F_Solve(valueType n) {
    auto Calc = [&](valueType x) -> valueType {
        return W(n) + F_Extened(x) + W(x) + F_Extened(n - x);
    };

    valueType l = n * FindRange, r = n / 2, point = -1;

    while (l <= r) {
        valueType mid = (l + r) / 2;

        if (Calc(mid + 1) >= Calc(mid)) {
            point = mid;
            r = mid - 1;
        } else {
            l = mid + 1;
        }
    }

    // if (!(point != -1 && (Calc(point + 1) >= Calc(point) && Calc(point - 1) >= Calc(point)))) {
    //     throw std::runtime_error("Error");
    // }

    assert(point != -1 && (Calc(point + 1) >= Calc(point) && Calc(point - 1) >= Calc(point)));

    return Calc(point);
}

void MainExtend() {
    Pre();

    valueType max = PreN, nowDiff = PreDiff + 1;

    while (max < MaxN * Rate + 100) {
        valueType const PreMax = max;

        max = max * Rate;

        valueType l = PreMax, r = max, point = PreMax;

        while (l <= r) {
            valueType const mid = (l + r) / 2;

            if (F_Solve(mid) - F_Solve(mid - 1) <= nowDiff) {
                point = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }

        Diff[nowDiff].first = point;
        Diff[nowDiff].second = F_Solve(point);
        max = point;
        ++nowDiff;
        DiffSize = std::max(DiffSize, nowDiff - 1);
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

#ifndef LOCAL_STDIO
    freopen("dictionary.in", "r", stdin);
    freopen("dictionary.out", "w", stdout);
#endif

    MainExtend();

    valueType T;

    std::cin >> T;

    for (valueType testcase = 0; testcase < T; ++testcase) {
        valueType N;

        std::cin >> N;

        std::cout << F_Extened(N) << '\n';
    }

    std::cout << std::flush;

    return 0;
}

C. 蒲公英

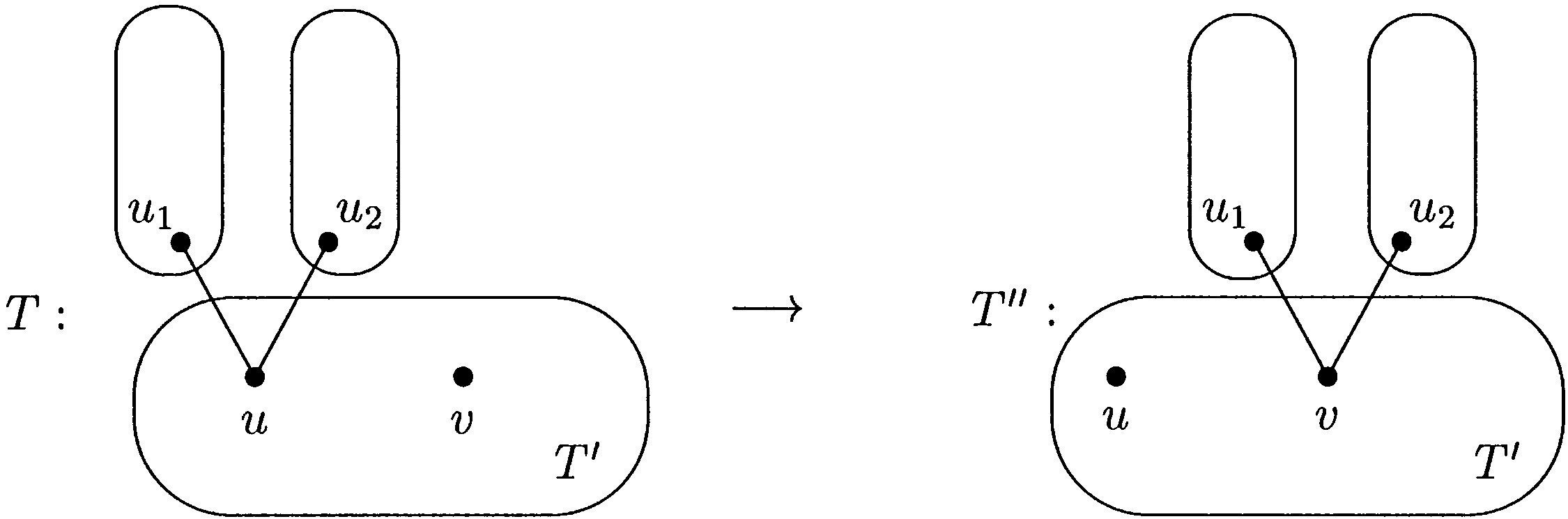
考虑上图的情况， $u_{1}, u_{2}$ 是 $u$ 的两棵子树， $v$ 是 $u$ 在去除 $u_{1}, u_{2}$ 两棵子树后得到树内的任意一点，发现若满足

u_{1} + u_{2} = u + v

那么我们可以将边 $(u_{1}, u)$ 和边 $(u_{2}, u)$ 同时改为 $(u_{1}, v)$ 和 $(u_{2}, v)$ 。发现边 $(u_{1}, v)$ 的权值为：

| v - u_{1} | = | u - u_{2} |

进而可证明更改后的标号方案仍然合法。

发现若 $u$ 存在一棵子树 $u_{0}$ 满足 $2 \cdot u_{0} = u + v$ 那么我们可以将边 $(u_{0}, u)$ 改为 $(u_{0}, v)$ 。得到的标号方案仍然合法。将此类操作表示为 $u \to v$ ，定义 $\frac{u + v}{2}$ 为此操作的中心。

我们考虑找到一个节点 $R$ ，满足任意节点与其的距离不超过 $2$ ，在题目限制下一定存在这样的节点。我们首先构造一个以 $R$ 为根 $n$ 个点的菊花图，然后通过上述两种操作将多余的节点下方给儿子节点即可。

首先可以发现为了满足儿子节点可以完成下放，那么儿子节点的标号一定是 $1, n - 1, 2, n - 3, \dots$ ，且 $R$ 的标号为 $n$ 。发现若 $R$ 的儿子数量为偶数那么存在某个节点无法下放，因此我们考虑删除任意一个儿子节点，之后再将其加入树中，下面我们考虑 $R$ 度数为奇数的情况。

可以发现，为了使得叶子节点可以一直传递下去，我们需要保证任意两次的操作中心尽可能的相近，因此可以发现一种操作方法： $n \to 1, 1 \to n - 1, n - 1 \to 2$ ，不难发现在这种操作方案下操作中心只有两种取值。

因此在执行操作的过程中，除了第一次操作 $n \to 1$ 外，每次均会有一个距离中心最远的节点被留在原地，除此之外，我们还可以通过留下距离中心相等的一对节点。若存在距离中心为 $0$ 的节点且被留下，那么在下一次操作中一定存在一个节点因为没有配对节点而无法继续传递，进而在之后的每次操作中均会有一个节点因为没有配对节点而无法传递。发现若不考虑这种情况那么每次留下的节点个数均为奇数，而在留下距离中心为 $0$ 的节点后，每次留下的节点个数均为偶数。因此我们可以先处理儿子节点个数为奇数的儿子节点，然后再处理儿子节点个数为偶数的儿子节点。不难发现一定可以得出一组合法方案。

下面考虑如何将被删除的子树添加回图中，设经过操作后的菊花图大小为 $m$ ，那么我们现在已经有的节点标号为 ${1, 2, \dots, m}$ ，已经构造出的边的标号为 ${1, 2, \dots, m - 1}$ ，需要添加的边的标号为 ${m, m + 1, \dots, n - 1}$ 。不难发现标号为 $n - 1$ 的边一定只能通过边 $(1, n)$ 得到，因此这条边应在被删除的子树中，那么我们考虑将构造出的菊花图所有节点标号均加 $1$ ，被删除的子树根节点标号为 $1$ ，其子节点从 ${m + 2, m + 3, n}$ 依次标号，可以发现构造出的标号方案一定合法。

复杂度为 $O (n)$ 。

Code

#include <bits/stdc++.h>

typedef long long valueType;
typedef std::vector<valueType> ValueVector;
typedef std::vector<ValueVector> ValueMatrix;
typedef std::deque<valueType> ValueDeque;
typedef std::pair<valueType, valueType> ValuePair;
typedef std::vector<ValuePair> PairVector;
typedef std::deque<ValuePair> PairDeque;

void dfs(valueType x, valueType from, ValueMatrix const &G, ValueVector &depth, valueType &D) {
    if (depth[x] > depth[D])
        D = x;

    for (auto const &iter : G[x]) {
        if (iter == from)
            continue;

        depth[iter] = depth[x] + 1;

        dfs(iter, x, G, depth, D);
    }
}

bool get(valueType x, valueType from, ValueMatrix const &G, valueType goal, ValueVector &path) {
    if (x == goal) {
        path.emplace_back(x);

        return true;
    }

    for (auto const &iter : G[x]) {
        if (iter == from)
            continue;

        if (get(iter, x, G, goal, path)) {
            path.emplace_back(x);

            return true;
        }
    }

    return false;
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

#ifndef LOCAL_STDIO
    freopen("dandelion.in", "r", stdin);
    freopen("dandelion.out", "w", stdout);
#endif

    valueType N;

    std::cin >> N;

    if (N == 1) {
        std::cout << "Yes\n";

        std::cout << 1 << std::endl;

        return 0;
    }

    if (N == 2) {
        std::cout << "Yes\n";

        std::cout << 1 << ' ' << 2 << std::endl;

        return 0;
    }

    ValueMatrix G(N + 1);

    for (valueType i = 1; i < N; ++i) {
        valueType u, v;

        std::cin >> u >> v;

        G[u].emplace_back(v);
        G[v].emplace_back(u);
    }

    valueType Root;

    {
        valueType A = 0, B = 0, L = 0;

        ValueVector depth(N + 1, 0);

        dfs(1, 0, G, depth, A);

        std::fill(depth.begin(), depth.end(), 0);

        dfs(A, 0, G, depth, B);

        L = depth[B] + 1;

        ValueVector path;

        get(A, -1, G, B, path);

        Root = path[L / 2];
    }

    ValueVector ID(N + 1, 0);

    std::sort(G[Root].begin(), G[Root].end(), [&](valueType a, valueType b) {
        if ((G[a].size() & 1) != (G[b].size() & 1))
            return (G[a].size() & 1) < (G[b].size() & 1); // G[x].size() - 1 -> 子树节点数量 (不含自己) (连向根的边代替自己计数)
        else
            return G[a].size() > G[b].size();
    });

    valueType Removed = -1, M = N;

    if ((G[Root].size() & 1) == 0) {
        Removed = G[Root].back();

        G[Root].erase(std::find(G[Root].begin(), G[Root].end(), Removed));
        G[Removed].erase(std::find(G[Removed].begin(), G[Removed].end(), Root));

        M -= G[Removed].size() + 1;
    }

    ID[Root] = M;

    ValueVector next(N + 1);

    {
        valueType x = M;

        for (valueType i = M - 1; i >= 1; --i) {
            if (x > M / 2) {
                next[x] = x - i;

                x = x - i;
            } else {
                next[x] = x + i;

                x = x + i;
            }
        }
    }

    valueType id = M;

    ValueDeque LeftPool, RightPool;

    for (valueType i = (G[Root].size() + 1) / 2 + 1; i <= (M + 1) / 2; ++i)
        LeftPool.emplace_back(i);

    for (valueType i = M - (G[Root].size() + 1) / 2; i > (M + 1) / 2; --i)
        RightPool.emplace_back(i);

    for (auto const &y : G[Root]) {
        id = next[id];

        ID[y] = id;

        valueType const sum = id + next[id];

        auto Dist = [&](valueType x) {
            return std::abs(2 * x - sum);
        };

        G[y].erase(std::find(G[y].begin(), G[y].end(), Root));

        ValueVector set;
        valueType const need = G[y].size();

        set.reserve(need);

        if (need == 0)
            continue;

        if (need == (LeftPool.size() + RightPool.size())) {
            for (auto const &iter : LeftPool)
                set.emplace_back(iter);

            for (auto const &iter : RightPool)
                set.emplace_back(iter);

            LeftPool.clear();
            RightPool.clear();

            for (valueType i = 0; i < need; ++i)
                ID[G[y][i]] = set[i];

            continue;
        }

        while (LeftPool.size() >= 2 && Dist(LeftPool[LeftPool.size() - 1]) == Dist(LeftPool[LeftPool.size() - 2])) {
            RightPool.emplace_back(LeftPool.back());

            LeftPool.pop_back();
        }

        while (RightPool.size() >= 2 && Dist(RightPool[RightPool.size() - 1]) == Dist(RightPool[RightPool.size() - 2])) {
            LeftPool.emplace_back(RightPool.back());

            RightPool.pop_back();
        }

        if (LeftPool.empty() || RightPool.empty() || LeftPool.front() + RightPool.front() != sum) {
            if (LeftPool.empty()) {
                set.emplace_back(RightPool.front());

                RightPool.pop_front();
            } else if (RightPool.empty()) {
                set.emplace_back(LeftPool.front());

                LeftPool.pop_front();
            } else if (Dist(LeftPool.front()) > Dist(RightPool.front())) {
                set.emplace_back(LeftPool.front());

                LeftPool.pop_front();
            } else {
                assert(Dist(LeftPool.front()) < Dist(RightPool.front()));
                set.emplace_back(RightPool.front());

                RightPool.pop_front();
            }
        }

        if ((set.size() & 1) != (need & 1)) {
            assert(Dist(LeftPool.back()) != Dist(RightPool.back()));

            if (Dist(LeftPool.back()) < Dist(RightPool.back())) {
                set.emplace_back(LeftPool.back());

                LeftPool.pop_back();
            } else {
                assert(Dist(LeftPool.back()) > Dist(RightPool.back()));
                set.emplace_back(RightPool.back());

                RightPool.pop_back();
            }
        }

        assert((set.size() & 1) == (need & 1));

        while (set.size() < need) {
            set.emplace_back(LeftPool.front());

            LeftPool.pop_front();

            set.emplace_back(RightPool.front());

            RightPool.pop_front();
        }

        for (valueType i = 0; i < need; ++i)
            ID[G[y][i]] = set[i];
    }

    if (Removed != -1) {
        for (auto &id : ID)
            if (id != 0)
                ++id;

        ID[Removed] = 1;

        valueType count = M + 1;

        for (auto const &y : G[Removed])
            ID[y] = ++count;
    }

    std::cout << "Yes\n";

    for (valueType i = 1; i <= N; ++i)
        std::cout << ID[i] << ' ';

    std::cout << std::endl;

    return 0;
}

[JSOI2011] 分特产

发现若不考虑每个同学都必须至少分得一个特产的限制，那么方案数可以直接计算，考虑到这个限制，我们可以使用二项式反演来计算答案。

设 $f_{k}$ 表示钦定 $k$ 名同学没有分到特产的方案数， $g_{k}$ 表示恰好 $k$ 名同学没有分到特产的方案数，那么我们有：

f_{k} = \sum_{i = k}^{n} (\binom{i}{k}) g_{i}

根据二项式反演，我们有：

g_{k} = \sum_{i = k}^{n} {(- 1)}^{i - k} (\binom{i}{k}) f_{i}

考虑如何计算 $f_{k}$ ，发现此时每种特产独立，因此我们只需要考虑单独每种特产的方案数即可，而单独一种特产的方案就是将 $c_{i}$ 份特产分成 $n - k$ 可以为空的组的方案数，可以使用插板法解决，因此我们有：

f_{k} = \prod_{i} (\binom{c_{i} + n - k - 1}{n - k - 1})

其中 $c_{i}$ 表示第 $i$ 种特产的数量。直接计算 $g_{0}$ 即可，复杂度 $O (n)$ 。

Code

#include <bits/stdc++.h>

typedef long long valueType;
typedef std::vector<valueType> ValueVector;
typedef std::vector<ValueVector> ValueMatrix;

namespace MODINT_WITH_FIXED_MOD {
    constexpr valueType MOD = 1e9 + 7;

    template<typename T1, typename T2>
    void Inc(T1 &a, T2 b) {
        a = a + b;

        if (a >= MOD)
            a -= MOD;
    }

    template<typename T1, typename T2>
    void Dec(T1 &a, T2 b) {
        a = a - b;

        if (a < 0)
            a += MOD;
    }

    template<typename T1, typename T2>
    T1 sum(T1 a, T2 b) {
        return a + b >= MOD ? a + b - MOD : a + b;
    }

    template<typename T1, typename T2>
    T1 sub(T1 a, T2 b) {
        return a - b < 0 ? a - b + MOD : a - b;
    }

    template<typename T1, typename T2>
    T1 mul(T1 a, T2 b) {
        return (long long) a * b % MOD;
    }

    template<typename T1, typename T2>
    void Mul(T1 &a, T2 b) {
        a = (long long) a * b % MOD;
    }

    template<typename T1, typename T2>
    T1 pow(T1 a, T2 b) {
        T1 result = 1;

        while (b > 0) {
            if (b & 1)
                Mul(result, a);

            Mul(a, a);
            b = b >> 1;
        }

        return result;
    }
}// namespace MODINT_WITH_FIXED_MOD

using namespace MODINT_WITH_FIXED_MOD;

class BinomialCoefficient {
private:
    valueType N;
    ValueVector Fact, InvFact;

public:
    BinomialCoefficient() = default;

    BinomialCoefficient(valueType n) : N(n), Fact(N + 1, 1), InvFact(N + 1, 1) {
        for (valueType i = 1; i <= N; ++i)
            Fact[i] = mul(Fact[i - 1], i);

        InvFact[N] = pow(Fact[N], MOD - 2);

        for (valueType i = N - 1; i >= 0; --i)
            InvFact[i] = mul(InvFact[i + 1], i + 1);
    }

    valueType operator()(valueType n, valueType m) {
        if (n < 0 || m < 0 || n < m)
            return 0;

        if (m > N)
            throw std::out_of_range("BinomialCoefficient::operator() : m > N");

        if (n <= N)
            return mul(Fact[n], mul(InvFact[m], InvFact[n - m]));

        valueType result = 1;

        for (valueType i = 0; i < m; ++i)
            Mul(result, n - i);

        Mul(result, InvFact[m]);

        return result;
    }
};

constexpr valueType V = 2005;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    valueType N, M;

    std::cin >> N >> M;

    BinomialCoefficient C(V);

    ValueVector F(N + 1, 1), count(M, 0);

    for (auto &x : count)
        std::cin >> x;

    for (valueType i = 0; i <= N; ++i) {
        for (auto const &x : count)
            Mul(F[i], C(x + (N - i) - 1, (N - i) - 1));
    }

    valueType ans = 0;

    for (valueType i = 0; i <= N; ++i) {
        if (i & 1)
            Dec(ans, mul(F[i], C(N, i)));
        else
            Inc(ans, mul(F[i], C(N, i)));
    }

    std::cout << ans << std::endl;

    return 0;
}

ABC219G Propagation

考虑根号分治，出边集合大小超过 $\sqrt{M}$ 的节点一定不会超过 $\sqrt{M}$ 个。因此我们可以对于每个节点存储与其相邻的，出边集合大小超过 $\sqrt{M}$ 的节点集合，其大小一定不超过 $\sqrt{M}$ 。对于每次操作的节点 $u$ ，我们先通过遍历其存储的节点集合，找出当前其的颜色，然后再根据其出边集合大小进行判断，若其大小小于 $\sqrt{M}$ 则直接暴力进行遍历，否则不处理。

复杂度为 $O ((Q + N) \sqrt{M} + M)$ 。

Code

#include <bits/stdc++.h>

typedef long long valueType;
typedef std::vector<valueType> ValueVector;
typedef std::vector<ValueVector> ValueMatrix;
typedef std::vector<bool> bitset;
typedef std::pair<valueType, valueType> ValuePair;

constexpr valueType B = 600;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    valueType N, M, Q;

    std::cin >> N >> M >> Q;

    ValueMatrix G(N + 1), T(N + 1);
    ValueVector LastTime(N + 1, -1), Color(Q + 1, -1);
    ValueVector Time(N + 1, -1);
    ValueVector A(N + 1);

    std::iota(A.begin(), A.end(), 0);

    for (valueType i = 0; i < M; ++i) {
        valueType u, v;

        std::cin >> u >> v;

        G[u].push_back(v);
        G[v].push_back(u);
    }

    bitset IsLargeDegree(N + 1);

    for (valueType i = 1; i <= N; ++i) {
        if (G[i].size() > B) {
            IsLargeDegree[i] = true;

            for (auto const &to : G[i])
                T[to].push_back(i);
        } else {
            IsLargeDegree[i] = false;
        }
    }

    for (valueType q = 1; q <= Q; ++q) {
        valueType x;

        std::cin >> x;

        valueType last = Time[x];

        for (auto const &from : T[x])
            last = std::max(last, LastTime[from]);

        if (last != Time[x]) {
            A[x] = Color[last];

            Time[x] = last;
        }

        LastTime[x] = q;
        Time[x] = q;
        Color[q] = A[x];

        if (!IsLargeDegree[x]) {
            for (auto const &to : G[x]) {
                A[to] = A[x];

                Time[to] = q;
            }
        }
    }

    for (valueType x = 1; x <= N; ++x) {
        valueType last = Time[x];

        for (auto const &from : T[x])
            last = std::max(last, LastTime[from]);

        if (last != Time[x]) {
            A[x] = Color[last];

            Time[x] = last;
        }
    }

    for (valueType i = 1; i <= N; ++i)
        std::cout << A[i] << ' ';

    std::cout << std::endl;

    return 0;
}

[NOI Online #2 提高组] 游戏

考虑计算钦定 $k$ 回合不平局的方案数，使用二项式反演即可得出恰好 $k$ 回合不平局的方案数。设 $f_{u, i}$ 表示考虑 $u$ 子树内钦定出 $i$ 个具有祖孙关系的点对的方案数，应用树上背包即可计算答案，具体的，依次考虑节点 $u$ 的每个儿子节点 $v$ ，我们有转移：

f_{u, i} = \sum_{i = j + k} f_{u, j} + f_{v, k}

分析其复杂度，发现枚举的 $j, k$ 类似于枚举子树内的所有点，而每次枚举到的点对均在其最近公共祖先处贡献复杂度。因此此动态规划复杂度为 $O (n^{2})$ 。

剩余的部分直接二项式反演即可，不多赘述。

Code

#include <bits/stdc++.h>

typedef long long valueType;
typedef std::vector<valueType> ValueVector;
typedef std::vector<ValueVector> ValueMatrix;

namespace MODINT_WITH_FIXED_MOD {
    constexpr valueType MOD = 998244353;

    template<typename T1, typename T2>
    void Inc(T1 &a, T2 b) {
        a = a + b;

        if (a >= MOD)
            a -= MOD;
    }

    template<typename T1, typename T2>
    void Dec(T1 &a, T2 b) {
        a = a - b;

        if (a < 0)
            a += MOD;
    }

    template<typename T1, typename T2>
    T1 sum(T1 a, T2 b) {
        return a + b >= MOD ? a + b - MOD : a + b;
    }

    template<typename T1, typename T2>
    T1 sub(T1 a, T2 b) {
        return a - b < 0 ? a - b + MOD : a - b;
    }

    template<typename T1, typename T2>
    T1 mul(T1 a, T2 b) {
        return (long long) a * b % MOD;
    }

    template<typename T1, typename T2>
    void Mul(T1 &a, T2 b) {
        a = (long long) a * b % MOD;
    }

    template<typename T1, typename T2>
    T1 pow(T1 a, T2 b) {
        T1 result = 1;

        while (b > 0) {
            if (b & 1)
                Mul(result, a);

            Mul(a, a);
            b = b >> 1;
        }

        return result;
    }
} // namespace MODINT_WITH_FIXED_MOD

using namespace MODINT_WITH_FIXED_MOD;

class BinomialCoefficient {
private:
    valueType N;
    ValueVector _Fact, _InvFact;

public:
    BinomialCoefficient() = default;

    BinomialCoefficient(valueType n) : N(n), _Fact(N + 1, 1), _InvFact(N + 1, 1) {
        for (valueType i = 1; i <= N; ++i)
            _Fact[i] = mul(_Fact[i - 1], i);

        _InvFact[N] = pow(_Fact[N], MOD - 2);

        for (valueType i = N - 1; i >= 0; --i)
            _InvFact[i] = mul(_InvFact[i + 1], i + 1);
    }

    valueType operator()(valueType n, valueType m) {
        if (n < 0 || m < 0 || n < m)
            return 0;

        if (m > N)
            throw std::out_of_range("BinomialCoefficient::operator() : m > N");

        if (n <= N)
            return mul(_Fact[n], mul(_InvFact[m], _InvFact[n - m]));

        valueType result = 1;

        for (valueType i = 0; i < m; ++i)
            Mul(result, n - i);

        Mul(result, _InvFact[m]);

        return result;
    }

    valueType Fact(valueType n) {
        if (n < 0)
            return 0;

        if (n > N)
            throw std::out_of_range("BinomialCoefficient::Fact : n > N");

        return _Fact[n];
    }
};

valueType N;
ValueMatrix G, F;
ValueVector Size, ZeroCount, OneCount;
ValueVector Type;

void dfs(valueType x, valueType from) {
    Size[x] = 1;
    ZeroCount[x] = 0;
    OneCount[x] = 0;

    if (Type[x] == 0)
        ++ZeroCount[x];
    else
        ++OneCount[x];

    F[x][0] = 1;

    for (auto const &to : G[x]) {
        if (to == from)
            continue;

        dfs(to, x);

        ValueVector const PreF = F[x];

        for (valueType i = 0; i <= Size[x] / 2; ++i) {
            for (valueType j = 1; j <= Size[to] / 2; ++j)
                Inc(F[x][i + j], mul(PreF[i], F[to][j]));
        }

        Size[x] += Size[to];
        ZeroCount[x] += ZeroCount[to];
        OneCount[x] += OneCount[to];
    }

    for (valueType i = std::min(Size[x] / 2, (Type[x] == 0 ? OneCount[x] : ZeroCount[x])); i >= 1; --i) {
        if (Type[x] == 0)
            Inc(F[x][i], mul(F[x][i - 1], OneCount[x] - (i - 1)));
        else
            Inc(F[x][i], mul(F[x][i - 1], ZeroCount[x] - (i - 1)));
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    std::cin >> N;

    G.resize(N + 1);
    F.resize(N + 1, ValueVector(N + 1, 0));
    Size.resize(N + 1);
    ZeroCount.resize(N + 1);
    OneCount.resize(N + 1);
    Type.resize(N + 1);

    for (valueType i = 1; i <= N; ++i) {
        char c;

        std::cin >> c;

        Type[i] = c == '0' ? 0 : 1;
    }

    for (valueType i = 1; i < N; ++i) {
        valueType u, v;

        std::cin >> u >> v;

        G[u].push_back(v);
        G[v].push_back(u);
    }

    dfs(1, 0);


    BinomialCoefficient C(N);
    
    for (valueType i = 0; i <= N / 2; ++i)
        Mul(F[1][i], C.Fact(N / 2 - i));

    ValueVector Ans(N + 1, 0);

    for (valueType i = 0; i <= N / 2; ++i) {
        for (valueType j = i; j <= N / 2; ++j) {
            if ((j - i) & 1) {
                Dec(Ans[i], mul(F[1][j], C(j, i)));
            } else {
                Inc(Ans[i], mul(F[1][j], C(j, i)));
            }
        }
    }

    for (valueType i = 0; i <= N / 2; ++i)
        std::cout << Ans[i] << '\n';

    std::cout << std::flush;

    return 0;
}

posted @ 2024-01-20 11:19 User-Unauthorized 阅读(34) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· Solution Set【2024.1.17】

· Solution Set【2024.1.4】

· 2024.6 #征集标题

· noip 前杂题选做

· Last dance

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识？

公告

昵称： User-Unauthorized
园龄： 2年7个月
粉丝： 56
关注： 49

+加关注

2025年3月

日

一

二

三

四

五

六

随笔分类

题解(62)

User-Unauthorized

Solution Set【2024.1.20】

A. 整除

B. 词典

C. 蒲公英

[JSOI2011] 分特产

ABC219G Propagation

[NOI Online #2 提高组] 游戏

公告

搜索

常用链接

我的标签

合集

随笔分类

随笔档案

相册

阅读排行榜

评论排行榜

推荐排行榜

最新评论