决策单调性

DP 计算贡献时，往往需要计算任意两点关于某个函数 $w(i,j)$ 的最大值，如果 $w$ 满足一些性质往往可以降低复杂度。

定义四边形不等式满足对于 $a,b$ 两点 $a<b$，且 $w(a+1,b)+w(a,b+1)\ge w(a,b)+w(a+1,b+1)$。

这个定理可以推广到，对于 $a\le b\le c\le d$ 的四个点，如果 $w(a,d)+w(b,c)\ge w(a,c)+w(b,d)$，同样满足四边形不等式。

考虑我们现在有一个 $n\times m$ 的表，第 $i$ 行第 $j$ 列上的数位 $w(i,j)$，其中 $i\le j$，并且满足四边形不等式，需要你计算每一行的最大值。

考虑分治，设 $f(l,r,L,R)$ 表示我们需要求 $[l,r]$ 行的最优决策点，并且已知这些点都在 $[L,R]$ 列之间。

设 $mid=\lfloor\frac{l+r}{2}\rfloor$，我们暴力计算出第 $mid$ 行的最优决策点 $p$ 列。

考虑四边形不等式 $w(a,d)+w(b,c)\ge w(a,c)+w(b,d)$，令 $A=w(a,d),B=w(b,c),C=w(a,c),D=w(b,d)$，那么 $A+B\ge C+D$。

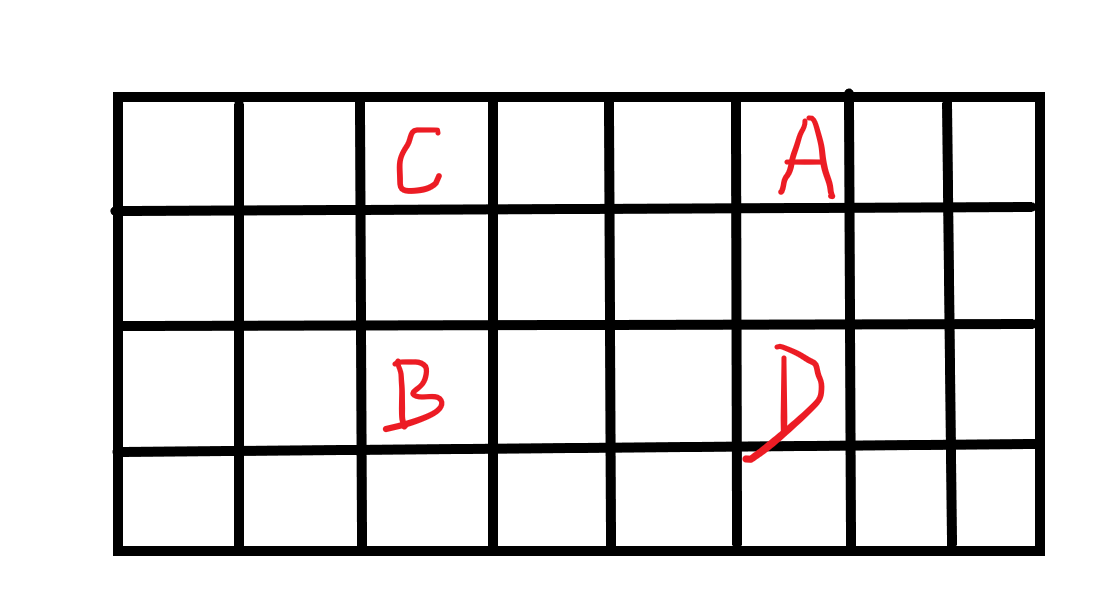
考虑第一种移项方式，$A-C\ge D-B$，那么，如果 $D\ge B$，那么显然有 $A\ge C$，那么如果 $D$ 就是第 $mid$ 行的最优决策点 $p$，那么对于任意列的 $B$ 都满足 $D\ge B$，也就是对于任意的 $C$ 都满足 $C<A$，那么 $[L,p)$ 列永远不可能成为 $[l,mid)$ 行的最优决策点，那么就可以递归到 $f(l,mid-1,p,R)$。

同理，第二种移项方式是 $B-D\ge C-A$，如果 $C\ge A$，那么 $B\ge D$，我们把 $C$ 看作第 $mid$ 行的最优决策点 $p$，那么 $(p,R]$ 列永远不可能成为 $(mid,r]$ 行的最优决策点，递归处理 $f(mid+1,r,L,p)$。