wqs二分学习笔记
怎么总是因为一场模拟赛来填坑啊 /kel
Ubuntu 没有几何画板(悲)
适用问题
题目类型:给定 \(n\) 个物品,要求刚好选择 \(m\) 个,最大/小化权值。
特点:如果没有限制,能够较简单地求出最优解
使用前提:设取 \(k\) 个物品的最优决策是 \(f(k)\) ,那么函数 \(y=f(x)\) 必须具有凹凸性(即凹/凸函数,或者你愿意说图像是个凸包也可以)
算法主体
以下默认讨论的是上凸包。
首先,来考虑对于一个固定的 \(m\) ,如何求出 \(f(m)\) .
对于一个上凸包,有一个显然的性质(定义):随着 \(x\) 轴坐标增大,斜率单调递减。
这样一个具有单调性的东西,容易想到二分。我们可以二分一个斜率 \(k\) ,然后找到斜率为 \(k\) 的直线和这个凸包相切的切点。就像这样:
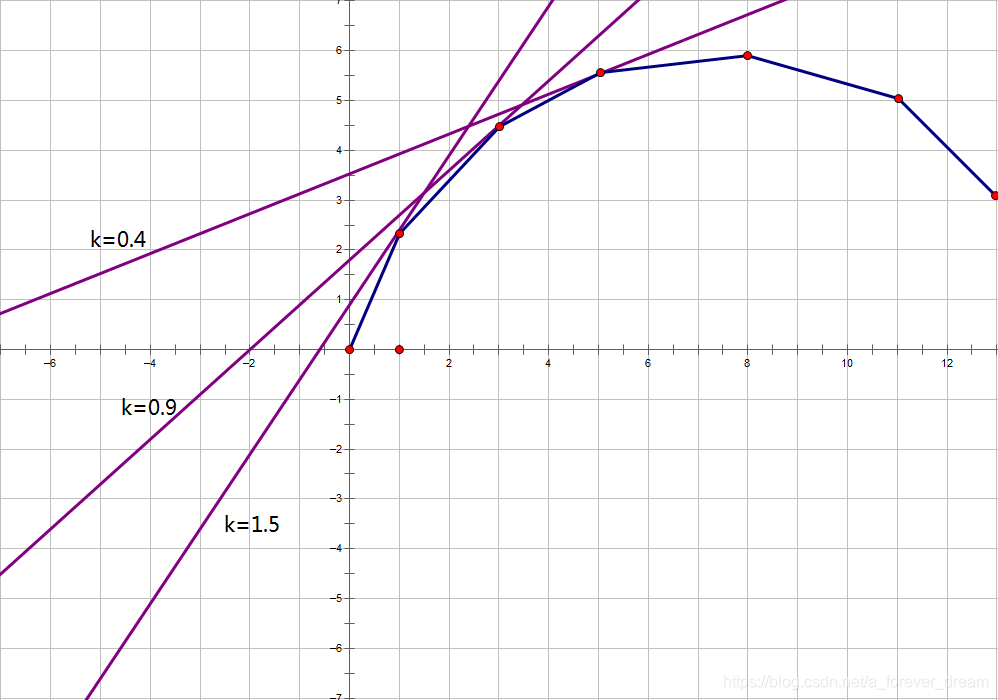
大眼观察得 随着 \(k\) 的减小,切点会向右移动。于是可以二分 \(k\) 直到切点横坐标为 \(m\) ,那么其纵坐标就是答案。
现在的问题就是如何判定切点位置。
考虑多条斜率为 \(k\) 的直线,如下图:
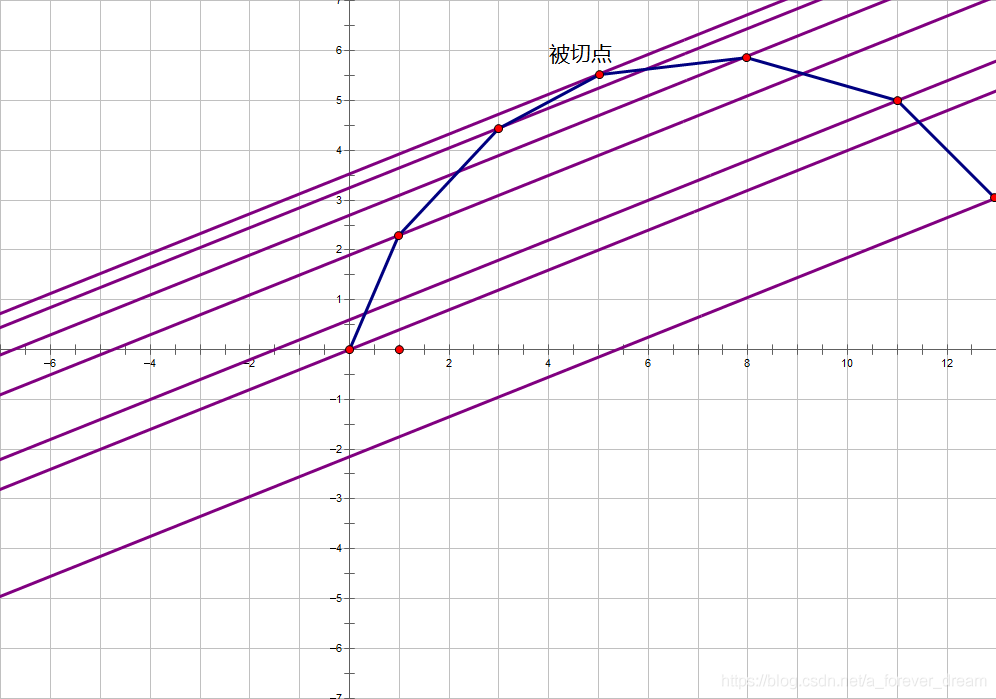
显然,过切点的直线在所有直线中处于最上方,也就是说,直线在 \(y\) 轴上的截距最大。
设截距为 \(b\) ,那么直线方程就是 \(y=kx+b\) . 显然,这等价于给每个物品的权值加上 \(k\) 之后,选了 \(x\) 个物品的总权值。因此,我们可以直接将所有物品的权值加上 \(k\) ,在没有个数限制的情形下计算得到最大的 \(x\) ,然后由于要求的是切点横坐标为 \(m\) 的情况,所以可以根据目前的 \(x\) 对 \(k\) 进行调整,如果 \(x\) 在 \(m\) 左边,那么斜率要减小;反之增大。(当然,这里讨论的是上凸包)
(由于有前提:如果没有限制,能够较简单地求出最优解 ,所以这个 check 是很容易能够在较低的复杂度内实现的)
思路还是很好理解的,结合图像更佳。但是口胡是不行的!我们要做题!代码说明一切
Tree I
给定一个无向带权连通图,每条边是黑/白色,求一棵恰好有 \(need\) 的条白边的最小生成树。
Solution
这道题满足了 “恰好 \(k\) 个” 的限制,且在没有限制的情况下可以轻松地用 Kruskal 求解,因此满足了使用 WQS 二分的前提。
模板题,直接二分然后把所有白边加上这个权值就好了。
有一个细节:如果你跟我一样,写的是整数二分,那么请注意,对于边权相等的情况,需要强制一个 “优先选黑/白边” 的条件,然后根据相应的情况在二分条件中写 >= 或者 <= .
//白边优先的情况
bool operator < ( const Edge &tmp ) const { return (val^tmp.val) ? val<tmp.val : typ<tmp.typ; }
if ( tmp>=k ) l=mid+1,ans=mid;
else r=mid-1;
//黑边优先的情况
bool operator < ( const Edge &tmp ) const { return (val^tmp.val) ? val<tmp.val : typ>tmp.typ; }
if ( tmp<=k ) r=mid-1,ans=mid;
else l=mid+1;
原理的话就是尽可能多选黑/白边,以避免边权相等时出现奇怪的不可控情况,反正只要相等时有个顺序就行了。
//Author: RingweEH
const int N=5e4+10,M=1e5+10;
struct Edge
{
int fro,to,val,typ;
bool operator < ( const Edge &tmp ) const { return (val^tmp.val) ? val<tmp.val : typ<tmp.typ; }
}e[M];
int n,m,k,fa[N];
int find( int x )
{
return (x==fa[x]) ? x : fa[x]=find(fa[x]);
}
int check( int &funcx,int del )
{
for ( int i=1; i<=m; i++ )
if ( e[i].typ==0 ) e[i].val+=del;
sort( e+1,e+1+m );
for ( int i=1; i<=n; i++ )
fa[i]=i;
int tot=0,cnt=0,sum=0;
for ( int i=1; i<=m; i++ )
{
int u=e[i].fro,v=e[i].to; u=find(u),v=find(v);
if ( u==v ) continue;
fa[u]=v; cnt++; tot+=(e[i].typ==0); sum+=e[i].val;
if ( cnt==(n-1) ) break;
}
for ( int i=1; i<=m; i++ )
if ( e[i].typ==0 ) e[i].val-=del;
funcx=sum; return tot;
}
int main()
{
n=read(); m=read(); k=read();
for ( int i=1; i<=m; i++ )
e[i].fro=read()+1,e[i].to=read()+1,e[i].val=read(),e[i].typ=read();
int l=-100,r=100,ans=0; int res=0;
while ( l<=r )
{
int mid=(l+r)>>1,tmp=check( res,mid );
if ( tmp>=k ) l=mid+1,ans=mid;
else r=mid-1;
}
check(res,ans); res=res-ans*k;
printf( "%d\n",res );
return 0;
}
最小度限制生成树
给定一个 \(n\) 点 \(m\) 边带权无向图,求一棵点 \(s\) 正好连了 \(k\) 条边的最小生成树。
Solution
题面中满足了 “正好 \(k\) 个” 的条件,且没有限制的最小生成树很容易求解,前提充分。
显然这里的物品就是和 \(s\) 相连的所有边了。二分 \(k\) 给这些边加上就行。
但是注意数据范围:\(1\leq n \le 5\times 10^4,1\leq m \le 5\times 10^5.\) 如果是 \(\Omicron(m\log ^2 )\) 显然非常的危。
所以可以加一点点 小优化 :
最开始把 \(s\) 连的边和其他边分开,排个序,然后跑最小生成树的时候归并排序即可。
显然这样只需要合并一次,而且所有相连的边增加同一个值,顺序不变。
代码需要注意一些细节和判断无解,如:
- 排序的时候相同权值,和 \(s\) 相连优先
- 如果没有改变权值也不能找出生成树,无解
- 跑出答案之后再找一遍生成树,如果无解或者 \(s\) 的度数不等于 \(k\) 也是无解
- 没给边权范围就离谱,但是我也不知道
int能不能过去
//Author: RingweEH
const int N=5e4+10,M=5e5+10,INF=1e9;
struct Edge
{
int fro,to; ll val;
bool operator < ( const Edge &tmp ) const { return val<tmp.val; }
}e1[M],e2[M],e[M];
int n,m,s,k,tot1=0,tot2=0,fa[N];
ll nowsum;
bool has( Edge x )
{
if ( x.fro==s ) return 1;
if ( x.to==s ) return 1;
return 0;
}
void Merge_Sort()
{
int i=0,j=0,tot=0;
while ( (i<tot1) && (j<tot2) )
{
Edge t1=e1[i+1],t2=e2[j+1];
if ( (t1.val<t2.val) || ((t1.val==t2.val) && (has(t1))) ) e[++tot]=t1,i++;
else e[++tot]=t2,j++;
}
while ( i<tot1 ) e[++tot]=e1[++i];
while ( j<tot2 ) e[++tot]=e2[++j];
}
int find( int x )
{
return (x==fa[x]) ? x : fa[x]=find(fa[x]);
}
int Kruskal()
{
for ( int i=1; i<=n; i++ )
fa[i]=i;
int cnt=0,cnts=0; ll sum=0;
for ( int i=1; i<=m; i++ )
{
int u=e[i].fro,v=e[i].to; ll w=e[i].val;
u=find(u); v=find(v);
if ( u==v ) continue;
fa[u]=v; sum+=w; cnt++;
if ( has(e[i])) cnts++;
if ( cnt==(n-1) ) break;
}
if ( cnt<(n-1) ) return -1;
nowsum=sum; return cnts;
}
int check( int x )
{
for ( int i=1; i<=tot1; i++ )
e1[i].val+=x;
Merge_Sort();
int res=Kruskal();
for ( int i=1; i<=tot1; i++ )
e1[i].val-=x;
return res;
}
int main()
{
n=read(); m=read(); s=read(); k=read();
for ( int i=1; i<=m; i++ )
{
int u=read(),v=read(),w=read();
if ( u==s ) { e1[++tot1].fro=u,e1[tot1].to=v; e1[tot1].val=w; }
else if ( v==s ) { e1[++tot1].fro=v,e1[tot1].to=u; e1[tot1].val=w; }
else { e2[++tot2].fro=u; e2[tot2].to=v; e2[tot2].val=w; }
}
sort( e1+1,e1+1+tot1 ); sort( e2+1,e2+1+tot2 );
if ( check(0)==-1 ) { printf( "Impossible\n" ); return 0; }
int l=-INF,r=INF,ans=-INF;
while ( l<=r )
{
int mid=(l+r)>>1;
if ( check(mid)>=k ) l=mid+1,ans=max(ans,mid);
else r=mid-1;
}
int now=check(ans);
if ( (now==-1) || (now^k) ) printf( "Impossible\n" );
else
{
ll ans_sum=nowsum-ans*k;
printf( "%lld\n",ans_sum );
}
return 0;
}
April Fools' Problem (hard)
\(n\) 道题, 第 \(i\) 天可以花费 \(a_i\) 准备一道题, 花费 \(b_i\) 打印一道题, 每天最多准备一道, 最多打印一道, 准备的题可以留到以后打印, 求最少花费使得准备并打印 \(k\) 道题。\(k,n\leq 5e5\) .
Solution
看到 \(k\) 个东西,就能想到 wqs二分了。
显然,斜率单调不降,因此这题是个下凸包,把每个物品的权值减去 \(mid\) 即可。然后来考虑怎么写 checker .
对于每一天,有三种选择:
- 跳过这一天
- 准备一道题(将可选项中加入一个 \(a_i\) )
- 打印出现过的最小的一个 \(a_i\) (用 \(b_i\) 和之前的 \(a_i\) 配对)
显然这个东西可以用优先队列维护。每个 \(b_i\) 有两种选择:
- 和某个新的 \(a_i\) 配对,取堆顶即可。
- 替换之前某个 \(a_i\) 所配的 \(b_i\) ,这个就直接类似反悔贪心一样搞,往堆里面加入一个 \(b_i-del\) 即可,这样当你访问到 \(b_j\) 的时候,\(b_j-del-val=b_j-del-b_i+del=b_j-b_i\) ,就相当于加入差值了。
那么就做完了。写WQS第一次一遍AC,我不行
奉送双倍经验:[PA2013]Raper
//Author: RingweEH
const int N=5e5+10;
struct Node
{
ll val; int typ;
Node ( ll _val=0,int _typ=0 ) { val=_val; typ=_typ; }
bool operator < ( const Node &tmp ) const { return val<tmp.val; }
};
int n,k;
ll a[N],b[N],sav_sum=0;
priority_queue<Node> q;
int check( ll del )
{
ll sum=0;
for ( int i=1; i<=n; i++ )
{
Node t(-a[i],0); q.push(t);
Node now=q.top();
ll tmp=b[i]-del-now.val;
if ( tmp<0 )
{
sum+=tmp; q.pop();
q.push( Node(b[i]-del,1) );
}
}
int cnt=0; sav_sum=sum;
while ( !q.empty() ) { cnt+=(q.top().typ==1); q.pop(); }
return cnt;
}
int main()
{
n=read(); k=read();
for ( int i=1; i<=n; i++ )
a[i]=read();
for ( int i=1; i<=n; i++ )
b[i]=read();
ll l=0,r=3e9,ans=0;
while ( l<=r )
{
ll mid=(l+r)>>1; int now=check(mid);
if ( now<=k ) l=mid+1,ans=mid;
else r=mid-1;
}
check(ans);
printf( "%lld\n",sav_sum+ans*k );
return 0;
}
忘情
给定一个式子,表示序列的值:
给定一个长度为 \(n\) 的序列,要求分成 \(m\) 段且每段的值之和最小,求最小值。
\(m\leq n\leq 1e5,1\leq x_i\leq 1000\) .
Solution
这式子纯粹是来恶心人的qwq
In fact , 上下除以 \(\bar x\) 就会变成:
这样就清新多了。而且显然平方里面的东西可以前缀和预处理出来。
那么现在就是 DP 一眼题:
但是可惜的是,这是个 \(\Omicron(n^2)\) 的式子……考虑优化。
然后发现,这个式子几乎跟 这道斜优板子 一模一样!(不会斜优请自行前往)
来推个式子:
斜率 \(k=2S[i]\) ,\(x=S[j]\) ,\(b=f[i]-S[i]^2-2S[i]+1\) ,\(y=f[j]+S[j]^2-2S[j]\) .
显然,斜率单增,因此最优决策点单增,可以决策单调性再优化,直接一个单调队列维护就好了。
然后这个 WQS二分 也是个下凸包的板子。
板子套板子.jpg
我有问题 我一开始写成上凸包了 然后又没开 long long (
//Author: RingweEH
const int N=1e5+10;
int n,m,cnt_block[N],q[N];
ll f[N],S[N];
ll X( ll num ) { return S[num]; }
ll Y( ll num ) { return f[num]+S[num]*S[num]-2*S[num]; }
db slope( ll t1,ll t2 ) { return (db)(Y(t2)-Y(t1))/(X(t2)-X(t1)); }
int check( ll del )
{
memset( f,0x3f,sizeof(f) ); memset( cnt_block,0,sizeof(cnt_block) );
int head=1,tail=0; q[++tail]=f[0]=0;
for ( int i=1; i<=n; i++ )
{
while ( head<tail && slope(q[head],q[head+1])<2*S[i] ) head++;
f[i]=f[q[head]]+(S[i]-S[q[head]]+1)*(S[i]-S[q[head]]+1)+del;
cnt_block[i]=cnt_block[q[head]]+1;
while ( head<tail && slope(q[tail-1],q[tail])>slope(q[tail-1],i) ) tail--;
q[++tail]=i;
}
return cnt_block[n];
}
int main()
{
n=read(); m=read();
for ( int i=1; i<=n; i++ )
S[i]=read();
for ( int i=2; i<=n; i++ )
S[i]+=S[i-1];
ll l=0,r=1e16,ans=0;
while ( l<=r )
{
ll mid=(l+r)>>1;
if ( check(mid)<=m ) r=mid-1,ans=f[n]-mid*m;
else l=mid+1;
}
printf( "%lld\n",ans );
return 0;
}
林克卡特树
给定一棵 \(n\) 点带权树,去掉其中 \(k\) 条边,再加上 \(k\) 条边权为 \(0\) 的边。可以任意选择两点 \(p,q\) ,求 \(p,q\) 树上路径的边权和的最大值。求这个值。
\(1\leq n\leq 3e5,0\leq k\leq 3e5,k<n,|v_i|\leq 1e6\)
Solution
将一棵树删去 \(k\) 条边,会出现 \(k+1\) 个连通块,而新的边边权为 \(0\) ,对答案没有贡献,也就是说,我们只需要求出每个连通块内的直径即可。
放回原树上,其实我们并不用真的删去 \(k\) 条边,而是转化成选择了 \(k+1\) 条不相邻的链/点(也就是删完之后每个连通块的直径)。
这个问题显然可以用 DP 解决。设 \(f[u][i]\) 表示子树 \(u\) 中选择了 \(i\) 条链的最大价值。
然而这样好像并不利于转移 考虑一些特殊性质。
注意到最后的链是不相交的,因此每个点的度数至多为 \(2\) . 不妨再增设一维状态:\(f[0/1/2][u][i]\) 表示点 \(u\) 的度数。设当前子树为 \(v\) ,考虑三种情况:
- \(u\) 度数为 \(0\) . \(f[0][u][i]=\max(f[0][u][j]+\max(f[0/1/2][v][i-j]))\)
- \(u\) 度数为 \(1\),说明点 \(u\) 处是一条链的端点,\(f[1][u][i]=\max(f[1][u][j]+f[0][v][i-j],f[0][u][j]+f[1][v][i-j]+w(u,v))\)
- \(u\) 度数为 \(2\) ,说明点 \(u\) 处被一条链经过,\(f[2][u][i]=\max(f[2][u][j]+f[0][v][i-j],f[1][u][j]+f[1][v][i-j+1]+w(u,v))\)
这样就完成了 DP 部分。显然,这样的时间复杂度是 \(\Omicron(nk)\) ,因为还要枚举一个 \(j\) .
那么现在就可以往上套 WQS二分 了。此时的函数值 \(f(x)=\max(f[0/1/2][rt][x])\) .
注意到,每增加一条链,有两种方式:
- 再找一条链
- 拆开一条链
显然,每一次操作都是选择当前的最优解,新的操作不优于上一个,因此函数图像是上凸包。
那么在 DP 外套上一个 WQS二分,去掉关于每个点选了几条链的次数限制,时间复杂度 \(\Omicron(n)\) ,总时间复杂度 \(\Omicron(n\log k)\) ,可以通过本题。
洛谷 O2 第一页了w 然而 LOJ 上已经排不上号了
实现的时候有一些细节:
- 合并两条链的时候要补上多减了一次的代价
- 最后要对“只选一个点”的情况取 \(\max\) .
- DFS 开头注意清空,对于 \(f[0][u]\) 的情况是 \(0\) ,但是另外两个是负权。
- 记录选的链数挺麻烦的,建议直接写结构体重载
//Author: RingweEH
const int N=3e5+10,INF=1e9;
struct Edge
{
int to,nxt; ll val;
}e[N<<1];
struct Node
{
ll x; int cnt;
Node ( ll _x=0,int _cnt=0 ) : x(_x),cnt(_cnt) {}
Node operator + ( const Node &tmp ) const { return Node(x+tmp.x,cnt+tmp.cnt); }
bool operator < ( const Node &tmp ) const { return ( x<tmp.x || (x==tmp.x && cnt<tmp.cnt) ); }
void clear() { x=-INF; cnt=-INF; }
}f[N][3];
int n,k,tot=0,head[N];
void add( int u,int v,ll w )
{
e[++tot].to=v; e[tot].nxt=head[u]; head[u]=tot; e[tot].val=w;
}
void dfs( int u,int fa,ll del )
{
f[u][0]=Node(0,0); f[u][1].clear(); f[u][2].clear();
for ( int i=head[u]; i; i=e[i].nxt )
{
int v=e[i].to;
if ( v==fa ) continue;
dfs( v,u,del );
f[u][2]=max( f[u][2]+f[v][0],f[u][1]+f[v][1]+Node(e[i].val+del,-1) );
f[u][1]=max( f[u][0]+f[v][1]+Node(e[i].val,0),f[u][1]+f[v][0] );
f[u][0]=f[u][0]+f[v][0];
}
f[u][1]=max( f[u][1],f[u][0]+Node(-del,1) );
f[u][0]=max( f[u][0],max(f[u][1],f[u][2]) );
}
int main()
{
n=read(); k=read(); k++;
for ( int i=1; i<n; i++ )
{
int u=read(),v=read(); ll w=read();
add( u,v,w ); add( v,u,w );
}
ll l=-INF,r=INF,ans=0;
while ( l<=r )
{
ll mid=(l+r)>>1; dfs( 1,0,mid );
if ( f[1][0].cnt>=k ) l=mid+1,ans=f[1][0].x+k*mid;
else r=mid-1;
}
printf( "%lld\n",ans );
return 0;
}
What's More
事实上,WQS二分是可以优化费用流的!没想到吧
考虑这样一个经典问题:
给定一个长度为 \(n\) 的序列 \(a\) ,要求超出恰好 \(k\) 个不相交的连续子序列,使得和最大。
复杂度要求:\(\Omicron(n\log n)\) ,\(n,k\) 同级。
事实上,这是个费用流模型。
对于序列中每个点,拆分成两个点 \(i,i'\) ,连一条 \(i\to i'\) ,流量为 1,费用 \(a_i\) 的边。
对于每个 \(i\) ,连 \(S\to i\) ,流量为 1,费用为 0 .
对于每个 \(i'\) ,连 \(i'\to T\) ,流量为 1,费用为 0 .
对于相邻点 \(i,i+1\) ,连 \(i'\to i+1\) ,流量为 1,费用为 0.
显然这样每次沿着最大费用路径单路增广一次,就相当于选择了原问题的一个最大连续子序列。
增广 \(k\) 次就是答案,由于有反向边,所以不会出现区间相交的情况。
然后就有两种方法:
第一,数据结构优化。
把模型放到原问题上,每次增广就是求全局的最大连续子序列和,然后取反。
那么可以用线段树维护这个操作,复杂度 \(\Omicron(k\log n)\) .
第二,考虑特殊性质。
由于每次单路增广的是最长路,那么增广之后的网络显然是残余网络,每次得到的费用会比上一次少。
也就是说,增广 \(x\) 次后的流量 \(f(x)\) 是个上凸包。
事实上 \(f(x)\) 就是选了 \(x\) 个不相交的连续子序列的最大和。
那么到这里就和上面的WQS二分重合了。
后记
其实难度主要是想到用这个东西,和 checker 里面的东西吧,正经 WQS二分并不难写。
WQS学习文章/图源:wqs二分详解
费用流部分来源于: wqs二分/dp凸优化
大部分题目来源:wqs二分学习笔记


 浙公网安备 33010602011771号
浙公网安备 33010602011771号