FFT & NTT 学习笔记

机房人均多项式带师，就我啥都不会！

所以来填坑了qwq

FFT

前置知识

复数：$z=a+bi$ ，其中 $i=\sqrt{-1}$ . 复数可以表示在复平面上，$z$ 横坐标为 $a$ ，纵坐标为 $b$ . 简单了解复数 “幅角”、“模长”的概念。

基础三角比。知道 $\sin,\cos,\tan$ .

卷积概念：形如 $C[k]=\sum_{i\oplus j=k}A[i]B[j]$ 的式子成为卷积，其中 $\oplus$ 为运算符。多项式乘法就是加法卷积。

DFT & IDFT 思想

$F(x)=a_nx^n+a_{n-1}x^{n-1}+\dots +a_0$ 是多项式的 系数表示法 。手模一下就会知道，这样算卷积（ $F(x)*P(x)$ ）是 $\mathcal{O}(n^2)$ 的。

注意到 $n+1$ 个点及其对应的 $F(x)$ 可以唯一确定一个 $n$ 次多项式，所以又有了 点值表示法 ，即用 $n+1$ 个有序数对来表示一个多项式。

设 $F(x)$ 可以表示为数列 $X=\{x_0,x_1,\dots,x_n\}$ ，$G(x)$ 表示为 $Y=\{y_0,y_1,\dots y_n\}$ （这里省略了点的横坐标，默认两个数列对应同一组横坐标），那么不难想到， $F(x)*G(x)$ 可以表示为 $\{x_0y_0,x_1y_1,\dots ,x_ny_n\}$ ，毕竟卷积就是两个多项式相乘，将某个具体值 $x$ 带入的结果显然和将 $x$ 分别带入再相乘是一样的。但是这里其实有个小问题，就是 $(F*G)(x)$ 的次数是 $2n$ 的，所以事实上需要 $2n+1$ 个点值才能得到确定的结果。这样做一次卷积是 $\mathcal{O}(n)$ 的。

然而我们需要的是系数系数表示法。所以不难想到实现卷积的流程：系数转点值（求值） $\to $ 点值相乘 $\to$ 点值转系数（插值）。

在 FFT 中，第一步叫做 DFT ，最后一步叫做 IDFT （ DFT 逆运算）。

单位根

前面已经提到了有复平面这个东西。现在我们在上面以原点为圆心，画一个半径为 $1$ 的单位圆，并对它进行 $n$ 等分：

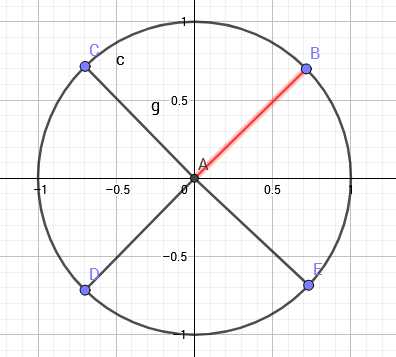如图，这是 $8$ 等分的结果。

现在 单位根 出现了：以原点为起点，上面得到的 $n$ 等分点为终点，作 $n$ 个向量，设幅角为正且最小的向量对应的复数为 $\omega_n$ ，称为 $n$ 次单位根。根据复数乘法不难得到，其余 $n-1$ 个向量对应复数依次为 $\omega_n^2,\omega_n^3,\dots ,\omega_n^n$ . 特别地，$\omega_n^0=\omega_n^n=1$ .（即 $x$ 轴正方向的那个向量）比如上图中，$\vec{AB}$ 就代表了 $\omega_8$ .

这里有一些相关性质：

$\omega_n^k=(\omega_n^1)^k$ ，乘一个 $\omega_n^1$ 的几何意义就是把幅角逆时针转动 $\dfrac{1}{n}$ 个周角。
$\omega_n^j\times \omega_n^k=\omega^{j+k},\omega_{2n}^{2k}=\omega_n^k$
如果 $n$ 为偶数，那么有 $\omega_n^{k+n/2}=-\omega_n^k$ ，相当于转了半个周角，自然是取反。

FFT

现在来考虑一个 $n-1$ 次多项式 $F(x)$ ，每一项按照下标奇偶分开：（这里设 $n$ 是 $2$ 的幂次，不是可以在高次补一些系数为 $0$ 的项）

\[F(x)=(a_0+a_2x^2+\dots +a_{n-2}x^{n-2})+(a_1x+\dots +a_{n-1}x^{n-1}) \]

为了方便，记

\[FL(x)=a_0+a_2x^2+\dots+a_{n-2}x^{n/2-1},FR(x)=a_1+a_3x+\dots+a_{n-1}x^{n/2-1} \]

那么有

\[F(x)=FL(x^2)+xFR(x^2) \]

现在把 $\omega_n^k$ 代入：

$k<n/2$ ，代入 $\omega_n^k$

\[F(\omega_n^k)=FL\left((\omega_n^k)^2\right)+\omega_n^kFR\left((\omega_n^k)^2\right)=FL(\omega_{n/2}^k)+\omega_n^kFR(\omega_{n/2}^k) \]

$k<n/2$ ，代入 $\omega_n^{k+n/2}$

\[\begin{aligned} F\left(\omega_n^{k+n/2}\right) &=FL\left(\omega_n^{2k+n}\right)+\omega_n^{k+n/2}FR\left(\omega_n^{2k+n}\right)\\\\ &=FL\left(\omega_n^{2k}\right)-\omega_n^{k}FR\left(\omega_n^{2k}\right)\\\\ &=FL\left(\omega_{n/2}^k\right)-\omega_n^{k}FR\left(\omega_{n/2}^k\right)\\\\ \end{aligned} \]

于是这两个式子只有 $FR$ 前面的符号不同。所以如果 $FL(x),FR(x)$ 在 $\omega_{n/2}^0,\cdots,\omega_{n/2}^{n/2-1}$ 的点值表示，就能 $\mathcal{O}(n)$ 求出 $F(x)$ 在 $\omega_n^0,\cdots ,\omega_n^{n-1}$ 的点值表示。显然，这样的过程可以直接分治实现。

上面已经实现了 DFT ，现在来看 IDFT ，即 DFT 的逆运算。

有结论：把 DFT 中的 $\omega_n^1$ 换成 $\omega_n{-1}$ ，用卷积之后得到的多项式放进去做一遍，然后除以 $n$ 即可。具体证明参见文末参考文献。

于是这样 DFT 和 IDFT 就能一个函数实现了。

具体实现

预处理单位根 & 合并

如果正常每次算一遍单位根，复杂度是 $\mathcal{O}(n\log n)$ 的，预处理出单位根就是 $\mathcal{O}(n)$ ，能减小很多常数。

首先用 $\left(\cos\left(\dfrac{2\pi}{n}\right),\sin\left(\dfrac{2\pi}{n}\right)\right)$ 求出 $\omega_n^1$ ，其余直接复数乘上去即可。复数手写结构体就好，当然不怕常数也能用 STL 。

一种更优的写法看代码实现。

合并数组时，最简单的方法就是开一个临时数组，用当前 $f$ 往那里贡献，最后再 copy 一遍。这样显然不优良。

尝试改变赋值顺序，类似 DP 一样分析 $f$ 贡献时哪些会改变，只要保证当前往结果贡献的这部分还是这一轮之前（也就是没被这一轮操作覆盖）的结果就可以了。

蝴蝶变换

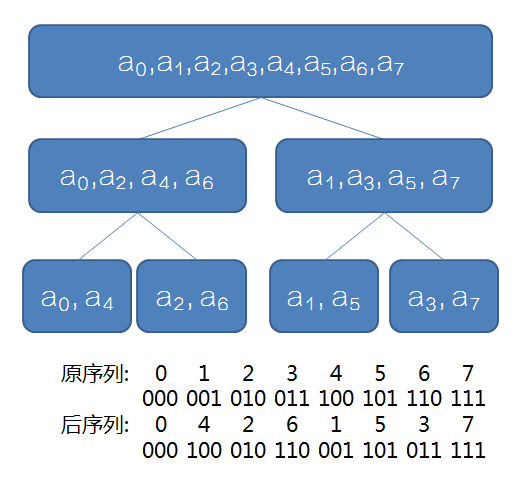
观察我们奇偶分治的过程，发现最后的序列下标对应原序列下标二进制翻转之后的结果。那么我们并不需要每次都把一个数组拷来拷去，还按照奇偶分成两个，可以预处理出二进制翻转的结果，直接赋值。这样通过递推实现，复杂度是 $\mathcal{O}(n)$ 的。

for ( int i=0; i<lim; i++ )
	rev[i]=(rev[i>>1]>>1) | ((i&1) ? lim>>1 : 0);

注意后面的 rev[i>>1]>>1 ，记住当前是以 $lim-1$ （某个二进制下全 $1$ 的东西）为最高位的， rev[i>>1] 的末尾会多出来一位，要把这一位去掉。比如 rev[1]=100 ，而 rev[2]=(100>>1)|0 ，010 先右移取了前两位，但是这是 实际的值 ，正常的没有翻转的 $1$ 是会在最开头再多一个 $0$ 的，所以翻转之后要把这个 $0$ 扔掉。~~不懂就手模~~

三次变两次

令 $P(x)=F(x)+G(x)i$ ，那么 $P(x)^2=F(x)^2-G(x)^2+2F(x)G(x)i$ ，所求就是虚部的一半。所以只需要两次 FFT 即可。

Warning：值域相差过大会卡精度，可以数乘到相同值域再做。

模板

题目链接这题输入输出量比较大，所以快读快写能起到很大的优化。这个板子大概是平均 930ms 左右。

//Author:RingweEH
//P3803 【模板】多项式乘法（FFT）
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
char buf[1<<20],*p1=buf,*p2=buf;
int read()
{
	int x=0; char ch=getchar();
	while ( ch>'9' || ch<'0' ) ch=getchar();
	while ( ch<='9' && ch>='0' ) x=x*10+ch-48,ch=getchar();
	return x;
}
void write( int x ) { if(x<0) putchar(45); if ( x>9 ) write(x/10); putchar(x%10+48); }
const int N=2100000;
const db PI=acos(-1.0)*2;
int n,m,rev[N];
struct Complex
{
	db x,y;
	Complex( db _x=0,db _y=0 ) : x(_x),y(_y) {}
}F[N];//,G[N];
Complex operator + ( Complex t1,Complex t2 ) { return Complex(t1.x+t2.x,t1.y+t2.y); }
Complex operator - ( Complex t1,Complex t2 ) { return Complex(t1.x-t2.x,t1.y-t2.y); }
Complex operator * ( Complex t1,Complex t2 ) { return Complex(t1.x*t2.x-t1.y*t2.y,t1.x*t2.y+t1.y*t2.x); }

void FFT( Complex *f,bool fl )
{
	int i,k,len,l;
	for ( i=0; i<n; i++ ) 		//交换到最终位置
		if ( i<rev[i] ) swap( f[i],f[rev[i]] );
	for ( k=2,len; k<=n; k<<=1 )		//枚举步长，也就是每次合并的两个区间长度总和
	{
		len=k>>1; Complex w(cos(PI/k),sin(PI/k));		//w是单位根
		if ( !fl ) w.y*=-1;
		for ( i=0; i<n; i+=k )		//枚举每个大区间
		{
			Complex buf(1,0);
			for ( l=i; l<i+len; l++ )	
			{
				Complex tmp=buf*f[len+l];
				f[len+l]=f[l]-tmp; f[l]=f[l]+tmp;
				buf=buf*w;
			}
		}
	}
}

int main()
{
	n=read(); m=read(); int i;
	for ( i=0; i<=n; i++ ) F[i].x=read();
	for ( i=0; i<=m; i++ ) F[i].y=read();
	
	for ( m+=n,n=1; n<=m; n<<=1 );
	for ( i=0; i<n; i++ ) rev[i]=(rev[i>>1]>>1)|((i&1) ? n>>1 : 0);
	FFT( F,1 ); //FFT( G,1 );		//DFT
	for ( i=0; i<n; i++ ) F[i]=F[i]*F[i];
	FFT( F,0 );						//IDFT
	for ( i=0; i<=m; i++ )
		write((int)(F[i].y/n/2+0.49)),putchar(32);
		//printf( "%d ",(int)(F[i].y/n/2+0.49) ); //printf( "%d ",(int)(F[i].x/n+0.49) );

	return 0;
}

NTT

前置知识

如果 $a,p$ 互质且 $p>1$ ，对于 $a^n\equiv 1(\bmod p)$ 最小的 $n$ ，称为 $a$ 模 $p$ 的阶，记为 $\delta_p(a)$ .

原根

FFT 依赖单位根，所以必须采用浮点数，引发精度问题。NTT 就是 FFT 在模意义下的替代品。这里，原根代替了单位根。

先考虑单位根有哪些性质：

$\omega_n^k=(\omega_n^1)^k$
$\omega_n^{0\sim n-1}$ 互不相同
$\omega_n^k=\omega_n^{k\bmod n}$ 。前三条等价于 $\omega_n^1$ 在模意义下阶恰为 $n$ .
$\omega_{2n}^{2k}=\omega_n^k$

原根的定义：对于一个素数 $p$ ，如果 $g$ 的阶达到 $p-1$ 的上界，称 $g$ 为原根。

注意到 $g^k$ 的阶恰为 $(p-1)/\gcd(k,p-1)$ ，这个数仍然是 $p-1$ 的约数。所以，当 $n\nmid (p-1)$ 时，找不到阶恰为 $n$ 的数。

当 $n\mid (p-1)$ 时，$g^{(p-1)/n}$ 的阶为 $n$ ，且不难发现也满足最后一个条件。

由于算法中 $n$ 往往是 $2$ 的幂次，我们只需要构造一个质数 $p$ 使得 $p-1$ 包含大量因子 $2$ 即可。

常用原根：详细版本不用原根的 trick

$p$	$g$
$998244353=119\cdot 2^{23}+1$	$3$
$2281701377=17\cdot 2^{27}+1$	$3$
$1004535809=479\cdot 2^{21}+1$	$3$

具体实现

为什么没有算法讲解？因为没有本质区别QWQ

额外技巧：

预处理原根
由于只有加减法操作，可以用 unsigned long long 存储，能承受大概 18*Mod*Mod 的范围，所以常规范围下可以不取模，范围较大就中间取模，尽量减少次数。

附送正常版的 NTT：

//Author:RingweEH
//P3803 【模板】多项式乘法（FFT）
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
char buf[1<<20],*p1=buf,*p2=buf;
int read()
{
	int x=0; char ch=getchar();
	while ( ch>'9' || ch<'0' ) ch=getchar();
	while ( ch<='9' && ch>='0' ) x=x*10+ch-48,ch=getchar();
	return x;
}
void write( int x ) { if(x<0) putchar(45); if ( x>9 ) write(x/10); putchar(x%10+48); }
void swap( ll &a,ll &b ) { a^=b; b^=a; a^=b; }

const int N=2100000;
const ll Mod=998244353,G=3,InvG=332748118;
int n,m,rev[N];
ll f[N],g[N],Invn;

ll power( ll a,ll b=Mod-2 )
{
	ll res=1;
	for ( ; b; b>>=1,a=a*a%Mod )
		if ( b&1 ) res=res*a%Mod;
	return res;
}

void NTT( ll *f,bool fl )
{
	int i,k,len,l;
	for ( i=0; i<n; i++ ) 
		if ( i<rev[i] ) swap( f[i],f[rev[i]] );
	for ( k=2; k<=n; k<<=1 )
	{
		len=k>>1; ll nwG=power( fl ? G : InvG,(Mod-1)/k );
		for ( i=0; i<n; i+=k )
		{
			ll buf=1;
			for ( l=i; l<i+len; l++ )
			{
				ll tmp=buf*f[len+l]%Mod;
				f[len+l]=f[l]-tmp; 
				if ( f[len+l]<0 ) f[len+l]+=Mod;
				f[l]=f[l]+tmp;
				if ( f[l]>=Mod ) f[l]-=Mod;
				buf=buf*nwG%Mod;
			}
		}
	}
}

int main()
{
	n=read(); m=read(); int i;
	for ( i=0; i<=n; i++ ) f[i]=read();
	for ( i=0; i<=m; i++ ) g[i]=read();
	
	for ( m+=n,n=1; n<=m; n<<=1 );
	for ( i=0; i<n; i++ ) rev[i]=(rev[i>>1]>>1)|((i&1) ? n>>1 : 0);
	NTT( f,1 ); NTT( g,1 );	
	for ( i=0; i<n; i++ ) f[i]=f[i]*g[i]%Mod;
	NTT( f,0 );	Invn=power(n);
	for ( i=0; i<=m; i++ )
		write((int)(f[i]*Invn%Mod)),putchar(32);

	return 0;
}

倍增FFT

目的：给定 $\prod_{i=1}^k(x+i)$ 的各项系数，求 $\prod_{i=k+1}^{2k}(x+i)$ 的各项系数。

令 $F(x)=\prod_{i=1}^k (x+i)=\sum_{i=0}^k c_i\cdot x^i, G(x)=\prod_{i=k+1}^{2k} (x+i)$ ，那么有

\[\begin{aligned} G(x)=F(x+k)&=\sum_{i=0}^kc_i\cdot (x+k)^i\\\\ &=\sum_{i=0}^kc_i\cdot \sum_{j=0}^i\binom{i}{j}k^{i-j}x^j\\\\ &=\sum_{j=0}^k\dfrac{k^{-j}}{j!}\cdot x^j\sum_{i=j}^k(c_i\cdot k^i\cdot i!)\cdot \dfrac{1}{(i-j)!} \end{aligned} \]

把后一个求和符号的式子化成卷积形式即可。

应用

可以用来求 $F(x)=\prod\limits_{i=1}^n(x+i)$ 的各项系数。如果直接用分治 FFT ，那么时间复杂度是 $\mathcal{O}(n\log^2n)$ 。运用倍增 FFT 可以类似快速幂一样做，先求出 $m=\lfloor n/2\rfloor$ 时的 $F$ ，然后用上面的式子求出 $\prod\limits_{i=m+1}^2m$ 的系数，一遍卷积卷起来，如果 $n$ 是奇数再乘上 $(x+n)$ ，复杂度是 $T(n)=T(\frac n 2)+O(n\log n) = O(n\log n)$ .

~~暂时还没有找到例题~~

分治 FFT

模板题给定序列 $g_1\sim g_{n-1}$ ，求 $f_0\sim f_{n-1}$ ，$f_0=1$ .

\[f_i=\sum_{j=1}^ig_jf_{i-j} \]

~~其实我也不太明白为什么一个取模题要FFT~~

思路类似 CDQ 分治，不过不会也没什么要紧的。就是找 $mid$ 两边分治，先算左边，算完之后给右边加贡献，再算右边。

具体可以模一个样例：现在有一个 $g$ 序列 3 1 2 ，一开始 $f$ 序列为 [1,0,0,0] . 先用 $1$ 和 $g$ 去卷积，卷出来的 $3$ 给第二位，$f$ 序列 [1,3,0,0] . 左边算完之后再和 $g$ 卷积，得到 [0,3,10,5,6] ，累加完之后就是 f=[1,3,10,5] ，最后是 $10$ 和 $g$ 卷积，同样做法即可。注意每次都是将卷积完后的序列忽略掉已有的部分再累加。

题目并不卡常，下面的 InitPart 主要作用是不会每次都重新求一遍原根。

//Author: RingweEH
using Poly :: NTT;
using Poly :: Poly_Init;
using Poly :: Poly_InitPart;
int n,F[M],G[M],ans[M],H[M];

void CDQ_NTT( int l,int r )
{
	if ( l+1>=r ) return;
	int mid=(l+r)>>1,len=r-l,i; CDQ_NTT(l,mid);
	Poly_InitPart(len);
	for ( i=0; i<len; i++ ) G[i]=H[i];
	for ( i=l; i<mid; i++ ) F[i-l]=ans[i];
	for ( i=mid; i<r; i++ ) F[i-l]=0;
	NTT( F,1 ); NTT( G,1 );
	for ( int i=0; i<len; i++ ) F[i]=1ll*F[i]*G[i]%Mod;
	reverse(F+1,F+len); NTT( F,0 );
	for ( i=mid; i<r; i++ ) bmod(ans[i]+=F[i-l]);
	CDQ_NTT(mid,r);
}

int main()
{
	n=read();
	for ( int i=1; i<n; i++ ) H[i]=read();
	Poly_Init(n); ans[0]=1; CDQ_NTT(0,Poly::lim);
	for ( int i=0; i<n; i++ ) printf( "%d ",ans[i] );

	return 0;
}

任意模数NTT

用于解决模数没有原根的情况。这是其中一种做法，即取三个有原根的模数 NTT ，（保证其乘积要比最终结果大）然后再合并。但是这样会爆 long long ，__int128 看上去也很不道德，所以需要 CRT 。

具体来说，假设当前这一位的答案是 $x$ ，三个模数是 $P_1,P_2,P_3$ ，那么有

\[x\equiv x_i\pmod{P_i},i=1,2,3 \]

先合并前两个：

\[x_1+k_1P_1\equiv x_2=>k_1\equiv \dfrac{x_2-x_1}{P_1}\pmod{P_2} \]

于是这里就有 $x\equiv x_1+k_1P_1\pmod{P_1P_2}$ ，令其为 $x_4$ ，同样有

\[x_4+k_4P_1P_2\equiv x_3=>k_4=\dfrac{x_3-x_4}{P_1P_2}\pmod{P_3} \]

事实上没那么复杂，也就是把原来的数组手写一个三模数结构体就好了。~~但是我就是调了半天~~ 模板题

//Author: RingweEH
inline int power( int a,int b,int Mod ) { int res=1; for (;b;b>>=1,a=1ll*a*a%Mod) if (b&1) res=1ll*a*res%Mod; return res; }
inline int Get_Inv( int x,int Mod ) { return power(x,Mod-2,Mod); }
inline int pmod( int x,int Mod ) { return x+=x>>31&Mod; }
const int Mod1=998244353,Mod2=1004535809,Mod3=469762049,Gn=3,M=4e5+10;
const ll Mod12=1ll*Mod1*Mod2;
const int Inv1=Get_Inv(Mod1,Mod2),Inv2=Get_Inv(Mod12%Mod3,Mod3);
int Mod;
struct ModInt
{
	int x1,x2,x3;
	ModInt( int _x1=0,int _x2=0,int _x3=0 ) : x1(_x1),x2(_x2),x3(_x3) {}
	ModInt operator + ( ModInt t ) 
	{ return ModInt( pmod(x1+t.x1-Mod1,Mod1),pmod(x2+t.x2-Mod2,Mod2),pmod(x3+t.x3-Mod3,Mod3) ); }
	ModInt operator - ( ModInt t ) 
	{ return ModInt( pmod(x1-t.x1,Mod1),pmod(x2-t.x2,Mod2),pmod(x3-t.x3,Mod3) ); }
	ModInt operator * ( ModInt t ) 
	{ return ModInt( 1ll*x1*t.x1%Mod1,1ll*x2*t.x2%Mod2,1ll*x3*t.x3%Mod3 ); }
	int Merge()
	{
		ll t1=1ll*(x2-x1+Mod2)%Mod2*Inv1%Mod2*Mod1+x1;
		ll t2=(x3-t1%Mod3+Mod3)%Mod3; t2=t2*Inv2%Mod3*(Mod12%Mod)%Mod; t2=t2+t1%Mod; t2%=Mod;
		return t2;
	}
}rt[M];
int lim,Lg,rev[M];
void Poly_Init( int n )
{
	for (lim=1,Lg=0 ; lim<=n; lim<<=1,Lg++ );
	for ( int i=0; i<lim; i++ ) rev[i]=(rev[i>>1]>>1) | ((i&1)<<(Lg-1));
	for ( int i=1; i<lim; i<<=1 )
	{
		ModInt nw(power(Gn,(Mod1-1)/(i<<1),Mod1),power(Gn,(Mod2-1)/(i<<1),Mod2),
			power(Gn,(Mod3-1)/(i<<1),Mod3));
		rt[i]=ModInt(1,1,1);
		for ( int j=1; j<i; j++ ) rt[i+j]=rt[i+j-1]*nw;
	}
}

void NTT( ModInt *f,int opt )
{
	int i,j,k,len; ModInt t1,t2;
	for ( i=0; i<lim; i++ ) if ( i>rev[i] ) swap( f[i],f[rev[i]] );
	for ( i=1; i<lim; i<<=1 )
		for ( j=0; j<lim; j+=i<<1 )
			for ( k=0; k<i; k++ )
			{
				t1=f[j+k]; t2=rt[i+k]*f[i+j+k];
				f[j+k]=t1+t2; f[i+j+k]=t1-t2;
			}	if ( opt ) return; 
	ModInt invn=ModInt(Get_Inv(lim,Mod1),Get_Inv(lim,Mod2),Get_Inv(lim,Mod3));
	for ( i=0; i<lim; i++ ) f[i]=f[i]*invn;
}

另一种做法是拆系数 FFT ，也就是将系数 $a_i$ 拆成 $p_iM+q_i$ 的形式，提出系数之后每个多项式会被拆成两个， $7$ 次FFT解决问题。 ~~口胡完毕~~

参考文献

Command_Block : FFT NTT

JKLover : 倍增FFT

以及某些题目的题解区。~~懒得找了~~

posted @ 2021-01-21 15:48 MontesquieuE 阅读(497) 评论(0) 编辑收藏举报

刷新页面返回顶部

\(p\)	\(g\)
\(998244353=119\cdot 2^{23}+1\)	\(3\)
\(2281701377=17\cdot 2^{27}+1\)	\(3\)
\(1004535809=479\cdot 2^{21}+1\)	\(3\)

Amaurëa.

FFT & NTT 学习笔记

FFT

前置知识

DFT & IDFT 思想

单位根

FFT

具体实现

预处理单位根 & 合并

蝴蝶变换

三次变两次

模板

NTT

前置知识

原根

具体实现

倍增FFT

应用

分治 FFT

任意模数NTT

参考文献

公告