NOIP2018 提高组题解
Day1-T1 铺设道路(road)
给定一个长为 \(n\) 的数组 \(d\) ,每次可以选择一段连续区间 \([L,R]\) 并全部加一。问最少几次能将整个数组变成 \(0\) .
\(1\leq n\leq 1e5,0\leq d_i\leq 1e4\)
Thoughts & Solution
一个很显然的想法是,如下图将所有的凹陷部分以尽可能连续的横向方块填充:(数据为样例)
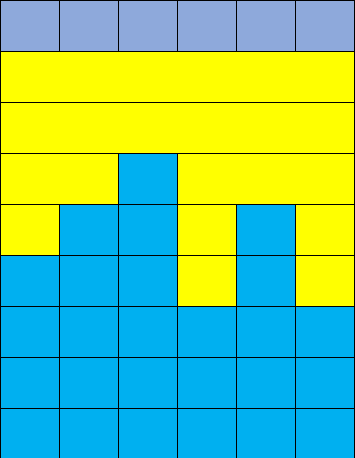
(图中最上面一行为地面,黄色部分每一块就是一次填充)很显然这样就是最优方案。
实现也很简单:从右往左遍历,如果当前 \(a[i]<a[i-1]\) ,就相当于结束掉了上一个横条,不用动;如果当前 \(a[i]>a[i-1]\) ,说明又要新建 \(a[i]-a[i-1]\) 个横条,计入答案即可。
复杂度 \(\mathcal{O}(n)\) .
//Author: RingweEH
int n,las,ans;
int main()
{
n=read(); las=ans=0;
for ( int i=1,x; i<=n; i++ )
{
x=read();
if ( x>las ) ans+=(x-las);
las=x;
}
printf( "%d\n",ans );
return 0;
}
Day1-T2 货币系统(money)
有 \(n\) 种不同面值的货币,第 \(i\) 种面值为 \(a[i]\) ,每种无限张。
将一个有 \(n\) 种货币、面值数组为 \(a[1\dots n]\) 的货币系统记作 \((n,a)\) .称两个货币系统 \((n,a),(m,b)\) 等价,当且仅当对于任意 \(x\in N\) ,要么均能被两个货币系统表示出来,要么不能被任何一个表示。
给定一个货币系统 \((n,a)\) ,找到一个最小的 \(m\) 使得存在货币系统 \((m,b)\) 与 \((n,a)\) 等价。
\(n\leq 100,a[i]\leq 25000\) .
Thoughts & Solution
感觉这道题重点不是 DP 是证明……比如你考场的时候,想到了这个解法,但是如果用了怕结论是错的,不用又怕错失正解,其实是很纠结的……所以我这里就写一写证明过程吧,其实也不难。
有一个很显然的想法:答案中的系统方案一定是由原先的系统方案去掉若干种货币得到
事实上这就是正确的。
Proof
令给出的系统中的货币面值为 \(A\) 集合,需要得到的货币面值为 \(B\) 集合。
引理:\(A\) 集合中不能被其他数组成的数一定会在 \(B\) 集合中出现。
引理的证明:设有一个数 \(x\in A\) 且不能被 \(A\) 集合中其他数凑出来。 根据等价,如果 \(x\notin B\) ,那么 \(B\) 中的其他数一定能组成 \(x\) .这就说明 \(B\) 中至少存在一个不属于 \(A\) 集合且不能被 \(A\) 组合出来的数(不然 \(A\) 集合就一定能合成 \(x\) ),那么这个数本身不属于 \(A\) 能组成的范畴,却属于 \(B\) 能组成的范畴,就不符合题意了。所以 \(x\in B\) ,引理正确性证毕。
那么现在我们需要证明:\(B\subseteq A\) .
仍然采用反证法。设存在一个数 \(x\) 满足 \(x\in B\) 且 \(x\notin A\) .
根据题意,显然 \(x\) 能被 \(A\) 中若干个 \(a_1,a_2,\dots ,a_k\) 组成(假定这些数不能被拆分成 \(A\) 中其他的数,如果能拆分就直接拿拆分方案替换即可)。根据引理,这些数都属于 \(B\) ,也就是说,\(B\) 完全可以通过这些数组成 \(x\) ,那么 \(B\) 中再存在一个 \(x\) 显然就是多余的,和 \(B\) 集合最小的要求不符。
Q.E.D.
接下来的事情就非常简单了。我们只需要考虑 \(A\) 集合中哪些数是多余的就好了。
题目暗示:现在网友们打算 简化 一下货币系统。这说明就是在原基础上去掉某些数(
这个事情可以一次 DP 解决。观察到 \(a[i]\) 的范围只有 \(25000\) ,那么可以直接设 \(f[i]\) 表示 \(i\) 这个数能否被前面已经出现过的 \(a[j]\) 组成。
- 如果枚举到 \(a[i]\) 时,\(f[a[i]]=1\) ,那么直接计入答案并跳过即可;
- 如果没有,那么枚举所有的 \(j=a[i]\sim mx\) ,\(f[j]|=f[j-a[i]]\) (就是用 \(j-a[i]\) 和 \(a[i]\) 组成 \(j\) ,枚举范围中的 \(mx\) 表示所有 \(a[i]\) 中的最大值)
完结散花 (。・∀・)ノ゙
注意题目中给出的 \(a\) 数组不一定有序,要记得排序。
//Author: RingweEH
const int N=110,M=25010;
int n,a[N],f[M];
int main()
{
int T=read();
while ( T-- )
{
n=read();
for ( int i=1; i<=n; i++ )
a[i]=read();
sort( a+1,a+1+n ); int mx=a[n];
memset( f,0,sizeof(f) ); f[0]=1; int ans=n;
for ( int i=1; i<=n; i++ )
{
if ( f[a[i]] ) { ans--; continue; }
for ( int j=a[i]; j<=mx; j++ )
f[j]|=f[j-a[i]];
}
printf( "%d\n",ans );
}
}
Day1-T3 赛道修建(track)
一棵带边权的树,在树上选出 \(m\) 条互不相交的链(点可以重合,但是边不能重合),使得 \(m\) 条链中最短的链最长。
\(2\leq n\leq 5e4,1\leq m\leq n-1\) .
Thoughts & Solution
看到“最短的链最长”就很容易想到二分。二分一个最短链长,然后看能否组成至少 \(m\) 条互不相交的长度不小于 \(mid\) 的链即可。
现在的问题就是如何判定了。我们定义“一条链对答案有贡献”表示,这条链的链长不小于当前枚举的最小值。
考虑一条链是如何被组成的。
对于一棵子树 \(u\) ,显然通过根节点 \(u\) 向上拼接的链最多只能有一条,因此让链尽可能在子树内贡献更多的答案而不是往上走显然是不会更劣的。
那么正解就来了。我们可以用 DP 处理出这个向上走的链长。令 \(f[u]\) 为以 \(u\) 为根的子树中,最优的不完整链长(就是通过根节点向上拼接的链)(完整的部分就是链长 \(\ge mid\) 的,已经贡献到答案里面去了)。
暂时不考虑根节点 \(u\) ,对于 \(u\) 的所有儿子,如果能单独贡献就直接计入答案。否则,尝试两两合并这些子树中向上走的链(因为点是可以重合的,在根节点合并多少都没有关系),如果长度 \(\ge mid\) 就一样计入答案。最后剩下的链中,取一条最长的(也就最容易产生贡献)走过根节点,计入 \(f[u]\) 并往上走。
具体实现就可以直接对子树中所有的链长升序排序,然后倒序枚举,对于每一条链找一条 能匹配出 \(\ge mid\) 的链中最短的一条链 进行拼接,计入答案即可。最后把剩下的链中的最大值转移给 \(f[u]\) .
但是要注意一点,你贪心两两匹配子树中的链,最后得到的只是“能匹配的最大对数”,而不是“能匹配的最优方案”。所以要在得到这个最大对数之后,再来一次二分,找一个最大的 mid 使得 去掉这个mid之后,剩下的部分仍然能匹配出这个最大对数。那么最后得到的 mid 就是要计入 \(f[u]\) 中的值。
//Author: RingweEH
const int N=5e4+10;
struct edge
{
int to,nxt,val;
}e[N<<1];
int n,m,tot=0,head[N],res,f[N];
vector<int> son[N];
void add( int u,int v,int w )
{
e[++tot].to=v; e[tot].nxt=head[u]; head[u]=tot; e[tot].val=w;
e[++tot].to=u; e[tot].nxt=head[v]; head[v]=tot; e[tot].val=w;
}
int get_pair( int u,int pos,int num,int lim ) //在去掉pos这个数之后,所能匹配出的最大对数
{
int now_res=0,l=0;
for ( int r=num-1; r; r-- )
{
r-=(r==pos);
while ( l<r && son[u][l]+son[u][r]<lim ) l++;
l+=(l==pos);
if ( l>=r ) break;
now_res++; l++;
}
return now_res;
}
void dfs( int u,int fa,int lim )
{
son[u].clear();
for ( int i=head[u]; i; i=e[i].nxt )
{
int v=e[i].to; if ( v==fa ) continue;
dfs( v,u,lim ); f[v]+=e[i].val;
if ( f[v]>=lim ) res++;
else son[u].push_back( f[v] );
}
//将所有子树上来的链拉到根节点,并判断是否可以独自产生贡献,如果不能那么放入配对序列
int num=son[u].size(); sort( son[u].begin(),son[u].end() );
int l=0,r=num-1,cnt=0;
for ( ; r; r-- )
{
while ( l<r && son[u][l]+son[u][r]<lim ) l++;
if ( l>=r ) break;
cnt++; l++;
}
//配对过程,cnt就是得到的最大对数。
res+=cnt;
if ( cnt*2==num ) { f[u]=0; return; } //全配完了,不需要再往上转移
l=0; r=num-1; int now_res=0;
while ( l<=r )
{
int mid=(l+r)>>1,now=get_pair( u,mid,num,lim );
if ( now==cnt ) now_res=mid,l=mid+1;
else r=mid-1;
}
//二分转移上去的最大链长,使得剩下的链仍能满足最大匹配
f[u]=son[u][now_res];
}
bool check( int mid )
{
memset( f,0,sizeof(f) );
res=0; dfs( 1,0,mid );
return (res>=m) ? 1 : 0;
}
int main()
{
freopen( "track.in","r",stdin ); freopen( "track.out","w",stdout );
n=read(); m=read(); int r=0;
for ( int i=1,u,v,w; i<n; i++ )
u=read(),v=read(),w=read(),add( u,v,w ),r+=w;
int l=0,ans=0; r=r/m;
while ( l<=r )
{
int mid=(l+r)>>1;
if ( check(mid) ) ans=mid,l=mid+1;
else r=mid-1;
}
printf( "%d\n",ans );
fclose( stdin ); fclose( stdout );
return 0;
}
Day2-T1 旅行(travel)
给定一个 \(n\) 点 \(m\) 边无向连通图,不存在重边和自环。从任意一点出发,每次可以走向一个没去过的点或者按第一次访问当前点的路径回退。求一个字典序最小的遍历序列。
\(n\leq 5e3\) , \(m=n\) 或 \(m=n-1\) .
Thoughts & Solution
这道题的关键显然在于数据范围。\(m=n\) 或 \(m=n-1\) ,就相当于是 一棵树或者基环树 。
60pts 树
对于一棵树,显然只要选定了起点,然后每次遍历子树时从小到大遍历即可。由于字典序要小,所以从 1 开始,一次 DFS 就能解决。
时间复杂度 \(\mathcal{O}(n\log n)\) .(因为要排序)
40pts 基环树
仔细想想就会发现,由于 不是后退就是新点 ,所以易知无论图长什么样,我们都只会遍历到 \(n-1\) 条边。所以其实就算有 \(n\) 条边也是有一条没用的。那不妨枚举删掉一条,然后就可以按照树的方法跑了。
复杂度是 \(\mathcal{O}(n^2)\) (排序在初始化就可以做掉,没必要放进 DFS 里面去),大概是 \(2e7\) 左右。如果觉得不稳可以加剪枝,如果当前已经比答案劣了直接退出。
注意:删边要保证连通性,只要判最后 vis 了几个点就好了,没必要再写个找环;写剪枝(和最优解比较)的时候,只要前面有一次比最优解优,那么后面都不用判了,这点要加个标记。
大常数选手由于写了太多 STL 所以 ACWing 上要吸氧。
C++ 之父:STL常数大那是你编译器不行(
//Author: RingweEH
const int N=5010;
int n,m,pos=0,cnt=0,better;
bool vis[N];
vector<int> g[N],path,ans;
pair<int,int> edge[N];
void dfs( int u )
{
if ( (!better) && (u>ans[cnt]) ) return;
if ( !better && u<ans[cnt] ) better=1;
vis[u]=1; path.push_back( u ); cnt++;
for ( int i=0; i<g[u].size(); i++ )
{
int v=g[u][i];
if ( vis[v] ) continue;
if ( (u==edge[pos].first) && (v==edge[pos].second ) ) continue;
if ( (v==edge[pos].first) && (u==edge[pos].second ) ) continue;
dfs( v );
}
}
int main()
{
freopen( "travel.in","r",stdin ); freopen( "travel.out","w",stdout );
n=read(); m=read();
edge[0].first=edge[0].second=-1;
for ( int i=1,u,v; i<=m; i++ )
{
u=read(),v=read(),g[u].push_back( v ),g[v].push_back( u );
edge[i].first=u; edge[i].second=v;
}
for ( int i=1; i<=n; i++ )
sort( g[i].begin(),g[i].end() );
for ( int i=1; i<=n; i++ )
ans.push_back( 60000 );
if ( m==n )
{
for ( int i=1; i<=m; i++ )
{
memset( vis,0,sizeof(vis) ); path.clear();
pos=i; cnt=better=0; dfs( 1 );
if ( cnt==n ) ans=path;
}
}
else
{
dfs( 1 );
if ( cnt==n ) ans=path;
}
for ( int i=0; i<ans.size(); i++ )
printf( "%d ",ans[i] );
fclose( stdin ); fclose( stdout );
return 0;
}
Day2-T2 填数游戏(game)
给定一个 \(n\times m\) 的矩形表格,要在每个格子里面填入 0/1.以下是限制。
- 用一个格子的行列坐标来表示格子,坐标从 0 开始编号
- 合法路径起点是 \((0,0)\) 终点是 \((n-1,m-1)\) ,每次只能向下移动一格或者向上移动一格,向下走是
D向上走是R. - 对于一条合法路径 \(P\) ,用字符串 \(w(P)\) 表示其走向,用 \(s(P)\) 表示路径经过的所有数组成的序列
- 合法的填数方案满足:对于两条合法路径 \(P_1,P_2\) ,如果 \(w(P_1)>w(P_2)\) ,那么 \(s(P_1)\leq s(P_2)\) .(大小按字典序排)
求填数方案数对 \(1e9+7\) 取模的结果。\(n\leq 8,m\leq 1e6\) .
Thoughts & Solution
看 你谷题解 吧……
Day2-T3 保卫王国(defense)
给定一棵 \(n\) 点树,在节点上驻扎军队有如下条件:
- 由道路直接连接的两座城市中至少要有一座城市驻扎军队。
- 在编号为 \(i\) 的城市中驻扎军队的花费是 \(p_i\)
给出 \(m\) 次询问,每次规定其中两座城市是否驻扎,求这种情况下的最小花费,无解输出 -1 .
Thoughts & Solution
一看上去并没有带修,但是 “规定是否驻扎” 可以等价于给权值加上/减去 \(\infin\) 。
令 \(f[u][0]\) 为 \(u\) 不放军队的子树最小代价,\(f[u][1]\) 类似。
套树剖,令 \(g[u][0]=\sum\limits_{v\neq wson[u]}f[v][0],g[u][1]=a[u]+\sum\limits_{v\neq wson[u]}\min(f[v][0],f[v][1])\) .
所以这里的矩阵乘法要搞成 \(\min\) 的,或者也可以把状态设成最大化不用的权值。
然后就直接树剖/LCT即可。
松不动松不动松不动 /dk
//Author: RingweEH
//LOJ#2955. 「NOIP2018」保卫王国
#define ls tr[x][0]
#define rs tr[x][1]
const int N=1e5+10;
const ll INF=2e15;
int n,m,head[N],tot,fa[N],tr[N][2],w[N];
ll val[N][2];
map<int,int> mp[N];
struct Matrix
{
ll mat[2][2];
ll get_mx() { return max(mat[0][0],mat[1][0]); }
Matrix( ll x=-INF,ll y=-INF ) { mat[0][0]=mat[0][1]=x; mat[1][0]=y; mat[1][1]=-INF; }
void Set( ll x=-INF,ll y=-INF ) { mat[0][0]=mat[0][1]=x; mat[1][0]=y; mat[1][1]=-INF; }
}g[N];
Matrix operator * ( Matrix A,Matrix B ) {}
struct Edge { int to,nxt; }e[N<<1];
void Adde( int u,int v ) { e[++tot].to=v; e[tot].nxt=head[u]; head[u]=tot; }
bool IsRoot( int x ) { return (tr[fa[x]][0]==x) || (tr[fa[x]][1]==x); }
void Pushup( int x )
{
g[x].Set(val[x][0],val[x][1]);
if ( ls ) g[x]=g[ls]*g[x];
if ( rs ) g[x]=g[x]*g[rs];
}
void Rotate( int x )
{
int y=fa[x],z=fa[y]; bool kid=(tr[y][1]==x);
if ( IsRoot(y) ) tr[z][tr[z][1]==y]=x;
tr[y][kid]=tr[x][kid^1]; fa[tr[x][kid^1]]=y; tr[x][kid^1]=y; fa[y]=x; fa[x]=z;
Pushup(y); Pushup(x);
}
void Splay( int x )
{
int y,z;
while ( IsRoot(x) )
{
y=fa[x]; z=fa[y];
if ( IsRoot(y) )
Rotate( ((tr[y][1]==x)^(tr[z][1]==y)) ? x : y );
Rotate(x);
}
}
void Access( int x )
{
for ( int y=0; x; y=x,x=fa[x] )
{
Splay(x);
if ( rs ) val[x][0]+=g[rs].get_mx(),val[x][1]+=g[rs].mat[0][0];
if ( y ) val[x][0]-=g[y].get_mx(),val[x][1]-=g[y].mat[0][0];
tr[x][1]=y; Pushup(x);
}
}
void DFS( int u,int fat )
{
fa[u]=fat; val[u][1]=w[u];
for ( int i=head[u]; i; i=e[i].nxt )
{
int v=e[i].to;
if ( v==fat ) continue;
DFS(v,u); val[u][1]+=val[v][0]; val[u][0]+=max(val[v][0],val[v][1]);
}
g[u].Set(val[u][0],val[u][1]);
}
int main()
{
scanf( "%d%d",&n,&m ); char typ[10]; scanf( "%s",typ ); ll sum=0;
for ( int i=1; i<=n; i++ ) w[i]=read(),sum+=w[i];
for ( int i=1,u,v; i<n; i++ )
u=read(),v=read(),Adde(u,v),Adde(v,u),mp[u][v]=mp[v][u]=1;
DFS(1,0);
for ( int i=1; i<=m; i++ )
{
int a=read(),x=read(),b=read(),y=read(); ll lasa,lasb;
if ( mp[a][b]==1 && x==0 && y==0 ) { puts("-1"); continue; }
Access(a); Splay(a); lasa=val[a][x]; val[a][x]=-INF; Pushup(a);
Access(b); Splay(b); lasb=val[b][y]; val[b][y]=-INF; Pushup(b);
ll ans=g[b].get_mx(); printf("%lld\n",sum-ans );
val[b][y]=lasb; Pushup(b);
Access(a); Splay(a); val[a][x]=lasa; Pushup(a);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号