朱刘算法学习笔记

提出问题

首先给出树形图的定义：（可以近似理解为有向图上的生成树）（定义取自训练指南）

• 有向图中定义
• 无环
• 根节点可以到达任意一个节点
• 根节点入度为 0 ，其他节点入度为 1

然后是最小树形图：

• 边权和最小的树形图。

分析问题

算法简介

这个算法名叫 朱-刘算法，根据网上说法是 朱永津-刘振宏 发明的，

1965年,提出最小树形图算法,运用图的收缩与扩张的运算,绘出了在一个有向图中求最小树形图的一个多项式算法,在拟阵交计算上为首创,被称为“朱-刘算法”。

流程

Warning: 以下说明的是 树有根 的情况。

首先放一张 luogu题解 的图：（第二张看上去并不友好，于是拿了第一张）

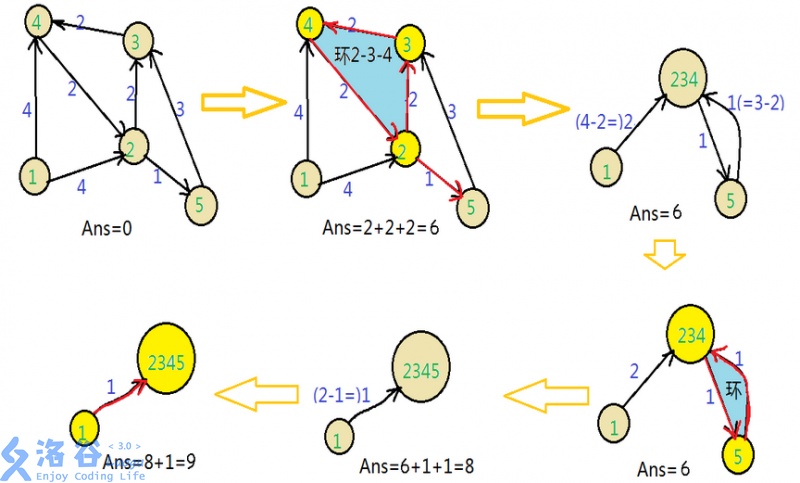
• 首先，每个点的出度可能会有多个，不好考虑，所以按照入度为 \(1\) （非根）这个性质来思考。
• 容易想到，每次对除根外每个点找出权值最小的入边并累计入答案中。
• 判断选出的边是否存在环，如果没有就说明找到了最小树形图，退出。
• 将所有环缩点，构造一个新图，对于原图的每条边：如果这条边在环内，删去；否则，如果该边的终点（指向节点）在环内，将权值修改为（这条边原先的权值-终点在环上的入边权值）
• 重复这个步骤，直到满足无环为止。

正确性证明

• 其实朱刘算法本质是一个反悔贪心
• 对于每个环，显然一定存在一个最优解，只去掉一条边（如果选了两条，把其中一条选回去，答案不会变差）
• 如果你选了新的权值（就是作差过的），相当于去掉环上对应的入边，然后改选了当前这一条。程序里不需要判终点是否在环内，直接把不在环上的点当做一个环处理即可。因为这样修改边权，减去的权值就是原来的边权，就和“选这一条边”的意义是一样的了。
• 每次缩点点数至少会减一，复杂度 \(O(VE)\)

拓展——不定根

这个其实和 多源最短路 之类的解决方法是类似的，考虑对每个点都连到一个虚根 \(rt\) ，\(n\) 条边均由 \(rt\) 指向其他点，并且把边权设置为 (原来的所有边权和 \(sum\) +1) 。然后就可以跑有根的朱刘了。

如果最后跑出来，权值和 \(>2\times sum\) 说明用了两条新的边，但是原图的树形图里面显然不可能存在两个根节点，所以原图是无法形成最小树形图的。

否则就可以根据唯一的一条新加边指向的点确定树形图的根节点，因为它除了 \(rt\) 以外，没有被原图中任何其他节点指向。

解决问题

代码来源：P4716 【模板】最小树形图

如果你需要通过代码更好地理解算法，那么这里提供：

代码变量名称约定
 n,m,rt：题目给出的点数，边数，根节点
 min_pre[],fa[]：每次执行中找到的最小入边的权值，入边的起点
 cnt_cyc,incyc_id[]：环的编号计数，每个点在哪个环里面
 f[]：类似并查集中的最高祖先，找一个点沿着入边往上跳的最终节点

代码实现：

//Author: RingweEH
const int N=110,M=1e4+10,inf=0x3f3f3f3f;
struct edge
{
    int u,v; ll val;
}e[M];
int n,m,rt,cnt_cyc,fa[N],incyc_id[N],f[N],min_pre[N];
ll ans=0;

int ZhuLiu()
{
    while ( 1 )
    {
        cnt_cyc=0;
        for ( int i=1; i<=n; i++ )
            incyc_id[i]=f[i]=0,min_pre[i]=inf;
        //---------------------init----------------------
        for ( int i=1; i<=m; i++ )
            if ( e[i].u!=e[i].v && e[i].val<min_pre[e[i].v] )
                fa[e[i].v]=e[i].u,min_pre[e[i].v]=e[i].val;
        //--------------找每个点的最小入边---------------
        int now=min_pre[rt]=0;
        for ( int i=1; i<=n; i++ )
        {
            if ( min_pre[i]==inf ) return 0;    //孤立点特判
            ans+=min_pre[i];        //不管如何先把边权加进去就好了
            for ( now=i; now!=rt && f[now]!=i && !incyc_id[now]; now=fa[now] )
                f[now]=i;   //从i不断往选定的入边跳，途中不能往其他已经判定的环里面跳
            if ( now!=rt && !incyc_id[now] )    
            //看上面循环的判断条件，只满足了 f[now]==i ，也就是形成了环
            {
                incyc_id[now]=++cnt_cyc;
                for ( int v=fa[now]; v!=now; v=fa[v] )
                    incyc_id[v]=cnt_cyc;
            }
        }
        if ( !cnt_cyc ) return 1;
        //-----------------------找环----------------------
        for ( int i=1; i<=n; i++ )  //给不在环中的点也赋一个标号，方便判断
            if ( !incyc_id[i] ) incyc_id[i]=++cnt_cyc; 
        for ( int i=1; i<=m; i++ )
        {
            int las=min_pre[e[i].v];    //e[i].v的最小入边权
            e[i].u=incyc_id[e[i].u]; e[i].v=incyc_id[e[i].v];   //缩成同一个点，也就是环编号
            if ( e[i].u!=e[i].v )  e[i].val-=las;   //如果不在同一个环里面就修改边权
        }
        n=cnt_cyc; rt=incyc_id[rt]; //缩点完成后的点数就是环的个数，并更新根节点编号。
    }
}

int main()
{
    n=read(); m=read(); rt=read();
    for ( int i=1; i<=m; i++ )
        e[i]=(edge){read(),read(),read()};
    
    if ( ZhuLiu() ) printf( "%lld",ans );
    else printf( "-1\n" );
    return 0;
}

习题

UVA11865 Stream My Contest

题意：你需要花费不超过 \(cost\) 元来搭建一个比赛网络。网络中有 \(n\) 台机器，编号 \(0\sim n-1\) ，0 为服务机，其他均为客户机。一共有 \(m\) 条可以使用的网线，数据只能从 \(u_i\to v_i\) 单向传递，带宽 \(b_i\) Kbps，费用 \(c_i\) 元。每台客户机应当恰好从一台机器接受数据，服务器不接受数据。最大化最小带宽。

思路：如果要最大化最小带宽，很容易想到二分最小带宽并去掉所有小于带宽的边。而让所有客户机都能收到，其实就是服务机要能到达每个客户机，要是对性质熟悉的话就很容易想到树形图。那么对于二分的判定，只需要求出从 0 出发的最小树形图，判断权值和是否超过给定 \(cost\) 即可。

//Author: RingweEH
int ZhuLiu()
{
    ans=0;
    while ( 1 )
    {
        cnt_cyc=0;
        for ( int i=1; i<=n; i++ )
            incyc_id[i]=f[i]=fa[i]=0,min_pre[i]=inf;
            
        for ( int i=1; i<=newm; i++ )
            if ( e[i].u!=e[i].v && e[i].val<min_pre[e[i].v] )
                fa[e[i].v]=e[i].u,min_pre[e[i].v]=e[i].val;
                
        int now=min_pre[rt]=0;
        for ( int i=1; i<=n; i++ )
        {
            if ( min_pre[i]==inf ) return -1;
            ans+=min_pre[i];
            for ( now=i; now!=rt && f[now]!=i && !incyc_id[now]; now=fa[now] )
                f[now]=i;   
            if ( now!=rt && !incyc_id[now] )    
            {
                incyc_id[now]=++cnt_cyc;
                for ( int v=fa[now]; v!=now; v=fa[v] )
                    incyc_id[v]=cnt_cyc;
            }
        }
        if ( !cnt_cyc ) break;

        for ( int i=1; i<=n; i++ )  
            if ( !incyc_id[i] ) incyc_id[i]=++cnt_cyc; 
        for ( int i=1; i<=newm; i++ )
        {
            int las=min_pre[e[i].v];    
            e[i].u=incyc_id[e[i].u]; e[i].v=incyc_id[e[i].v];  
            if ( e[i].u!=e[i].v )  e[i].val-=las;  
        }
        n=cnt_cyc; rt=incyc_id[rt]; 
    }
    return ans;
}

bool check( int x )
{
    rt=1; n=savn; newm=0;
    for ( int i=1; i<=m; i++ )
        if ( save[i].wide>=x ) e[++newm]=save[i];
    int answer=ZhuLiu();
    return answer!=-1 && answer<=cost;
}

int main()
{
    int T=read(); n=-1;
    for ( int cas=1;cas<=T; cas++)
    {
        n=savn=read(); m=read(); cost=read(); int mxwid=0;
        for ( int i=1; i<=m; i++ )
        {
            e[i].u=read()+1,e[i].v=read()+1; e[i].wide=read(); e[i].val=read();
            mxwid=max( mxwid,e[i].wide ); save[i]=e[i];
        }
        
        int l=0,r=mxwid,res=-1;
        while ( l<=r )
        {
            int mid=(l+r)>>1; 
            if ( check(mid) ) l=mid+1,res=mid;
            else r=mid-1;
        }
        if ( res==-1 ) { printf( "streaming not possible.\n" ); continue; }
        printf( "%d kbps\n",res );
    }
}

参考

墨染空大佬的博客