文化课の疑难杂症

Start Recording：20201117

有时候会在机房里写作业，记录在这里。

语文

• 要学会用文学语言而不是信息语言，不要写个文写得跟题解一样
• 阅读题分析感情啊什么的 不要忘记写内容梗概 ……名著阅读也是。

数学

组合

1. 路上编号1~10的十盏路灯，关3盏，但是不能相邻的2或3盏，两端不关，问方案

   \(C_6^3\) 如何计算？ ——7盏插3

2. （2020浙江 9+1 联盟11月联考，7）弦图由四个全等直角三角形和一个正方形构成，五种颜色染色，相邻不同色，方案数为 420 180

   题目没有给出什么样的方案是等价的，我自动默认是旋转等价，就挂了……

   五色：\(120\)

   四色：\(C_2^1\times C_5^1\times P_4^3=240\)

   三色：\(P_5^2\times C_3^1=60\)

三角函数

1. 三角函数常见技巧/推导：

   求导：

   \[y=\sin x,y'=\cos x\\ y=\cos x,y'=-\sin x\\ y=\tan x,y'=\sec^2 x\\ y=\cot x,y'=-\csc^2x\\ y=\sec x,y'=\sec x\tan x\\ y=\csc x,y'=-\csc x\cot x\\ \]

   辅助角：

   \[a\sin x+b\cos x=\sqrt{a^2+b^2}\sin\Big(x+\arctan \frac{b}{a}\Big) \]

2. 三角函数求最小正周期，多项 \(\sin,\cos\) 的时候直接看最大的那个，不要老想着推式子…… 虽然一般第二小题就会让你推

3. 不要再犯向左右移动图象去动常数的sb错误了……

4. 遇到类似 \(\sin(\alpha+t)=\cos(\alpha+t')+\cos(\alpha-t')\) ，先和差公式化开，然后转变成 \(\tan\) 的表达式，再用容易求的角关联 \(t,t'\) . （事实上齐次式都能用 \(\tan\) 化吧）

5. 最简单三角方程：

   \[\begin{aligned} \sin x&=a=>x=k\pi+(-1)^k\arcsin a\\\\ \cos x&=a=>x=2k\pi\pm\arccos a\\\\ \tan x&=a=>x=k\pi+\arctan a\\\\ \cot x&=a=>x=\text{arccot }a+k\pi \end{aligned} \]

   其他只需要化成最简方程然后带入就好了。

6. 和差化积典型应用：

   \[\dfrac{2\sin(x_2-x_1)}{\sin x_2-\sin x_1}=\dfrac{4\sin\dfrac{x_2-x_1}{2}\cos\dfrac{x_2-x_1}{2}}{2\cos\dfrac{x_2+x_1}{2}\sin\dfrac{x_2-x_1}{2}}=\dfrac{2\cos\dfrac{x_2-x_1}{2}}{\cos\dfrac{x_2+x_1}{2}} \]

   也不要总是拘泥于和差角啊。

7. 一些简要结论：

   设 \(f(x),g(x)\) 对任意 \(x\in R\) 均有 \(-\dfrac{\pi}{2}<f(x)\pm g(x)<\dfrac{\pi}{2}\) ，那么有 \(\cos f(x)>\sin g(x)\) 。

   \[\cos(\cos x)>\sin(\sin x),\sin(\cos x)<\cos(\sin x)\\\\ \sin(\sin(\sin x))<\sin(\cos(\cos x))<\cos(\cos(\cos x)) \]

   NB总结

数列

1. 递推求通项的方法：

   • 构造特殊数列，利用特殊数列的通项求解
   • 迭代法，适当变形之后建立一般项和初始的联系
   • 不动点，分式线性递推数列 \(a_{n+1}=\dfrac{Ca_n+D}{Aa_n+B}(A\neq 0)\) （不动点就是让分式 \(f(x)=x\) 所得到的的取值）
   • 特征方程：\(a_1=C,a_{n+1}=pa_n+qa_{n-1}+r(p\neq 0)\)

2. 概念问题：有穷数列无极限。

3. 无穷等比数列求和：\(\lim\limits_{n\to\infin}S_n=\dfrac{a_1}{1-q}(\lim 1-\lim q^n)=\dfrac{a_1}{1-q}(0<|q|<1)\) ；基本有限等比数列求和：裂项，错位，分组。

极限

1. 算不出来具体值的时候不妨试试用大小于限定出确切值。

2. \(\lim\limits_{n\to\infin}n^{\frac 1n}=\lim e^{\ln n\cdot (1/n)}=e^{\lim \ln n/n}=e^{\lim (1/n)}=e^0=1\) .

3. 极限有关性质

   \(\lim\limits_{x\to x_0}f(x)=A\) 的充要是 \(\lim\limits_{x\to x_0^+}f(x)=\lim\limits_{x\to x_0^-}f(x)=A\) .

   \(y=f(u),u=\varphi(x),\lim\limits_{x\to x_0}\varphi(x)=u_0\) ，且在 \(x_0\) 的一个邻域内 \(\varphi(x)\neq u_0\) ，\(\lim\limits_{u\to x_0}f(u)=A\) ，\(\lim\limits_{x\to x_0}f(\varphi(x))=A\) .

   （局部有界性）若 \(\lim\limits_{x\to x_0}f(x)=A\) ，则存在 \(x_0\) 去心邻域 \(\mathring{U}(x_0,\delta)\) 和 \(M>0\) 使得 \(\forall x\in\mathring{U}(x_0,\delta),|f(x)|\leq M\) .

   （保号性） 若 \(\lim\limits_{x\to x_0}f(x)=A,A>0(A<0)\) ，那么存在 \(\delta>0\) 使得 \(\forall x\in\mathring{U}(x_0,\delta)\) ，有 \(f(x)>0(f(x)<0)\) .

4. \(\delta-\varepsilon\) 定义：设函数 \(f(x)\) 在 \(x_0\) 某一去心邻域 \(\mathring{U}(x_0,\delta)\) 内有定义，对 \(\forall \varepsilon>0\) 总存在 \(\delta>0\) ，当 \(0<|x-x_0|<\delta\) 时，有 \(|f(x)-A|<\varepsilon\) 恒成立，则称 \(f(x)\) 当 \(x\to x_0\) 时以 \(A\) 为极限。

5. 收敛准则（夹逼定理）：设 \(f(x),g(x),h(x)\) 在 \(x_0\) 点的去心邻域 \(\mathring{U}(x_0,\delta)\) 内有定义，且满足：对于 \(\forall x\in\mathring{U}(x_0,\delta)\) 有 \(g(x)\leq f(x)\leq h(x)\) ； \(\lim\limits_{x\to x_0}g(x)=\lim\limits_{x\to x_0}h(x)=A\) 。那么 \(\lim\limits_{x\to x_0}f(x)=A\) 。

6. 常见函数导数性质

   \[\arcsin'x =\dfrac 1{\sqrt{1-x^2}};\arccos'x=-\dfrac 1{\sqrt{1-x^2}};\arctan'x=\dfrac 1{1+x^2};\text{arccot}'x=-\dfrac1{1+x^2}\\\\ \ln'x=\dfrac 1x;(e^x)'=e^x;\log_a'x=\dfrac 1x\log_a e;(a^x)'=a^x\ln a \]

7. 基本求导法则

   \[\left(\dfrac{u(x)}{v(x)}\right)'=\dfrac{u'(x)v(x)-u(x)v'(x)}{v(x)^2}(v(x)\ne 0) \]

   若 \(u=\varphi(x),u'_x=\varphi'(x);y=f(x),y'_u=f'(u)\) ，那么 \(f'_x[\varphi(x)]=f'(u)\varphi'(x)\) .

   若 \(y=f(x),x=\varphi(y)\) ，\(y\) 在 \(x\) 处连续，\(x\) 在 \(x\) 处导数 \(\neq 0\) ，那么 \(f'(x)=\dfrac 1{\varphi'(y)}\) .

8. \(g(x)=e^xf(x)=>g'(x)=e^xf(x)+e^xf'(x)\)

9. \(\sqrt{2x+1}\) 求导：复合函数 \((f(g(x)))'=g'(x)f'(g(x))\) ，所以 \((\sqrt{2x+1})'=2\cdot\frac12(1+2x)^{-1/2}=\frac1{\sqrt{2x+1}}\) .

函数

1. 函数 \(f(x)=|\sqrt{1-x^2}-ax-b|(a,b\in R)\) ，当 \(x\in[0,1]\) 时，设 \(f(x)_{max}=M(a,b)\) ， \(M(a,b)_{min}=\)

   属于典型代数做傻了的例子=.=

   四分之一圆 \(y=\sqrt{1-x^2},x\in[0,1]\) 上的点到直线 \(l:x+y=1\) 的最大距离为 \(1-\dfrac{\sqrt 2}2=\dfrac{2-\sqrt 2}2\) ，此时圆上点记为 \(P\) ，\((0,1),(1,0)\) 连线和 \(OP\) 的交点记为 \(N\) ，只有过 \(PN\) 中点且平行于 \(l\) 的直线满足条件。当 \(a=-1,b=\dfrac{\sqrt 2+1}2\) 时，\(M(a,b)_{min}\) 为 \(g(x)=\sqrt{1-x^2},x\in[0,1]\) 和 \(h(x)=ax+b=-x+\dfrac{\sqrt 2+1}2\) 的纵向距离，即 \(\dfrac{\sqrt 2-1}2\) .

2. 对于 \(x,y\) 的一次或者二次式，另一边是一个常数的不等式，可以考虑函数图像。

3. 求不等式的时候看似前后两问可以用前面的结论，但是要注意取到 \(\min,\max\) 的极值点可能不是同一个，没法用。

不等式

1. 常见放缩：\(\dfrac 1{\sqrt k}<\dfrac 2{\sqrt{k-1}+\sqrt{k}}=2(\sqrt k-\sqrt{k-1})\) ，\(\dfrac 12\left(\dfrac 1{\sqrt k}+\dfrac 1{\sqrt{k+1}}\right)>2(\sqrt{k+1}-\sqrt{k})\) ，推论是 \(T_n=\sum \dfrac 1{\sqrt i}\) ，\(2\sqrt n-\dfrac 32<T_n\leq 2\sqrt{n-1}\)

圆锥曲线

1. 圆锥曲线公式速查

   双曲线 ：\(c^2=a^2+b^2\)

   焦点为 \((-c,0),(c,0)\) ，方程为 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\) ，准线 \(x=\pm\dfrac{a^2}c\) ，渐近线 \(y=\pm\dfrac ba x\)

   焦点为 \((0,-c)(0,c)\) ，方程为 \(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\) ，准线 \(y=\pm\dfrac{a^2}c\) ，渐近线 \(y=\pm\dfrac abx\)

   顶点坐标 \((a,0)(-a,0)\)

   椭圆 ：（ \(b^2=a^2-c^2\) ），离心率 \(e=\dfrac ca\)

   焦点 \((-c,0),(c,0)\) ，方程为 \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)\)

   焦点 \((0,-c),(0,c)\) ，方程为 \(\dfrac{y^2}{a^2}+\dfrac{x^2}{b^2}=1(a>b>0)\)

   抛物线 ：

   右开口：\(y^2=2px\) ，焦点 \((\dfrac p2,0)\) ，准线 \(x=-\dfrac p2\) ，离心率 \(e=1\) ，\(x\ge 0\)

   左开口：\(y^2=-2px\) ，焦点 \((-\dfrac p2,0)\) ，准线 \(x=\dfrac p2\) ，离心率 \(e=1\) ，\(x\leq 0\)

   上开口：\(x^2=2py\) ，焦点 \((0,\dfrac p2)\) ，准线 \(y=-\dfrac p2\) ，离心率 \(e=1\) ，\(y\ge 0\)

   下开口：\(x^2=-2py\) ，焦点 \((0,-\dfrac p2)\) ，准线 \(y=\dfrac p2\) ，离心率 \(e=1\) ，\(y\leq 0\)

   切点 \((x_0,y_0)\) ：

   若 \(y^2=2px\) ，切线 \(y_0y=p(x_0+x)\) ；

   若 \(x^2=2py\) ，切线 \(x_0x=p(y_0+y)\) .

2. 抛物线准线上一点 \(P\) 作抛物线的两条切线，切点为 \(A,B\) ，\(AB\) 过焦点 \(F\) .

平面几何

1. 阿波罗尼斯圆：平面上两定点 \(A,B\) ，动点 \(P\) 满足 \(\dfrac{|PA|}{|PB|}=k(k\neq 1)\) ，\(P\) 的轨迹是一个以 \(k\) 内外分 \(AB\) 得到的两点为直径的圆。

   

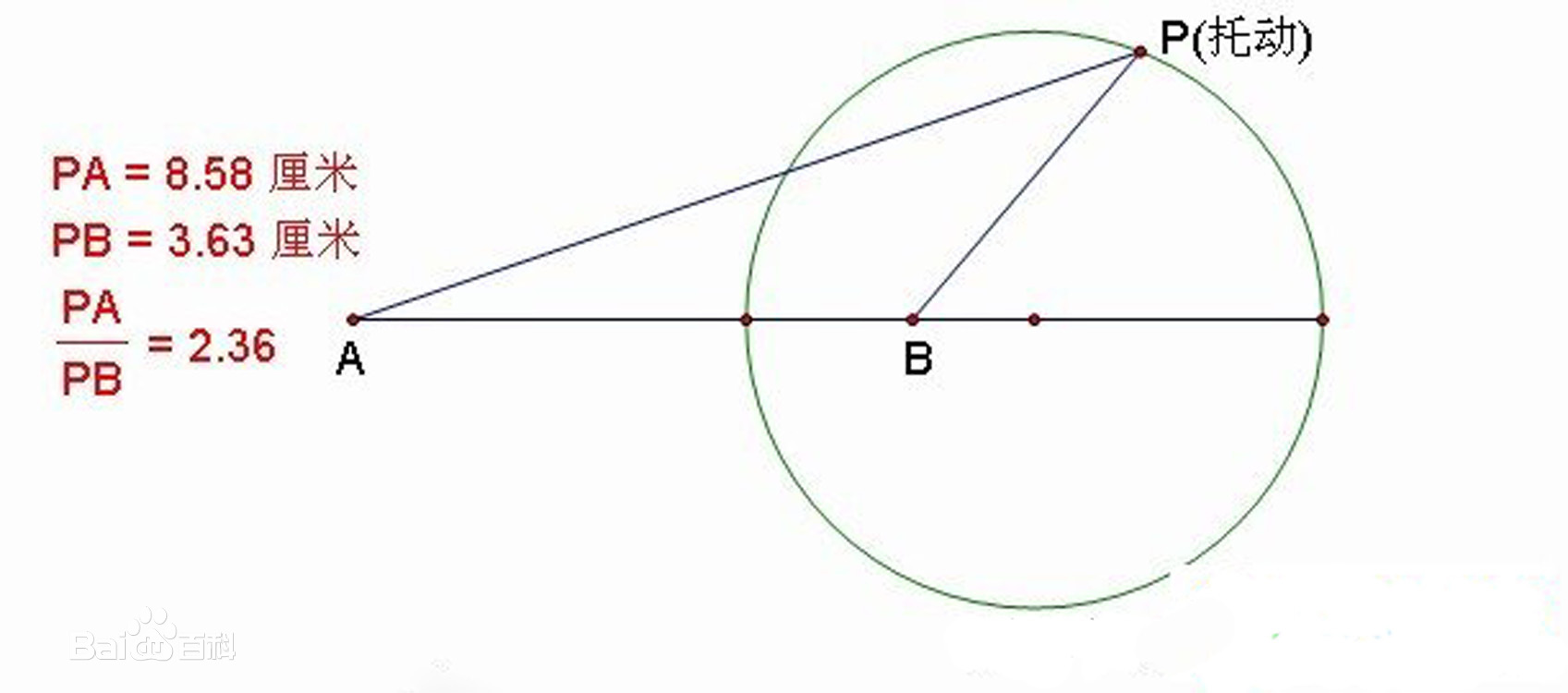
2. 点到直线距离公式：\(\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}\) .

3. 余弦定理： \(c^2=a^2+b^2-2ab\cos C,\cos C=\dfrac{a^2+b^2-c^2}{2ab}\) .

4. 正弦定理：\(\dfrac{a}{\sin A}=\cdots=2R\) .

立体几何

1. 空间角公式

   （1）异面直线所成角：\(a,b\) 为方向向量，\(\cos\theta=|\cos\left<a,b\right>|=\dfrac{|a\cdot b|}{|a||b|}\) .

   （2）线面角公式：\(a\) 为 \(l\) 的方向向量，\(n\) 为平面 \(\alpha\) 的法向量，\(\sin \theta=|\cos\left<a,n\right>|=\dfrac{|a\cdot n|}{|a|{{n}}}\) .

   （3）面面角公式：\(n_1,n_2\) 为法向量，\(\cos\left<n_1,n_2\right>=\dfrac{n_1\cdot n_2}{|n_1||n_2|}\) .

2. 线面角是最小的线线角。二面角是最大的线面角。

概率期望

• 方差：\(D(X)=\sum\limits_{i=1}^n[x_i-E(X)^2]p_i=E(X^2)-[E(X)]^2\) .

杂题

1. \(x+8y+8z=n,x,y,z\in N^*\) 有 \(666\) 组正整数解，求 \(n_{max}\)

   由于 \(x,y,z\) 都是正整数,因此 \(n=8k+a(0<a<8)\) 和 \(n=8k+8\) 的组数是一样多的\((x>=8)\)

   考虑 \((y,z)\) ,不妨设 \(y>=z\)
   \((y,z)=(1,1),(1,2)......(1,36)\)
   \((2,2),(2,3).......(2.35)\)
   \((3.3)................(3.34)\)
   \(.......\)
   \((18.18).(18,19)\)
   这样得到了 \(36+34+32+......+2=342\) 组解
   \((x,y,z)\) 解的个数就为 \(342\times 2-18\) (18为 \(y=z\) 的情形)= \(666\) 组，故 \(n=37\times 8+a(0<a<9)\) 均符合, \(304\) 最大。

英语

1. We tried to make the plane take off on time,but finally we couldn't compete with avoid the bad weather.

   把 compete 看成 complete 的奇怪错误

2. When you feel stressed stressful ,what do you usually do to make yourself relaxed?

   你做个人罢。

3. The moment she left the market,she found herself cheated cheating when dealing with the seller.

   没有好好看题……被动啊。

4. Nowadays a number of people know that going on such a diet can't keep in good shape.

   go on a diet 固定搭配，节食，减肥

5. Tag Questions 迷惑行为大赏

   Many girls dislike sports, don't they do ?

   We shouldn't pretend to know what we don't know, should shall we?

   Everybody in your family is an athlete, isn't doesn't he?

   Mary didn't lose any weight after going on a diet,did she? （是的，没减轻）

   • No Yes ,she didn't lose any weight.

   Don't lose heart if you meet some trouble,will you? （好的，我不会的）

   • No OK ,I won't.

6. There are five recognized kiwi species living alive today.

   alive 不能用在名词前面。

7. Until now,no one has have found an extinct giant parrot anywhere.

   nc错误。

8. 记录一些 词 & 词组。

   make up for ：弥补
   on hand ：在跟前，在旁边
   in rags ：衣衫褴褛
   ease/reduce/relieve the suffering we had seen
   march 行军走的步伐
   in circle 围成一圈
   exhausted 筋疲力尽
   examine 审查
   prevent 阻止
   dialog 会话，对话

9. A terrible flood happened in the village last week, Killing more than 20 people.

   结果状语：Killing more than 20 people

10. 省略 if 的虚拟条件句。

    Had my neighbor told me of the upcoming rainstorm with sympathy , I would have appreciated his warning.

    Had the Greyhound salesclerk sympathetically informed me that my bus had already left , I probably would have said , " Oh , that's all right. I'll catch the next one. "

11. thanks for 侧重原因，thanks to 侧重“多亏了某（对象）”

物理

1. 停在10层的电梯底板上放置有两块相同的条形磁铁，磁铁的极性如图所示，开始时两块磁铁在电梯底板上处于静止（　BC　BD ）

   

   A．若电梯突然向下开动（磁铁与底板始终相互接触），并停在1层，最后两块磁铁可能已碰在一起

   B．若电梯突然向下开动（磁铁与底板始终相互接触），并停在1层，最后两块磁铁一定仍在原来位置

   C．若电梯突然向上开动，并停在20层，最后两块磁铁可能已碰在一起

   D．若电梯突然向上开动，并停在20层最后两块磁铁一定仍在原来位置

   忽略了向上开动的时候还有减速的过程。

化学

生物

1. ATP的合成总是伴随着吸能反应的发生。（×）

   就 ATP 本身，断键吸能，成键放能，但是在 ATP 合成的时候（对于它本身是吸能），伴随着细胞里其他的放能反应 。

2. AMP即腺嘌呤核糖核苷酸，是RNA基本单位之一。

3. 动物细胞中，ATP合成中所需能量来源是呼吸作用中糖类等有机物氧化分解释放的能量。

4. 远离腺苷的高能磷酸键最容易断裂，如果题目表述是两个高能磷酸键最容易断裂且没有其他合适答案的话可以认为是错的。

5. 细胞内，通常一个吸能反应要伴随着一个放能反应。

6. 植物细胞内最重要的放能反应是糖的氧化。