AtCoder Grand Contest 017

比赛体验……之前做题的时候感觉 AtCoder 挺快的，现在打了VP之后发现还是会挂的……而且不是加载缓慢或者载不出来，直接给你一个无法访问，干脆利落。所以要打比赛的趁早把几道题都打开。

不过好消息是我发现我的垃圾英语水平看这个题面不成问题（顺便，如果需要翻译的话，GoldenDict 是真的好用

A - Biscuits

Description

There are $N$ bags of biscuits. The i-th bag contains $A_i$ biscuits.

Takaki will select some of these bags and eat all of the biscuits inside. Here, it is also possible to select all or none of the bags.

He would like to select bags so that the total number of biscuits inside is congruent to $P$ modulo $2$. How many such ways to select bags there are?

Solution

~~模数为2让我想到了模拟赛里没有用 bitset 的惨痛经历（~~

简单排列组合。分类讨论：

如果 $P=1$ ，那么每个 $\bmod 2=0$ 的 bag 可以随意选，反正对答案没有影响；对于 $\bmod 2=1$ 的，直接枚举选的个数（奇数个），然后算一下组合数 $C_n^i$ 即可。（其实为0的部分直接最后左移就好了）

如果 $P=0$ ，同理，不过是把奇数换成偶数而已。

由于题目对方案数并没有取模，但是处理阶乘又显然的炸了 unsigned long long ，于是只能暴力算组合数（就是一边乘一边除）。（这种诡异的求法我还想了一会儿……预处理做多了）

$1≤N≤50$
$P=0$ or $1$
$1≤A_i≤100$

Code

ull C( ull n,ull m )
{
    if ( m==0 ) return 1;
    ull res=1;
    for ( ull i=1; i<=n-m; i++ )
        res=res*(i+m)/i;
    return res;
}

int main()
{
    fac[0]=1;
    for ( int i=1; i<=50; i++ )
        fac[i]=fac[i-1]*i;

    scanf( "%d%d",&n,&P );
    for ( int i=1,x; i<=n; i++ )
        scanf( "%d",&x ),x&1 ? cnt1++ : cnt0++;
    ull ans=0;
    if ( P==0 )
    {
        for ( int i=0; i<=cnt1; i+=2 )
            ans+=C(cnt1,i);
        ans<<=cnt0;
    }
    else
    {
        for ( int i=1; i<=cnt1; i+=2 )
            ans+=C(cnt1,i);
        ans<<=cnt0;
    }
    printf( "%llu",ans );
}

B - Moderate Differences

Problem Link

Description

There are $N$ squares in a row. The leftmost square contains the integer $A$ , and the rightmost contains the integer $B$ . The other squares are empty.

Aohashi would like to fill the empty squares with integers so that the following condition is satisfied:

For any two adjacent squares, the (absolute) difference of the two integers in those squares is between $C$ and $D$ (inclusive).

As long as the condition is satisfied, it is allowed to use arbitrarily large or small integers to fill the squares. Determine whether it is possible to fill the squares under the condition.

$3≤N≤500000$
$0≤A≤10^9$
$0≤B≤10^9$
$0≤C≤D≤10^9$

Solution

很有意思的一道题目，写写不等式就是小学难度。

首先列出关于 $C,D$ 限制的式子： $\forall i\in[1,n),abs(x_{i+1}-x_i)\in[C,D]$ ，拆开绝对值得到：

\[C\leq x_{i+1}-x_i\leq D,or\ -D\leq x_{i+1}-x_i\leq -C. \]

然后考虑前后的 $A,B$ ，把所有 $x_{i+1}-x_i$ 求和得到： $\sum x_{i+1}-x_i=B-A$

考虑枚举属于 $[C,D]$ 和 $[-D,-C]$ 范围的个数，设后者为 $m$ ，那么根据上面的限制，把所有不等式相加，得到

\[C\times (n-m-1) +(-D)\times m\leq B-A\leq D\times (n-m-1)+(-C)\times m \]

暴力枚举 $m$ 求是否存在符合的 $m$ 即可。

Code

int main()
{
    ll n,m,a,b,c,d; cin>>n>>a>>b>>c>>d; bool fl=0;
    for ( m=1; m<=n; m++ )
        if ( c*(n-m-1)-d*m<=(b-a) && (b-a)<=(n-m-1)*d-c*m ) fl=1;
    fl ? printf( "YES\n" ) : printf( "NO\n" );
}

C - Snuke and Spells

Problem Link

Description

There are $N$ balls in a row. Initially, the i-th ball from the left has the integer $A_i$ written on it.

When Snuke cast a spell, the following happens:

Let the current number of balls be $k$ . All the balls with $k$ written on them disappear at the same time.

Snuke's objective is to vanish all the balls by casting the spell some number of times. This may not be possible as it is. If that is the case, he would like to modify the integers on the minimum number of balls to make his objective achievable.

By the way, the integers on these balls sometimes change by themselves. There will be $M$ such changes. In the j-th change, the integer on the $X_j$-th ball from the left will change into $Y_j$ .

After each change, find the minimum number of modifications of integers on the balls Snuke needs to make if he wishes to achieve his objective before the next change occurs. We will assume that he is quick enough in modifying integers. Here, note that he does not actually perform those necessary modifications and leaves them as they are.

$1≤N≤200000$
$1≤M≤200000$
$1≤A_i≤N$
$1≤X_j≤N$
$1≤Y_j≤N$

Solution

考虑数轴上的 $N$ 个坐标 $1\sim N$ ，每个都挂有绳索，长度为 $0$ .对于每个颜色为 $A_i=k$ 的球，在 $k$ 坐标上绳子长度加一。最后把所有绳子往数轴负方向拉直。如果绳子覆盖了 $[0,N]$ 那么一定可以做到。否则未被覆盖的总长度就是答案。

考虑如何证明这个结论。

首先如果全覆盖了，那么就不需要改变。

如果没有覆盖，那么需要把一个球的编号 $i$ 改成 $j$ ，这样标号 $i$ 的线段长度减少一格，标号为 $j$ 的增加一格，每次最多减少一个没被覆盖的区间，所以答案就是没覆盖的区间长度。至于为什么可以改，很简单，因为总数是 $N$ ，如果有没覆盖的一定是有重叠的，那么把重叠的贡献用来填补没覆盖的就好了。

Code

void add( int x )
{
    if ( x<=0 ) return;
    if ( ++cov[x]==1 ) ans++;
}

void dec( int x )
{
    if ( x<=0 ) return;
    if ( --cov[x]==0 ) ans--;
}

int main()
{
    scanf( "%d%d",&n,&m );
    for ( int i=1; i<=n; i++ )
    {
        scanf( "%d",&a[i] ); num[a[i]]++;
        add( a[i]-num[a[i]]+1 );
    }
    while ( m-- )
    {
        int x,y; scanf( "%d%d",&x,&y );

        dec( a[x]-num[a[x]]+1 );
        num[a[x]]--; num[y]++;
        add( y-num[y]+1 ); a[x]=y;

        printf( "%d\n",n-ans );
    }
}

D - Game on Tree

Problem Link

Description

There is a tree with $N$ vertices numbered $1,2,...,N$ . The edges of the tree are denoted by $(x_i,y_i)$ .

On this tree, Alice and Bob play a game against each other. Starting from Alice, they alternately perform the following operation:

Select an existing edge and remove it from the tree, disconnecting it into two separate connected components. Then, remove the component that does not contain Vertex $1$ .

A player loses the game when he/she is unable to perform the operation. Determine the winner of the game assuming that both players play optimally.

$2≤N≤100000$
$1≤x_i,y_i≤N$

Solution

对于 Official Editorial 的一点解释：Grundy Number 就是 SG函数值。SG函数这个东西是 Sprague-Grundy 定理搞出来的。

考虑根节点只有一个孩子的情况。显然把这条边断掉就是 Alice 赢了，SG 函数为 1.

如果有 $k$ 棵子树，那么可以分成独立的 $k$ 个游戏，SG 函数值为异或和。

如果只有一棵子树，分情况讨论：

如果断开了根和子树相连的边，那么下一状态 SG 值为0；
否则，在子树的 SG 函数集合中，$0+1,1+1,...,SG(rt)-1+1$ 会出现，但 $SG(rt)+1$ 不会，那么原树的 SG 值就是子树的 SG 值加一。

所以可以对这棵树 DFS，一棵树的 SG 值就是子树 SG 值加一之后的异或和。

Code

int dfs( int u,int fa )
{
    int res=0;
    for ( int i=head[u]; i; i=e[i].nxt )
        if ( e[i].to!=fa ) res^=dfs( e[i].to,u )+1;
    return res;
}

E - Jigsaw

Problem Link

Description

We have $N$ irregular jigsaw pieces. Each piece is composed of three rectangular parts of width $1$ and various heights joined together. More specifically:

The i-th piece is a part of height $H$ , with another part of height $A_i$ joined to the left, and yet another part of height $B_i$ joined to the right, as shown below. Here, the bottom sides of the left and right parts are respectively at $C_i$ and $D_i$ units length above the bottom side of the center part.

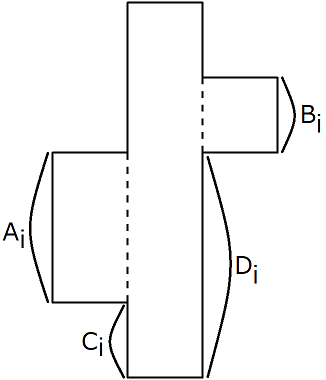
Snuke is arranging these pieces on a square table of side 10100. Here, the following conditions must be held:

All pieces must be put on the table.
The entire bottom side of the center part of each piece must touch the front side of the table.
The entire bottom side of the non-center parts of each piece must either touch the front side of the table, or touch the top side of a part of some other piece.
The pieces must not be rotated or flipped.

Determine whether such an arrangement is possible.

$1≤N≤100000$
$1≤H≤200$
$1≤Ai≤H$
$1≤Bi≤H$
$0≤Ci≤H−A_i$
$0≤Di≤H−B_i$

Solution

定义第 $i$ 块的类型为：

如果 $C_i=0,l=+A_i$ , 否则 $l=-C_i$
如果 $D_i=0,r=-B_i$ ，否则 $r=+B_i$
第 $i$ 块的类型定义为 $(l,r)$

对于拼图 $(l',r')$ ，它能被放在 $(l,r)$ 右边需要满足以下条件之一：

$l>0 ,r<0 $
$r=l'$

同时，当你安排所有拼图的时候，最左边的一块的 $l$ 必须是正的，最右边的一块的 $r$ 必须是负的。

现在，构造一张包含 $2H$ 个点的有向图，这些点被标号为 $1,2,..,H,-1,-2,...,-H.$ 对于每一块 $(l,r)$ 的拼图，从 $l$ 到 $r$ 加一条边。

根据上述构造，我们需要确定是否可以把这张图分成几条路径，每一条从一个正点开始，在一个负点结束。对于每个点，要么被经过，出入度都++，要么作为起点或终点，只增加入度或者出度。

这个判定问题与下面这些条件是等价的：

对于每个正点，出度不小于入度
对于每个负点，出度不大于入度
每个连通块中，有至少一个点的出度和入度不同（必须有起点和终点）

按这个条件并查集判定就好了。

Code

int main()
{
    n=read(); m=read();
    for ( int i=1; i<=m; i++ )
        fa[i]=i,fa[i+m]=i+m,vis[i]=vis[i+m]=0;
    for ( int i=1; i<=n; i++ )
    {
        int a=read(),b=read(),c=read(),d=read();
        int l1=c>0 ? -c : a,r1= d>0 ? d : -b;
        l1+=m; r1+=m; 
        if ( find(l1)!=find(r1) ) fa[find(l1)]=find(r1);
        ind[r1]++; oud[l1]++;
    }

    for ( int i=0; i<m; i++ )
        if ( oud[i]>ind[i] ) { printf( "NO" ); return 0; }
    for ( int i=m+1; i<=m+m; i++ )
        if ( oud[i]<ind[i] ) { printf( "NO" ); return 0; }
    for ( int i=0; i<=m+m; i++ )
        if ( ind[i]!=oud[i] ) vis[find(i)]=1;
    for ( int i=0; i<=m+m; i++ )
        if ( ind[i] && oud[i] && !vis[find(i)] ) { printf( "NO" ); return 0; }
    printf( "YES" );
}

F - Zigzag

Problem Link

Description

There are $N(N+1)/2$ dots arranged to form an equilateral triangle whose sides consist of $N$ dots, as shown below. The j-th dot from the left in the i-th row from the top is denoted by $(i,j)$ $(1≤i≤N, 1≤j≤i)$ . Also, we will call $(i+1,j)$ immediately lower-left to $(i,j)$ , and $(i+1,j+1)$ immediately lower-right to $(i,j)$ .

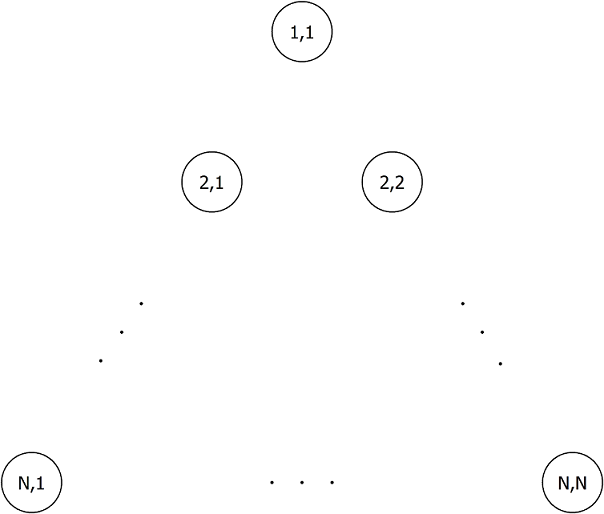
Takahashi is drawing $M$ polygonal lines $L_1,L_2,...,L_M$ by connecting these dots. Each $L_i$ starts at $(1,1)$ , and visits the dot that is immediately lower-left or lower-right to the current dots $N−1$ times. More formally, there exist $X_{i,1},...,X_{i,N}$ such that:

$L_i$ connects the $N$ points $(1,X_{i,1}),(2,X_{i,2}),...,(N,X_{i,N})$ , in this order.
For each $j=1,2,...,N−1$ , either $X_{i,j+1}=X_{i,j}$ or $X_{i,j+1}=X_{i,j+1}$ holds.

Takahashi would like to draw these lines so that no part of $L_i+1$ is to the left of $L_i$ . That is, for each $j=1,2,...,N$ $X_{1,j}≤X_{2,j}≤...≤X_{M,j} $, must hold.

Additionally, there are $K$ conditions on the shape of the lines that must be followed. The i-th condition is denoted by $(A_i,B_i,C_i)$ , which means:

If $C_i=0$ , $L_{A_i}$ must visit the immediately lower-left dot for the $B_i$-th move.
If $C_i=1$ , $L_{A_i}$ must visit the immediately lower-right dot for the $B_i$-th move.

That is, $X_{A_i,B_i+1}=X_{A_i,B_i+C_i}$ must hold.

In how many ways can Takahashi draw MM polygonal lines? Find the count modulo $1000000007$ .

题面过长，这里提供 luogu 的翻译版本：

给定一个 N 层的三角形图，第 $i$ 层有 $i$ 个节点。

第 $i$ 层的节点，从左到右依次标号为 $(i, 1), (i, 2),... , (i, i)$ 。

你需要从 $(1,1)$ 往下画 $M$ 条折线。

对于每条折线的每一个小段，你可以从 $(i, j)$ 画到 $(i + 1, j)$ 或者 $(i + 1, j + 1)$ 。

同时你还必须保证第 $i$ 条折线的任何一个位置必须不能处在第 $i - 1$ 条折线的左侧，它们必须按照从左到右的顺序排列。

有 $K$ 条限制，每条限制形如 $(A_i, B_i, C_i)$ .

表示第 $A_i$ 条折线处于位置 $(B_i, j)$ 时，下一小段必须走向 $(B_i + 1, j + C_i)$ ，也就是当 $C_i = 0$ 时向左，当 $C_i = 1$ 时向右。

询问不同的折线画法的方案数，对 ${10}^9 + 7$ 取模。

Solution

最直接的想法是暴力状压 DP ，枚举状态转移，复杂度 $O(m4^n)$ . 这样显然处理了很多不合法情况，考虑优化。

设 $0$ 为向左走, $1$ 为向右走，不考虑方向限制，合法转移后的状态一定是满足任何一个前缀 1 的个数都要大于之前状态前缀 1 的个数。

设 $d p [ i ] [ j ] [ k ]$ 表示考虑到第 $i$ 条路径的第 $j$ 次转移，目前能走的最左侧的路线是 $k$ .

枚举下一步往哪里走。

如果向左走，那么当前状态的这个位置必须为0，否则不合法。

如果向右走，且当前状态的这一位为 1，直接走即可。否则就把后面的一个 1 挪到这里， $O(1)$ 转移。

Code

int main()
{
	n=read()-1; m=read(); k=read();
	for ( int i=1; i<=k; i++ )
	{
		int x=read(),y=read(),z=read();
		mp[x][y-1]=z+1;
	}

	f[0][0]=1; int now=0;
	for ( int i=1; i<=m; i++ )
	 for ( int j=0; j<n; j++ )
	 {
		now^=1; memset( f[now],0,sizeof(f[now]) );
		for ( int s=0; s<(1<<n); s++ )
			if ( f[now^1][s] )
			{
				if ( mp[i][j]!=2 && ((s>>j)&1)==0 ) f[now][s]=(f[now][s]+f[now^1][s])%mod;
				//可以向左，而且只能向左
				if ( mp[i][j]!=1 )	//可以向右
				{
					int nxt=0;
					if ( (s>>j)&1 ) nxt=s;		//本来就是1，直接填
					else		//把下一个1挪上来
					{
						int tmp=((-1)^((1<<(j+1))-1))&s,t2= tmp ? lowbit(tmp) : 0;
						nxt=s^(1<<j)^t2;
					}
					f[now][nxt]=(f[now][nxt]+f[now^1][s])%mod;
				}
			}
	 }

	int ans=0;
	for ( int s=0; s<(1<<n); s++ )
	 	ans=(ans+f[now][s])%mod;
	printf( "%d\n",ans );
}

Last

感觉自己好菜啊……思维和手速都不大行/kk

看来还是要多打这种题，不然脑子不好使。

有一说一，感觉 AtCoder 的题比 CF 质量高一点（可能也是因此比赛比较少吧）。挺喜欢这样的纯思维场的。~~顺便练习英语/cy~~

posted @ 2020-11-11 16:59 MontesquieuE 阅读(139) 评论(0) 编辑收藏举报

刷新页面返回顶部

Amaurëa.

AtCoder Grand Contest 017

A - Biscuits

Description

Solution

Code

B - Moderate Differences

Description

Solution

Code

C - Snuke and Spells

Description

Solution

Code

D - Game on Tree

Description

Solution

Code

E - Jigsaw

Description

Solution

Code

F - Zigzag

Description

Solution

Code

Last

公告