基础DP（1）

硬币问题

 

n种硬币，面值v1，v2...vn，数量无限，输入s，使最少的硬币组合之和为s。（贪心解决的硬币问题使特殊面值，此处面对任意面值）

 

Min[i]是金额i对应的最少硬币数量，易得Min[i]=min(Min[i]，Min[i-1]+1)。（如果面值是1的话）

 

从Min[i-1]到Min[i]的递推称为状态转移。

 

代码如下（最小硬币的组合）：

#include<bits/stdc++.h>
using namespace std;
const int MONEY=251;
const int VALUE=5;
int type[VALUE]={1,5,10,25,50};
int Min[MONEY];
void solve(){
    for(int k=0;k<MONEY;k++){
        Min[k]=INT_MAX;
    }
    Min[0]=0;
    for(int j=0;j<VALUE;j++){
        for(int i=type[j];i<MONEY;i++){
            Min[i]=min(Min[i],Min[i-type[j]]+1);
        }
    }
}
int main()
{
    int s;
    solve();
    while(~scanf("%d",&s)){
        printf("%d\n",Min[s]);
    }
    return 0;
}

 

http://acm.hdu.edu.cn/showproblem.php?pid=2069

 

这个是所有硬币组合。

 

 

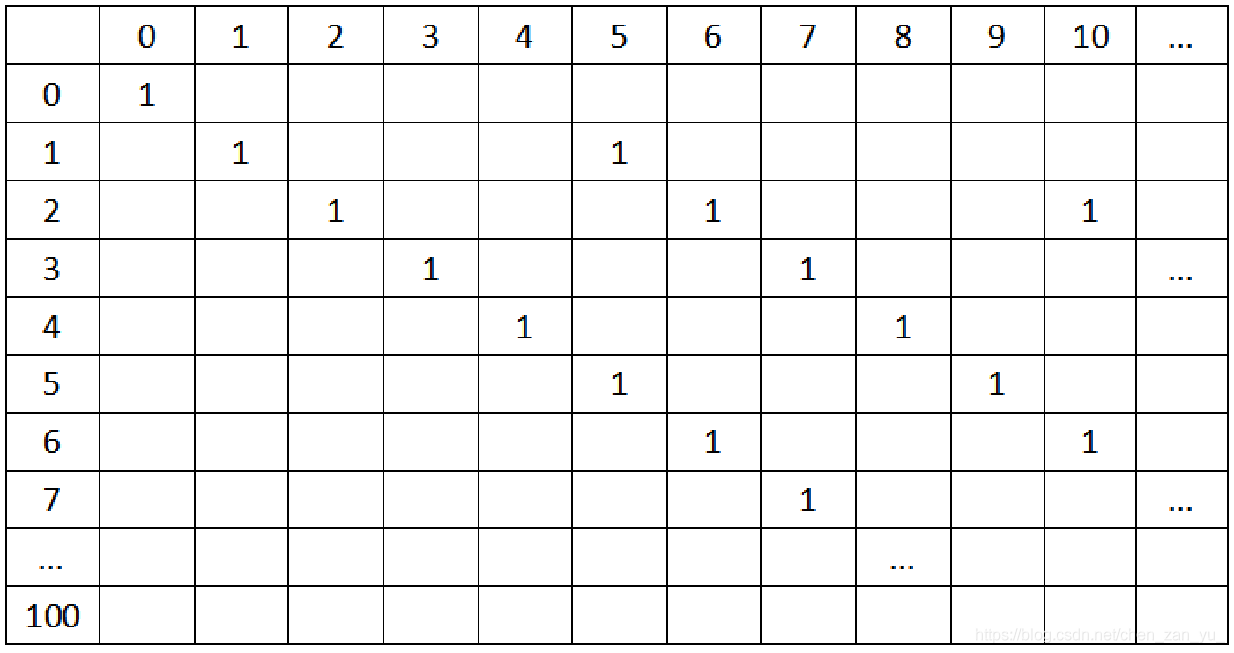
如图，表中纵坐标相加就是某金额对应的方案总数，状态转移的特征是用矩阵前面的状态dp[i][j]能推算出后面状态的值。

 

代码：

#include<bits/stdc++.h>
using namespace std;
const int COIN = 101;                   //题目要求不超过100个硬币
const int MONEY = 251;                  //题目给定的钱数不超过250
int dp[MONEY][COIN] = {0};              // DP转移矩阵
int type[5] = {1, 5, 10, 25, 50};      //5种面值
void solve() {                             // DP
    dp[0][0] = 1;
    for(int i=0; i<5; i++)
        for(int j=1; j<COIN; j++)
            for(int k = type[i]; k < MONEY; k++)
                dp[k][j] += dp[k-type[i]][j-1];
}
int main() {
    int s;
    int ans[MONEY] = {0};
    solve();                          //用DP计算完整的转移矩阵
    for(int i=0; i< MONEY; i++)   //对每个金额，计算有多少种组合方案。打表
        for(int j=0; j<COIN; j++)  //从0开始，注意 dp[0][0]=1
            ans[i] += dp[i][j];
    while(cin >> s)
        cout << ans[s] << endl;
    return 0;
}

 

（ps：感谢某本书提供的代码，下次一定补上自己写的）